Class 11 NCERT Solutions- Chapter 15 Statistics – Exercise 15.2

Find the mean and variance for each of the data in Exercise 1 to 5.

Question 1. 6, 7, 10, 12, 13, 4, 8, 12

Solution:

We know,
$Mean = \frac{Sum \space of \space total \space observations}{No.\space of\space obervations} \\ = \frac{\sum_{i=1}^{a}x_i}{n}$
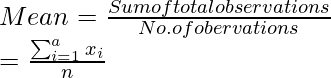
So, 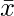$\bar{x}$ = (6 + 7 + 10 + 12 + 13 + 4 + 8 + 12)/8
= 72/8
= 9
x_i
Deviations from mean
(x_i– x’)
(xi – x’)²
6 6 – 9 = -3 9
7 7 – 9 = -2 4
10 10 – 9 = 1 1
12 12 – 9 = 3 9
13 13 – 9 = 4 16
4 4 – 9 = – 5 25
8 8 – 9 = – 1 1
12 12 – 9 = 3 9
74
$\sigma^2 = \frac{1}{n}\sum_{i=1}^{a}(x_i-\overline{x})^2$
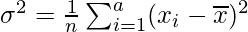
σ²= (1/8) × 74
= 9.2
Therefore, Mean = 9 and Variance = 9.25

Question 2. First n natural numbers

Solution:

$Mean = \frac{Sum \space of \space total \space observations}{No.\space of\space obervations} \\ = \frac{\sum_{i=1}^{a}x_i}{n}$
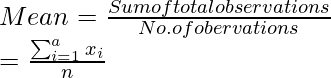
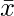$\bar{x}$ = ((n(n + 1))2)/n
= (n + 1)/2
$\sigma^2 = \frac{1}{n}\sum_{i=1}^{a}(x_i-\overline{x})^2$
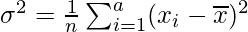
On substituting the value of mean,
$= \frac{1}{n}\sum_{i=1}^{n}(x_i - \frac{n+1}{2})^2 \\ = \frac{1}{n}\sum_{i=1}^{n}(x_i)^2 - \frac{1}{n}\sum_{i=1}^{n}2x_i(\frac{n+1}{2})+\frac{1}{n}\sum_{i=1}^{n}(\frac{n+1}{2})^2$
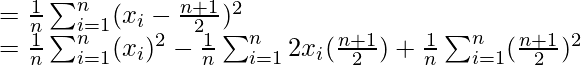Substituting values of Summation
$\\ = \frac{1}{n}\frac{n(n+1)(2n+1)}{6}-\frac{n+1}{n}[\frac{n(n+1)}{2}]+\frac{(n+1)^2}{4n}×n$
On extracting common values, we have,
$= (n+1)[\frac{4n+2-3n-3}{12}] \\ = \frac{(n+1)(n-1)}{12}$
σ² = (n² – 1)/12
Mean = (n + 1)/2 and Variance = (n² – 1)/12

Question 3. First 10 multiples of 3

Solution:

The required multiples of 3 are 3, 6, 9, 12, 15, 18, 21, 24, 27, 30.
We know,
$Mean = \frac{Sum \space of \space total \space observations}{No.\space of\space obervations} \\ = \frac{\sum_{i=1}^{a}x_i}{n}$
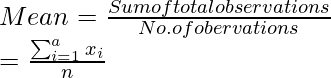
So, 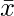$\bar{x}$ = (3 + 6 + 9 + 12 + 15 + 18 + 21 + 24 + 27 + 30)/10
= 165/10
= 16.5
x_i
Deviations from mean
(x_i– x’)
(x_i – x’)²
3 3 – 16.5 = -13.5 182.25
6 6 – 16.5 = -10.5 110.25
9 9 – 16.5 = -7.5 56.25
12 12 – 16.5 = -4.5 20.25
15 15 – 16.5 = -1.5 2.25
18 18 – 16.5 = 1.5 2.25
21 21 – 16.5 = – 4.5 20.25
24 24 – 16.5 = 7.5 56.25
27 27 – 16.5 = 10.5 110.25
30 30 – 16.5 = 13.5 182.25
742.5
$\sigma^2 = \frac{1}{n}\sum_{i=1}^{a}(x_i-\overline{x})^2$
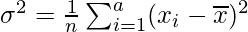
= (1/10) × 742.5
= 74.25
Therefore, Mean = 16.5 and Variance = 74.25

Question 4.

x_i	6	10	14	18	24	28	30
f_i	2	4	7	12	8	4	3

Solution:

x_i	f_i	f_ix_i	x_i – x’	(x_i – x’)²	f_i(x_i– x’)²
6	2	12	6 – 19 = 13	169	338
10	4	40	10-19 = -9	81	324
14	7	98	14-19 = -5	25	175
18	12	216	18-19 = -1	1	12
24	8	192	24-19 = 5	25	200
28	4	112	28-19 = 9	81	324
30	3	90	30-19 = 11	121	363
					1736

$Mean = \frac{Sum \space of \space total \space observations}{No.\space of\space obervations} \\ = \frac{\sum_{i=1}^{a}x_i}{n}$
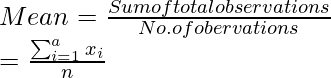
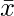$\bar{x}$ = 760/40
= 19
Also,
$\sigma^2 = \frac{1}{n}\sum_{i=1}^{a}(x_i-\overline{x})^2$
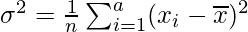
= (1/40) × 1736
= 43.4

Question 5.

x_i	92	93	97	98	102	104	109
f_i	3	2	3	2	6	3	3

Solution:

x_i	f_i	f_ix_i	x_i– x’	(x_i – x’)²	f_i(x_i – x’)²
92	3	276	92-100 = -8	64	192
93	2	186	93-100 = -7	49	98
97	3	291	97-100 = -3	9	27
98	2	196	98-100 = -2	4	8
102	6	612	102-100 = 2	4	24
104	3	312	104-100 =4	16	48
109	3	327	109-100 = 9	81	243
	N = 22	2200			640

$Mean = \frac{Sum \space of \space total \space observations}{No.\space of\space obervations} \\ = \frac{\sum_{i=1}^{a}x_i}{n}$
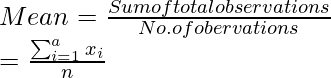
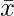$\bar{x}$ = 2200/22
= 100
$\sigma^2 = \frac{1}{n}\sum_{i=1}^{a}(x_i-\overline{x})^2$
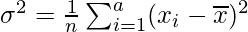
= (1/22) × 640
= 29.09
Therefore, Mean = 100 and Variance = 29.09

Question 6. Find the mean and standard deviation using short-cut method.

x_i	60	61	62	63	64	65	66	67	68
f_i	2	1	12	29	25	12	10	4	5

Solution:

$\overline X = A + \frac{\sum_{i=1}^{a}f_iy_i}{N} × h$
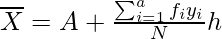
Where A = 64, h = 1
So, 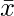$\bar{x}$ = 64 + ((0/100) × 1)
= 64 + 0
= 64
Then, variance,
$\sigma^2 = \frac{h^2}{N^2}[N\sum f_iy_i^2 - (\sum f_iy_i)^2]$
σ² = (1²/100²) [100(286) – 0²]
= (1/10000) [28600 – 0]
= 28600/10000
= 2.86
Hence, standard deviation = σ = √2.886
= 1.691
Therefore,
Mean = 64 and Standard Deviation = 1.691

Question 7.

Classes	0-30	30-60	60-90	90-120	120-150	150-180	180-210
Frequencies	2	3	5	10	3	5	2

Solution:

Classes	f_i	x_i	f_ix_i	(x_i– x’)	(xi – x’)²	f_i(xi – x’)²
0-30	2	15	30	-92	8464	16928
30-60	3	45	135	-62	3844	11532
60-90	5	75	375	-32	1024	5120
90-120	10	105	1050	-2	4	40
120-150	3	135	405	28	784	2352
150-180	5	165	825	58	3364	16820
180-210	2	195	390	88	7744	15488
	N = 30		3210			68280

$Mean = \frac{Sum \space of \space total \space observations}{No.\space of\space obervations} \\ = \frac{\sum_{i=1}^{a}x_i}{n}$
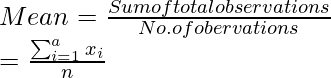
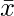$\bar{x}$ = 3210/30
= 107
$\sigma^2 = \frac{1}{n}\sum_{i=1}^{a}(x_i-\overline{x})^2$
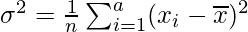
= (1/30) × 68280
= 2276
Therefore, Mean = 107 and Variance = 2276

Question 8.

Classes	0-10	10-20	20-30	30-40	40-50
Frequencies	5	8	15	16	6

Solution:

Classes	f_i	x_i	f_ix_i	(x_i-x’)	(x_i-x’)²	f_i(x_i-x’)²
0-10	5	5	25	-22	484	2420
10-20	8	15	120	-12	144	1152
20-30	15	25	375	-2	4	60
30-40	16	35	560	8	64	1024
40-50	6	45	270	18	324	1944
	N = 50		1350			6600

$Mean = \frac{Sum \space of \space total \space observations}{No.\space of\space obervations} \\ = \frac{\sum_{i=1}^{a}x_i}{n}$
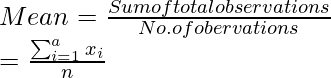
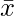$\bar{x}$ = 1350/50
= 27
$\sigma^2 = \frac{1}{n}\sum_{i=1}^{a}(x_i-\overline{x})^2$
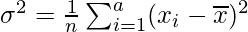
= (1/50) × 6600
= 132
Therefore, Mean = 27 and Variance = 132

Question 9. Find the mean, variance and standard deviation using short-cut method

Heights in cms	70-75	75-80	80-85	85-90	90-95	95-100	100-105	105-110	110-115
Frequencies	3	4	7	7	15	9	6	6	3

Solution:

Height	f_i	X_i	Y_{i =}(X_i-A)/h	Y_i²	f_iy_i	f_iy_i²
70-75	2	72.5	-4	19	-12	48
75-80	1	77.5	-3	9	-12	36
80-85	12	82.5	-2	4	-14	28
85-90	29	87.5	-1	1	-7	7
90-95	25	92.5	0	0	0	0
95-100	12	97.5	1	1	9	9
100-105	10	102.5	2	4	12	24
105-110	4	107.5	3	9	18	54
110-115	5	112.5	4	16	12	48
115-120	N = 60				6	254

$\overline X = A + \frac{\sum_{i=1}^{a}f_iy_i}{N} × h$
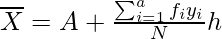
Where, A = 92.5, h = 5
So, 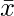$\bar{x}$ = 92.5 + ((6/60) × 5)
= 92.5 + 0.5
= 92.5 + 0.5
= 93
Then, Variance,
$\sigma^2 = \frac{h^2}{N^2}[N\sum f_iy_i^2 - (\sum f_iy_i)^2]$
Standard deviation = σ = √105.583
= 10.275

Question 10. The diameters of circles (in mm) drawn in a design are given below:

Diameters	33-36	37-40	41-44	45-48	49-52
No. of circles	15	17	21	22	25

Calculate the standard deviation and mean diameter of the circles.

[Hint first make the data continuous by making the classes as 32.5-36.5, 36.5-40.5, 40.5-44.5, 44.5 – 48.5, 48.5 – 52.5 and then proceed.]

Solution:

Height	f_i	x_i	Y_i = (X_i-A)/h	Y_i²	f_iy_i	fiyi²
32.5-36.5	15	34.5	-2	4	-30	60
36.5-40.5	17	38.5	-1	1	-17	17
40.5-44.5	21	42.5	0	0	0	0
44.5-48.5	22	46.5	1	1	22	22
48.5-52.5	25	50.5	2	4	50	100
	N=100				25	199

$\overline X = A + \frac{\sum_{i=1}^{a}f_iy_i}{N} × h$
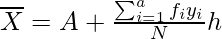
Where, A = 42.5, h = 4
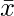$\bar{x}$ = 42.5 + (25/100) × 4
= 42.5 + 1
= 43.5
Then, Variance,
$\sigma^2 = \frac{h^2}{N^2}[N\sum f_iy_i^2 - (\sum f_iy_i)^2]$
σ² = (4²/100²)[100(199) – 25²]
On solving, we get,
= (1/625) [19900 – 625]
= 19275/625
= 771/25
= 30.84
Hence, standard deviation = σ = √30.84
= 5.553

Last Updated : 25 Feb, 2021

x_i	Deviations from mean (x_i– x’)	(xi – x’)²
6	6 – 9 = -3	9
7	7 – 9 = -2	4
10	10 – 9 = 1	1
12	12 – 9 = 3	9
13	13 – 9 = 4	16
4	4 – 9 = – 5	25
8	8 – 9 = – 1	1
12	12 – 9 = 3	9
		74

Chapter 1: Sets

Chapter 2: Relations and Functions

Chapter 3: Trigonometric Functions

Chapter 4: Principle of Mathematical Induction

Chapter 5: Complex Numbers and Quadratic Equations

Chapter 6: Linear Inequalities

Chapter 7: Permutations and Combinations

Chapter 8: Binomial Theorem

Chapter 9: Sequences and Series

Chapter 10: Straight Lines

Chapter 11: Conic Sections

Chapter 12: Introduction to Three-dimensional Geometry

Chapter 13: Limits and Derivatives

Chapter 14: Mathematical Reasoning

Chapter 15: Statistics

Chapter 16: Probability

Chapter 1: Sets

Chapter 2: Relations and Functions

Chapter 3: Trigonometric Functions

Chapter 4: Principle of Mathematical Induction

Chapter 5: Complex Numbers and Quadratic Equations

Chapter 6: Linear Inequalities

Chapter 7: Permutations and Combinations

Chapter 8: Binomial Theorem

Chapter 9: Sequences and Series

Chapter 10: Straight Lines

Chapter 11: Conic Sections

Chapter 12: Introduction to Three-dimensional Geometry

Chapter 13: Limits and Derivatives

Chapter 14: Mathematical Reasoning

Chapter 15: Statistics

Chapter 16: Probability

Class 11 NCERT Solutions- Chapter 15 Statistics – Exercise 15.2

Find the mean and variance for each of the data in Exercise 1 to 5.

Question 1. 6, 7, 10, 12, 13, 4, 8, 12

Question 2. First n natural numbers

Question 3. First 10 multiples of 3

Question 4.

Question 5.

Question 6. Find the mean and standard deviation using short-cut method.

Question 7.

Question 8.

Question 9. Find the mean, variance and standard deviation using short-cut method

Question 10. The diameters of circles (in mm) drawn in a design are given below:

Calculate the standard deviation and mean diameter of the circles.

[Hint first make the data continuous by making the classes as 32.5-36.5, 36.5-40.5, 40.5-44.5, 44.5 – 48.5, 48.5 – 52.5 and then proceed.]

Please Login to comment...