GeeksforGeeks brings a Formula sheet for Class 11 Maths students, which is strictly based on the NCERT Syllabus to ease out the preparation and revision process of the students for school exams as well as various competitive exams like JEE and NEET. This article not only includes the list of formulae but offer students a summary of the chapters, important points to remember, a brief explanation of important concepts and derivations of formulae for better comprehension and retaining of the chapters. Hence, these Chapter-wise CBSE Class 11 Maths Formulae are prepared to ensure maximum preparation and good marks in any examination.

Chapter 1: Sets
The chapter explains the concept of sets along with their representation. The topics discussed are empty sets, equal sets, subsets, finite and infinite sets, power sets, and universal sets. A set is a well-collaborated collection of objects. A set consisting of definite elements is a finite set. Otherwise, it is an infinite set. Below are the important terms and properties used in Sets are listed as:
- The union of two sets A and B are said to be contained elements that are either in set A and set B. The union of A and B is denoted as, A∪B.
- The intersection of two sets A and B are said to be contained elements that are common in both sets. The intersection of A and B is denoted as, A∩B.
- The complement of a set A is the set of all elements given in the universal set U that are not contained in A. The complement of A is denoted as, A’.
- For any two sets A and B, the following holds true:(DE Morgan’s Theorem)
- If the finite sets A and B are given such that, (A∩B)=ϕ, then:
n(A∪B)=n(A)+n(B)
n(A∪B)=n(A)+n(B)−n(A∩B)
- Some other important formulas of Sets for any three sets A, B, and C are as follows:
- A – A = Ø
- B – A = B⋂ A’
- B – A = B – (A⋂B)
- (A – B) = A if A⋂B = Ø
- (A – B) ⋂ C = (A⋂ C) – (B⋂C)
- A ΔB = (A-B) U (B- A)
- n(A∪B) = n(A) + n(B) – n(A⋂B)
- n(A∪B∪C)= n(A) +n(B) + n(C) – n(B⋂C) – n (A⋂ B)- n (A⋂C) + n(A⋂B⋂C)
- n(A – B) = n(A∪B) – n(B)
- n(A – B) = n(A) – n(A⋂B)
- n(A’) = n(∪) – n(A)
- n(U) = n(A) + n(B) + – n(A⋂B) + n((A∪B)’)
- n((A∪B)’) = n(U) + n(A⋂B) – n(A) – n(B)
Chapter 2: Relations & Functions
The chapter Relations & Functions explains the advanced concepts of sets theory using the concept of ordered and unordered pairs of elements. An ordered pair is a pair of elements grouped together in a certain order. A relation R towards a set A to a set B can be described as a subset of the cartesian product A × B which is obtained by describing a relationship between the first of its element x and the second of its element y given in the ordered pairs of A × B.
The below-mentioned properties will surely assist students to solve various maths problems:
- Relations: A relation R is the subset of the cartesian product of A × B, where A and B are two non-empty elements. It is derived by stating the relationship between the first element and second element of the ordered pair of A × B.
- Inverse of Relation: A and B are any two non-empty sets. Let R be a relationship between two sets A and B. The inverse of relation R, indicated as R-1, is a relationship that connects B and A and is defined by
R-1 ={(b, a) : (a, b) ∈ R}
where, Domain of R = Range of R-1 and Range of R = Domain of R-1.
- Functions: A relation f from a set A to set B is said to be function, if every element of set A has one and only image in set B.
- A cartesian product A × B of two sets A and B is given by: A × B = { (a,b) : a ϵ A, b ϵ B}
- If (a, b) = (x, y); then a = x and b = y
- If n(A) = x and n(B) = y, then n(A × B) = xy and A × ϕϕ = ϕϕ
- The cartesian product: A × B ≠ B × A.
- A function f from set A to set B considers a specific relation type where every element x in set A has one and only one image in set B. A function can be denoted as f : A → B, where f(x) = y.
- Algebra of functions: If the function f : X → R and g : X → R; we have:
- (f + g)(x) = f(x) + g(x) ; x ϵ X
- (f – g)(x) = f(x) – g(x)
- (f . g)(x) = f(x).g(x)
- (kf)(x) = k(f(x)) where k is a real number
- {f/g}(x) = f(x)/g(x), g(x)≠0
Chapter 3: Trigonometric Functions
In Mathematics, trigonometric functions are the real functions that relate to an angle of a right-angled triangle forming some finite ratios of two side lengths. Find the important Maths formulas for Class 11 related to trigonometric functions below.
- If in a circle of radius r, an arc of length l subtends an angle of θ radians, then l = r×θ.
- Trigonometric ratios:
- sin θ = (Perpendicular (P)) / (Hypotenuse (H)).
- cos θ = (Base (B)) / ( Hypotenuse (H)).
- tan θ = (Perpendicular (P)) / (Base (B)).
- cosec θ = (Hypotenuse (H)) / (Perpendicular (P)).
- sec θ = (Hypotenuse (H)) / (Base (B)).
- cot θ = (Base (B)) / (Perpendicular (P)).
- Reciprocal Trigonometric Ratios:
- sin θ = 1 / (cosec θ)
- cosec θ = 1 / (sin θ)
- cos θ = 1 / (sec θ)
- sec θ = 1 / (cos θ)
- tan θ = 1 / (cot θ)
- cot θ = 1 / (tan θ)
- Trigonometric Ratios of Complementary Angles:
- sin (90° – θ) = cos θ
- cos (90° – θ) = sin θ
- tan (90° – θ) = cot θ
- cot (90° – θ) = tan θ
- sec (90° – θ) = cosec θ
- cosec (90° – θ) = sec θ
- Periodic Trigonometric Ratios
- sin(π/2-θ) = cos θ
- cos(π/2-θ) = sin θ
- sin(π-θ) = sin θ
- cos(π-θ) = -cos θ
- sin(π+θ)=-sin θ
- cos(π+θ)=-cos θ
- sin(2π-θ) = -sin θ
- cos(2π-θ) = cos θ
- Trigonometric Identities
- sin2 θ + cos2 θ = 1 ⇒ sin2 θ = 1 – cos2 θ ⇒ cos2 θ = 1 – sin2 θ
- cosec2 θ – cot2 θ = 1 ⇒ cosec2 θ = 1 + cot2 θ ⇒ cot2 θ = cosec2 θ – 1
- sec2 θ – tan2 θ = 1 ⇒ sec2 θ = 1 + tan2 θ ⇒ tan2 θ = sec2 θ – 1
- Product to Sum Formulas
- sin x sin y = 1/2 [cos(x–y) − cos(x+y)]
- cos x cos y = 1/2[cos(x–y) + cos(x+y)]
- sin x cos y = 1/2[sin(x+y) + sin(x−y)]
- cos x sin y = 1/2[sin(x+y) – sin(x−y)]
- Sum to Product Formulas
- sin x + sin y = 2 sin [(x+y)/2] cos [(x-y)/2]
- sin x – sin y = 2 cos [(x+y)/2] sin [(x-y)/2]
- cos x + cos y = 2 cos [(x+y)/2] cos [(x-y)/2]
- cos x – cos y = -2 sin [(x+y)/2] sin [(x-y)/2]
- General Trigonometric Formulas:
- sin (x+y) = sin x × cos y + cos x × sin y
- cos(x+y)=cosx×cosy−sinx×siny
- cos(x–y)=cosx×cosy+sinx×siny
sin(x–y)=sinx×cosy−cosx×siny - If there are no angles x, y and (x ± y) is an odd multiple of (π / 2); then:
- tan (x+y) = tan x + tan y / 1 − tan x tan y
- tan (x−y) = tan x − tan y / 1 + tan x tan y
- If there are no angles x, y and (x ± y) is an odd multiple of π; then:
- cot (x+y) = cot x cot y−1 / cot y + cot x
- cot (x−y) = cot x cot y+1 / cot y − cot x
- Formulas for twice of the angles:
- sin2θ = 2sinθ cosθ = [2tan θ /(1+tan2θ)]
- cos2θ = cos2θ–sin2θ = 1–2sin2θ = 2cos2θ–1= [(1-tan2θ)/(1+tan2θ)]
- tan 2θ = (2 tan θ)/(1-tan2θ)
- Formulas for thrice of the angles:
- sin 3θ = 3sin θ – 4sin 3θ
- cos 3θ = 4cos 3θ – 3cos θ
- tan 3θ = [3tan θ–tan 3θ]/[1−3tan 2θ]
Chapter 4: Principle of Mathematical Induction
As the name suggests, the chapter explains the concept of the Principle of Mathematical Induction. The topics discussed are the process to prove the induction and motivating the application taking natural numbers as the least inductive subset of real numbers. One key basis for mathematical thinking is deductive reasoning. In contrast to deduction, inductive reasoning depends on working with different cases and developing a conjecture by observing incidences till we have observed each and every case. Thus, in simple language we can say the word ‘induction’ means the generalisation from particular cases or facts.
Below mentioned is the list of some important terms and steps used in the chapter mentioned above:
- Statement: A sentence is called a statement if it is either true or false.
- Motivation: Motivation is tending to initiate an action. Here Basis step motivate us for mathematical induction.
- Principle of Mathematical Induction: The principle of mathematical induction is one such tool that can be used to prove a wide variety of mathematical statements. Each such statement is assumed as P(n) associated with positive integer n, for which the correctness for the case n = 1 is examined. Then assuming the truth of P(k) for some positive integer k, the truth of P (k+1) is established.
- Working Rule:
- Step 1: Show that the given statement is true for n = 1.
- Step 2: Assume that the statement is true for n = k.
- Step 3: Using the assumption made in step 2, show that the statement is true for n = k + 1. We have proved the statement is true for n = k. According to step 3, it is also true for k + 1 (i.e., 1 + 1 = 2). By repeating the above logic, it is true for every natural number.
Chapter 5: Complex Numbers and Quadratic Equations
As the name of the chapter suggests, therefore, this chapter explains the concept of complex numbers and quadratic equations and their properties. The topics discussed are the square root, algebraic properties, argand plane and polar representation of complex numbers, solutions of quadratic equations in the complex number system. A few important points related to the Complex Numbers and Quadratic Equations are as follows:
- Complex Numbers: A number that can be expressed in the form a + b is known as the complex number; where a and b are the real numbers and i is the imaginary part of the complex number.
- Imaginary Numbers: The square root of a negative real number is called an imaginary number, e.g. √-2, √-5 etc. The quantity √-1 is an imaginary unit and it is denoted by ‘i’ called iota.
i = √-1, i2 = -1, i3 = -i, i4 = 1
- Equality of Complex Number: Two complex numbers z1 = x1 + iy1 and z2 = x2 + iy2 are equal, if x1 = x2 and y1 = y2 i.e. Re(z1) = Re(z2) and Im(z1) = Im(z2)
Algebra of Complex Numbers
- Addition: Consider z1 = x1 + iy1 and z2 = x2 + iy2 are any two complex numbers, then their sum is defined as
z1 + z2 = (x1 + iy1) + (x2 + iy2) = (x1 + x2) + i (y1 + y2)
- Subtraction: Consider z1 = (x1 + iy1) and z2 = (x2 + iy2) are any two complex numbers, then their difference is defined as
z1 – z2 = (x1 + iy1) – (x2 + iy2) = (x1 – x2) + i(y1 – y2)
- Multiplication: Consider z1 = (x1 + iy1) and z2 = (x2 + iy2) be any two complex numbers, then their multiplication is defined as
z1z2 = (x1 + iy1) (x2 + iy2) = (x1x2 – y1y2) + i (x1y2 + x2y1)
- Division: Consider z1 = x1 + iy1 and z2 = x2 + iy2 be any two complex numbers, then their division is defined as
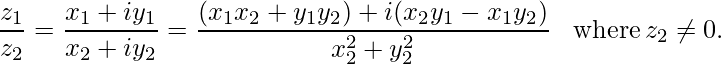
Conjugate of Complex Number
Consider z = x + iy, if ‘i’ is replaced by (-i), then it is called to be conjugate of the complex number z and it is denoted by z¯, i.e.
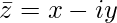
Modulus of a Complex Number
Consider z = x + y be a complex number. So, the positive square root of the sum of square of real part and square of imaginary part is called modulus (absolute values) of z and it is denoted by |z| i.e.
|z| = √x2+y2
Argand Plane
Any complex number z = x + y can be represented geometrically by a point (x, y) in a plane, called argand plane or gaussian plane.
- A pure number x, i.e. (x + 0i) is represented by the point (x, 0) on X-axis. Therefore, X-axis is called real axis.
- A purely imaginary number y i.e. (0 + y) is represented by the point (0, y) on the y-axis. Therefore, the y-axis is called the imaginary axis.
Argument of a complex Number
The angle made by line joining point z to the origin, with the positive direction of X-axis in an anti-clockwise sense is called argument or amplitude of complex number. It is denoted by the symbol arg(z) or amp(z).
arg(z) = θ = tan-1(y/x)
- Principal Value of Argument
- When x > 0 and y > 0 ⇒ arg(z) = θ
- When x < 0 and y > 0 ⇒ arg(z) = π – θ
- When x < 0 and y < 0 ⇒ arg(z) = -(π – θ)
- When x > 0 and y < 0 ⇒ arg(z) = -θ
Polar Form of a Complex Number
When z = x + iy is a complex number, so z can be written as,
- z = |z| (cosθ + isinθ), where θ = arg(z).
which is known as the polar form. Now, when the general value of the argument is θ, so the polar form of z is written as,
- z = |z| [cos (2nπ + θ) + isin(2nπ + θ)], where n is an integer.
Chapter 6: Linear Inequalities
The chapter explains the concept of Linear Inequalities. The topics discussed are algebraic solutions and graphical representation of Linear Inequalities in one variable and two variables respectively. In mathematics, an inequality is a relation that holds between two values when they are different, Solving linear inequalities is very similar to solving linear equations, except for one small but important detail: you flip the inequality sign whenever you multiply or divide the inequality by a negative.
Inequation: An inequation or inequality is a statement involving variables and the sign of inequality like >, <, ≥ or ≤.
- Symbols used in inequalities
- The symbol < means less than.
- The symbol > means greater than.
- The symbol < with a bar underneath ≤ means less than or equal to.
- The symbol > with a bar underneath ≥ means greater than or equal to.
- The symbol ≠ means the quantities on the left and right sides are not equal to.
Algebraic Solutions for Linear Inequalities in One Variable and its Graphical Representation
Using the trial-and-error method, the solution to the linear inequality can be determined. However, this method isn’t always possible, and computing the solution takes longer. So, using a numerical approach, the linear inequality can be solved. When solving linear inequalities, remember to follow these rules:
Rule 1: Don’t change the sign of an inequality by adding or subtracting the same integer on both sides of an equation.
Rule 2: Add or subtract the same positive integer from both sides of an inequality equation.
Chapter 7: Permutations and Combinations
The present chapter explains the concepts of permutation (an arrangement of a number of objects in a definite order) and combination (a collection of the objects irrespective of the order). The topics discussed are the fundamental principle of counting, factorial, permutations, combinations, and their applications along with the concept of restricted permutation. If a certain event occurs in ‘m’ different ways followed by an event that occurs in ‘n’ different ways, then the total number of occurrences of the events can be given in m × n order. Find the important Maths formulas for class 11 Permutations and Combinations are as under:
- Factorial: The continued product of first n natural number is called factorial ‘n’. It is denoted by n! which is given by,
n! = n(n – 1)(n – 2)… 3 × 2 × 1 and 0! = 1! = 1
- Permutations: Permutation refers to the various arrangements that can be constructed by taking some or all of a set of things. The number of an arrangement of n objects taken r at a time, where 0 < r ≤ n, denoted by nPr is given by
nPr = n! / (n−r)!
- The number of permutation of n objects of which p1 are of one kind, p2 are of second kind,… pk are of kth kind such that p1 + p2 + p3 + … + pk = n is
n! / p1! p2! p3! ….. pk!
- Combinations: Combinations are any of the various selections formed by taking some or all of a number of objects, regardless of their arrangement. The number of r objects chosen from a set of n objects is indicated by nCr, and it is given by
nCr = n! / r!(n−r)!
- Relation Between Permutation and combination: The relationship between the two concepts is given by two theorems as,
- nPr = nCr r! when 0 < r ≤ n.
- nCr + nCr-1 = n+1Cr
Chapter 8: Binomial Theorem
This chapter discusses the binomial theorem for positive integers used to solve complex calculations. The topics discussed are the history, statement, and proof of the binomial theorem and its expansion along with Pascal’s triangle. A Binomial Theorem helps to expand a binomial given for any positive integer n.
- Binomial Theorem: The expansion of a binomial for any positive integer n is given by Binomial Theorem, which is
(a + b)n = nC0 an + nC1 an-1 b + nC2 an-2 b2 + … + nCn-1 a bn-1 + nCn bn
- Some special cases from the binomial theorem can be written as:
- (x – y)n = nC0 xn – nC1 xn-1 y + nC2 xn-2 y2 + … + (-1)n nCn xn
- (1 – x)n = nC0 – nC1 x + nC2 x2 – …. (-1)n nCn xn
- nC0 = nCn = 1
- Pascal’s triangle: The coefficients of the expansions are arranged in an array called Pascal’s triangle.
- General Term of following expansions are:
- (a + b)n is Tr+1 = nCr an−r.br
- (a – b)n is (-1)r nCr an−r.br
- (1 + x)n = nCr . xr
- (1 – x)n = (-1)r nCn xr
- Middle Terms: In the expansion (a + b)n, if n is even, then the middle term is the (n/2 + 1)th term. If n is odd, then the middle terms are (n/2 + 1)th and ((n+1)/2+1)th terms.
Chapter 9: Sequences and Series
The chapter Sequences and Series discuss the concepts of a sequence (an ordered list of numbers) and series (the sum of all the terms of a sequence). The topics discussed are sequence and series, arithmetic and geometric progression, arithmetic, and geometric mean. Here is the list of some important terms used in Sequence and Series are as listed below:
- Progression: A sequence whose terms follow certain patterns is known as progression.
- Arithmetic Progression (AP): An arithmetic progression (A.P.) is a sequence where the terms either increase or decrease regularly by the same constant. This constant is called the common difference (d). The first term is denoted by a and the last term of an AP is denoted by l.
- For an Arithmetic Series: a, a+d, a+2d, a+3d, a+4d, …….a +(n-1)d
- The first term: a1 = a,
- The second term: a2 = a + d,
- The third term: a3 = a + 2d,
- The nth term: an = a + (n – 1)d
- nth term of an AP from the last term is a’n =an – (n – 1)d.
- an + a’n = constant
- Common difference of an AP i.e. d = an – an-1, ∀ n>1.
- Sum of n Terms of an AP: Sn = n/2 [2a + (n – 1)d] = n/2 (a1+ an)
- A sequence is an AP If the sum of n terms is of the form An2 + Bn, where A and B are constant and A = half of common difference i.e. 2A = d.
an =Sn – Sn-1
- Arithmetic Mean: If a, A and b are in A.P then A = (a+b)/2 is called the arithmetic mean of a and b. If a1, a2, a3,……an are n numbers, then their arithmetic mean is given by:
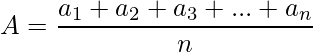
- The common difference is given as, d = (b – a)/(n + 1)
- The Sum of n arithmetic mean between a and b is, n (a+b/2).
- Geometric Progression (GP): A sequence in which the ratio of two consecutive terms is constant is called geometric progression.
- The constant ratio is called common ratio (r).
i.e. r = an+1/an, ∀ n>1 - The general term or nth term of GP is an =arn-1
- nth term of a GP from the end is a’n = 1/rn-1, l = last term
- If a, b and c are three consecutive terms of a GP then b2 = ac.
- Geometric Mean (GM): If a, G and b are in GR then G is called the geometric mean of a and b and is given by G = √(ab).
- If a,G1, G2, G3,….. Gn, b are in GP then G1, G2, G3,……Gn are in GM’s between a and b, then
common ratio is: 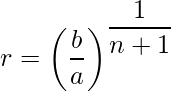
- If a1, a2, a3,…, an are n numbers are non-zero and non-negative, then their GM is given by
GM = (a1 . a2 . a3 …an)1/n - Product of n GM is G1 × G2 × G3 ×… × Gn = Gn = (ab)n/2
- Sum of first n natural numbers is: Σn = 1 + 2 + 3 +… + n = n(n+1)/2
- Sum of squares of first n natural numbers is: Σn2 = 12 + 22 + 32 + … + n2 = n(n+1)(2n+1)/6
- Sum of cubes of first n natural numbers is: Σn3 = 13 + 23 + 33 + .. + n3 = (n(n+1)(2n+1)/6)2
Chapter 10: Straight Lines
Straight lines defined the concept of the line, its angle, slope, and general equation. The topics discussed are the slope of a line, the angle between two lines, various forms of line equations, general equation of a line, and family of lines respectively. Here are some important formulas used in the Chapter Straight lines:
- Distance Formula: The distance between two points A(x1, y1) and B (x2, y2) is given by,
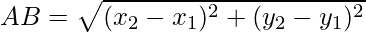
- The distance of a point A(x, y) from the origin 0 (0, 0) is given by OA = √(x2 + y2).
- Section Formula: The coordinates of the point which divides the joint of (x1, y1) and (x2, y2) in the ratio m:n internally, is
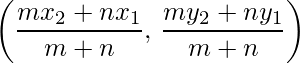
And externally is:
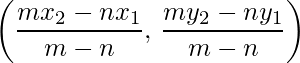
- Mid-Point of the joint of (x1, y1) and (x2, y2) is:
 .
.- X-axis divides the line segment joining (x1, y1) and (x2, y2) in the ratio -y1 : y2.
- Y-axis divides the line segment joining (x1, y1) and (x2, y2) in the ratio -x1 : x2.
- Coordinates of Centroid of a Triangle with vertices (x1, y1), (x2, y2) and (x3, y3) is
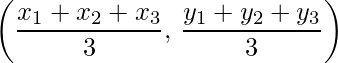
- Area of Triangle: The area of the triangle, the coordinates of whose vertices are (x1, y1), (x2, y2) and (x3, y3) is,
![Rendered by QuickLaTeX.com \begin{aligned}\text{Area of Triangle}&=\dfrac{1}{2}\begin{vmatrix}x_1&x_2&1\\x_2&y_2&1\\x_3&x_2&1\end{vmatrix}\\&=\dfrac{1}{2}\left[x_1(y_2-y_3)+x_2(y_3-y_1)+x_3(y_1-y_2)\right]\end{aligned}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-6a4aeb7acecdfe4c3fe0235a0b920c1f_l3.png)
- If the points (x1, y1), (x2, y2) and (x3, y3) are collinear, then x1 (y2 – y3) + x2 (y3 – y1) + x3 (y1 – y2) = 0.
- Slope or Gradient of Line: The inclination of angle θ to a line with a positive direction of X-axis in the anti-clockwise direction, the tangent of angle θ is said to be slope or gradient of the line and is denoted by m. i.e.
m = tan θ
- The slope of a line passing through points P(x1, y1) and Q(x2, y2) is given by,
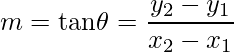
- Angle between Two Lines: The angle θ between two lines having slope m1 and m2 is,
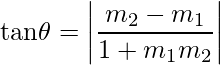
- If two lines are parallel, their slopes are equal i.e. m1 = m2.
- If two lines are perpendicular to each other, then their product of slopes is -1 i.e. m1m2 = -1.
- Point of intersection of two lines: Let equation of lines be ax1 + by1 + c1 = 0 and a2x + b2y + c2 = 0, then their point of intersection is
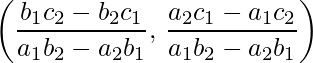
- Distance of a Point from a Line: The perpendicular distanced of a point P(x1, y1)from the line Ax + By + C = 0 is given by,
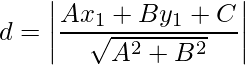
- Distance Between Two Parallel Lines: The distance d between two parallel lines y = mx + c1 and y = mx + c2 is given by,
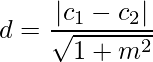
- Different forms of Equation of a line:
- If a line is at a distance k and parallel to X-axis, then the equation of the line is y = ± k.
- If a line is parallel to Y-axis at a distance of c from the Y-axis, then its equation is x = ± c.
- General Equation of a Line: Any equation of the form Ax + By + C = 0, where A and B are simultaneously not zero is called the general equation of a line
- Normal form: The equation of a straight line upon which the length of the perpendicular from the origin is p and angle made by this perpendicular to the x-axis is α, is given by: x cos α + y sin α = p.
- Intercept form: The equation of a line that cuts off intercepts a and b respectively on the x and y-axes is given by: x/a + y/b = 1.
- Slope-intercept form: The equation of the line with slope m and making an intercept c on the y-axis, is y = mx + c.
- One point-slope form: The equation of a line that passes through the point (x1, y1) and has the slope of m is given by y – y1 = m (x – x1).
- Two points form: The equation of a line passing through the points (x1, y1) and (x2, y2) is given by
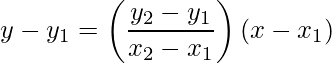
Chapter 11: Conic Sections
The topics discussed in the chapter Conic Sections are the sections of a cone, the degenerate case of a conic section along the equations and properties of conic sections. A circle is a geometrical figure where all the points in a plane are located equidistant from the fixed point on a given plane. Following are the list of some important formulas discussed in the chapter Conic Sections as,
- Equation of a circle with radius r having a centre (h, k) is given by (x – h)2 + (y – k)2 = r2.
- The general equation of the circle is given by x2 + y2 + 2gx + 2fy + c = 0 , where, g, f and c are constants.
- The centre of the circle is (-g, -f).
- The radius of the circle is r = √(g2 + f2 − c)
- The parametric equation of the circle x2 + y2 = r2 are given by x = r cos θ, y = r sin θ, where θ is the parameter.
- And the parametric equation of the circle (x – h)2 + (y – k)2 = r2 are given by x = h + r cos θ, y = k + r sin θ.
- Parabola: A parabola is the set of points P whose distances from a fixed point F in the plane are equal to their distance from a fixed-line l in the plane. The fixed point F is called focus and the fixed-line l is the directrix of the parabola.
Different forms of parabola
| y2= 4ax
| y2 = -4ax
| x2 = 4ay
| x2 = -4ay
|
Axis of parabola
| y = 0
| y = 0
| x = 0
| x = 0
|
Directrix of parabola
| x = -a
| x = a
| y = -a
| y = a
|
Vertex
| (0, 0)
| (0, 0)
| (0, 0)
| (0, 0)
|
Focus
| (a, 0)
| (-a, 0)
| (0, a)
| (0, -a)
|
Length of latus rectum
| 4a
| 4a
| 4a
| 4a
|
Focal length
| |x + a|
| |x – a|
| |y + a|
| |y – a|
|
- Ellipse: An ellipse is the set of all points in the plane whose distances from a fixed point in the plane bears a constant ratio, less than to their distance from a fixed point in the plane. The fixed point is called focus, the fixed line a directrix and the constant ratio (e) the eccentricity of the ellipse. The two standard forms of ellipse with their terminologies are mentioned below in the table:
Different forms of Ellipse
| x2/a2 + y2/b2= 1, a > b
| x2/b2 + y2/a2= 1, a > b
|
Equation of Major Axis
| y = 0
| x = 0
|
Length of Major Axis
| 2a
| 2a
|
Equation of Minor Axis
| x = 0
| y = 0
|
Length of Minor Axis
| 2b
| 2b
|
Equation of Directrix
| x = ±a/e
| y = ±a/e
|
Vertex
| (±a, 0)
| (0, ±a)
|
Focus
| (±ae, 0)
| (0, ±ae)
|
Length of latus rectum
| 2b2/a
| 2b2/a
|
- Hyperbola: A hyperbola is the locus of a point in a plane which moves in such a way that the ratio of its distance from a fixed point in the same plane to its distance from a fixed line is always constant which is always greater than unity. The fixed point is called the focus, the fixed line is called the directrix and the constant ratio, generally denoted bye, is known as the eccentricity of the hyperbola. The two standard forms of hyperbola with their terminologies are mentioned below in the table:
Different forms of Hyperbola
| x2/a2 – y2/b2= 1
| x2/a2 – y2/b2= 1
|
Coordinates of centre
| (0, 0)
| (0, 0)
|
Coordinates of vertices
| (±a, 0)
| (0, ±a)
|
Coordinates of foci
| (±ae, 0)
| (0, ±ae)
|
Length of Conjugate axis
| 2b
| 2b
|
Length of Transverse axis
| 2a
| 2a
|
Equation of Conjugate axis
| x = 0
| y = 0
|
Equation of Transverse axis
| y = 0
| x = 0
|
Equation of Directrix
| x = ±a/e
| y = ±a/e
|
Eccentricity (e)
| √(a2+b2)/a2
| √(a2+b2)/a2
|
Length of latus rectum
| 2b2/a
| 2b2/a
|
Chapter 12: Introduction to Three-dimensional Geometry
As the name suggests, the chapter explains the concepts of geometry in three-dimensional space. The topics discussed are the coordinate axes and planes respectively, points coordinate, distance and section for points. The three planes determined by the pair of axes are known as coordinate planes with XY, YZ and ZX planes. Find below the important Maths formulas for Class 11 Introduction to Three-dimensional Geometry as:
- Coordinate Axes: In three dimensions, the coordinate axes of a rectangular cartesian coordinate system are three mutually perpendicular lines. These axes are called the X, Y and Z axes.
- Coordinate Planes: The three planes determined by the pair of axes are the coordinate planes. These planes are called XY, YZ and ZX planes and they divide the space into eight regions known as octants.
- Coordinates of a Point in Space: The coordinates of a point in the space are the perpendicular distances from P on three mutually perpendicular coordinate planes YZ, ZX, and XY respectively. The coordinates of a point P are written in the form of triplet like (x, y, z). The coordinates of any point on:
- X-axis is of the form (x, 0,0)
- Y-axis is of the form (0, y, 0)
- Z-axis is of the form (0, 0, z)
- XY-plane are of the form (x, y, 0)
- YZ-plane is of the form (0, y, z)
- ZX-plane are of the form (x, 0, z)
- Distance Formula: The distance between two points A(x1, y1, z1) and B(x2, y2, z2) is given by,
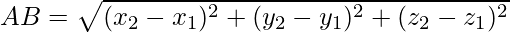
- While, the distance between two points A(x, y, z) from the origin O(0, 0, 0) is given by,
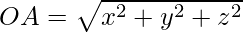
- Section Formula: The coordinates of the point R which divides the line segment joining two points P(x1, y1, z1) and Q(x2, y2, z2) internally or externally in the ratio m : n are given by,
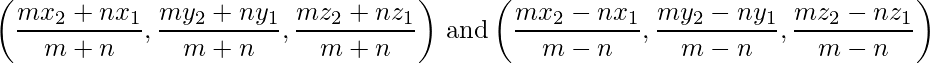
- Mid-Point of the joint of (x1, y1) and (x2, y2) is:

- Coordinates of Centroid of a Triangle with vertices (x1, y1), (x2, y2) and (x3, y3) is
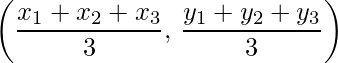
Chapter 13: Limits and Derivatives
The chapter explains the concept of calculus that deals with the study of change in the value of a function when the change occurs in the domain points. The topics discussed are the definition and algebraic operations of limits and derivatives respectively.
A limit of a function at a certain point holds a common value of the left as well as the right-hand limits if they coincide with each other. Here are the list of some important formulas used to solve problems on Limits and Derivatives as,
- Limit: Let y = f(x) be a function of x. If at x = a, f(x) takes indeterminate form, then we consider the values of the function which is very near to a. If these value tend to a definite unique number as x tends to a, then the unique number so obtained is called the limit of f(x) at x = a and we write it as
 .
. - Left Hand and Right-Hand Limits: If values of the function at the point which are very near to a on the left tends to a definite unique number as x tends to a, then the unique number so obtained is called the left-hand limit of f(x) at x = a, we write it as
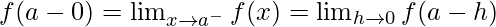
- Similarly, right hand limit is given as,
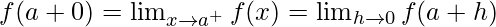
- A limit
 exists when:
exists when:
 and
and  both exists or,
both exists or,
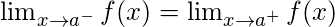
![Rendered by QuickLaTeX.com \begin{aligned}\lim_{x\to a}[f(x)\pm g(x)]&=\lim_{x\to a}f(x)\pm \lim_{x\to a} g(x)\\\lim_{x\to a}kf(x)&=k\lim_{x\to a}f(x)\\\lim_{x\to a}f(x)\cdot g(x)&=\lim_{x\to a}f(x)\times\lim_{x\to a}g(x)\\\lim_{x\to a}\dfrac{f(x)}{g(x)}&=\dfrac{\lim_{x\to a}f(x)}{\lim_{x\to a}g(x)}\end{aligned}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-f79d4730e45e635c86c80ba858728930_l3.png)

- Derivatives: Consider a real-valued function f, such that:

is known as the Derivative of function f at x if and only if,
 exists finitely.
exists finitely.
- Some Important Properties of Derivatives: Consider f and g be two functions such that their derivatives can be defined in a common domain as:
![Rendered by QuickLaTeX.com \begin{aligned}\dfrac{\mathrm{d}}{\mathrm{d}x}[f(x)+g(x)]&=\dfrac{\mathrm{d}}{\mathrm{d}x}[f(x)]+\dfrac{\mathrm{d}}{\mathrm{d}x}[g(x)]\\\dfrac{\mathrm{d}}{\mathrm{d}x}[f(x)-g(x)]&=\dfrac{\mathrm{d}}{\mathrm{d}x}[f(x)]-\dfrac{\mathrm{d}}{\mathrm{d}x}[g(x)]\\\dfrac{\mathrm{d}}{\mathrm{d}x}[f(x)\cdot g(x)]&=\left[\dfrac{\mathrm{d}}{\mathrm{d}x}f(x)\right]\cdot g(x)+f(x)\cdot\left[\dfrac{\mathrm{d}}{\mathrm{d}x}g(x)\right]\\\dfrac{\mathrm{d}}{\mathrm{d}x}\left[\dfrac{f(x)}{g(x)}\right]&=\dfrac{\left[\dfrac{\mathrm{d}}{\mathrm{d}x}f(x)\right]\cdot g(x)-f(x)\cdot \left[\dfrac{\mathrm{d}}{\mathrm{d}x}g(x)\right]}{[g(x)]^2}\end{aligned}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-deffb33d9df811e455f522770076822d_l3.png)
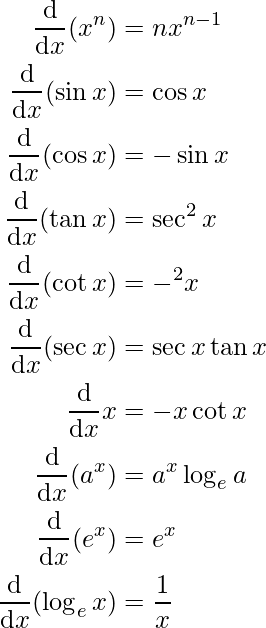
Chapter 14: Mathematical Reasoning
As the name suggests, the chapter explains the concepts of mathematical reasoning (a critical skill to analyze any given hypothesis in the context of mathematics). The topics discussed are statements, inductive reasoning, and deductive reasoning. Following are the list of important terms discussed as:
- Statements: A statement is a sentence which either true or false, but not both simultaneously. For example: “A triangle has four sides.”, “New Delhi is the capital of India.” are the statements.
- Negation of a statement: Negation of a statement p: If p denote a statement, then the negation of p is denoted by ∼p.
- Compound statement: A statement is a compound statement if it is made up of two or more smaller statements. The smaller statements are called component statements of the compound statement. The Compound statements are made by:
- Connectives: “AND”, “OR”
- Quantifiers: “there exists”, “For every”
- Implications: The meaning of implications “If ”, “only if ”, “ if and only if ”.
- “p ⇒ q” :
- p is a sufficient condition for q or p implies q.
- q is necessary to condition for p. The converse of a statement p ⇒ q is the statement q ⇒ p.
- p⇒ q together with its converse gives p if and only if q.
- “p ⇔ q”:
- p implies q (denoted by p ⇒ q)
- p is a sufficient condition for q
- q is a necessary condition for p
- p only if q
- ∼q implies ∼p
- Contrapositive: The contrapositive of a statement p ⇒ q is the statement ∼ q ⇒∼p.
- Contradiction: If to check whether p is true we assume negation p is true.
- Validating statements: Checking of a statement whether it is true or false. The validity of a statement depends upon which of the special. The following methods are used to check the validity of statements:
- direct method
- contrapositive method
- method of contradiction
- using a counterexample.
Chapter 15: Statistics
This chapter explains the concepts of statistics (data collected for specific purposes), dispersion, and methods of calculation for ungrouped and grouped data. The topics discussed are range, mean deviation, variance and standard deviation, and analysis of frequency distributions. Here one will find the essential maths formulas for Class 11 of Statistics given below:
- Measure of Dispersion: The dispersion is the measure of variations in the values of the variable. It measures the degree of scatteredness of the observation in a distribution around the central value.
- Range: The measure of dispersion which is easiest to understand and easiest to calculate is the range. Range is defined as the difference between two extreme observation of the distribution.
Range of distribution = Largest observation – Smallest observation.
Mean deviation for ungrouped data- For n observations x1, x2, x3,…, xn, the mean deviation about their mean x¯ is given by:
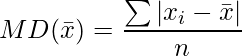
And, the Mean deviation about its median M is given by,

Mean deviation for discrete frequency distribution-
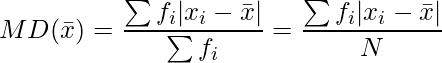
Variance: Variance is the arithmetic mean of the square of the deviation about mean x¯.
Let x1, x2, ……xn be n observations with x¯ as the mean, then the variance denoted by σ2, is given by
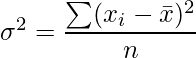
Standard deviation: If σ2 is the variance, then σ is called the standard deviation is given by
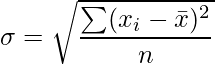
Standard deviation of a discrete frequency distribution is given by
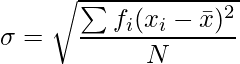
Coefficient of variation: In order to compare two or more frequency distributions, we compare their coefficient of variations. The coefficient of variation is defined as
Coefficient of variation = (Standard deviation / Mean) × 100
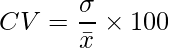
Chapter 16: Probability
Probability is a fundamental part of the Class 11 Maths curriculum and is important for Class 11 exams and different competitive exams like JEE and NEET. In previous classes, students may have learned the basic concept of probability as a measure of uncertainty of various phenomena. Here, a list of formulas, important properties, applications and a summary of the chapter is discussed, which will help students learn the related concepts quickly and score good marks in the exam.
The chapter discusses the concept of probability (a measure of uncertainty of various phenomena or a chance of occurrence of an event). The topics discussed are the random experiments, outcomes, sample spaces, event, and their type. Following is the list of important formulas and chapter summary for Class 11 Probability as:
- Probability = Number of Favourable outcomes in an Event / Total number of Outcomes
- Event: An event is a subset of the S (sample space). An empty set is also known as the Impossible event.
- For any random experiment, let S be the sample space. The probability P is a real-valued function whose domain is the power set of S and [0, 1] is the range interval. For any event E: P(E) ≥ 0 and P(S) = 1
- Mutually exclusive events: If E and F are mutually exclusive events, then: P(E ∪ F) = P(E) + P(F)
- Equally likely outcomes: All outcomes with equal probability are called equally likely outcomes. Let S be a finite sample space with equally likely outcomes and A be the event. Therefore, the probability of an event A is: P(A) = n(A) / n(S), where n(A) is the number of elements on the set A and n(S) is the Total number of outcomes or the number of elements in the sample space S
- Let P and Q be any two events, then the following formulas can be derived.
- Event P or Q: The set P ∪ Q
- Event P and Q: The set P ∩ Q
- Event P and not Q: The set P – Q
- P and Q are mutually exclusive if P ∩ Q = φ
- Events P1, P2, . . . . . , Pn are exhaustive and mutually exclusive if P1 ∪ P2 ∪ . . . . . ∪ Pn = S and Ei ∩ Ej = φ for all i ≠ j.
Share your thoughts in the comments
Please Login to comment...