Trigonometry Formulas Class 10

Trigonometry Formula in Class 10 is the list of all formulas used in Trigonometry useful for class 10 students in their exams. Trigonometry is the branch of mathematics that establishes the relation of the angle of a right triangle with the ratio of sides. Trigono means triangle and metron means measure. There are in total six trigonometric ratios namely, sine, cosine, tangent, cotangent, secant, and cosecant. The Trigonometric Formulas establish relations between these Trigonometric Ratios.

In this article, we will learn Trigonometric Formulas essential for Class 10 along with the Trigonometric Ratio Table.

What is Trigonometry Ratio?

Trigonometric Ratios are the ratio of sides of a right triangle for a given value of the angle denoted as theta(θ). There are six trigonometric ratios namely, sine, cosine, tangent, cotangent, secant, and cosecant. The angle θ is defined as the angle between the base and the hypotenuse of the right triangle.

Trigonometric Ratio Formulas Class 10

Trigonometric Ratio Formulas establish the relation between Trigonometric Ratios and the sides of a right triangle. The T-Ratios Formulas Class 10 are listed below:

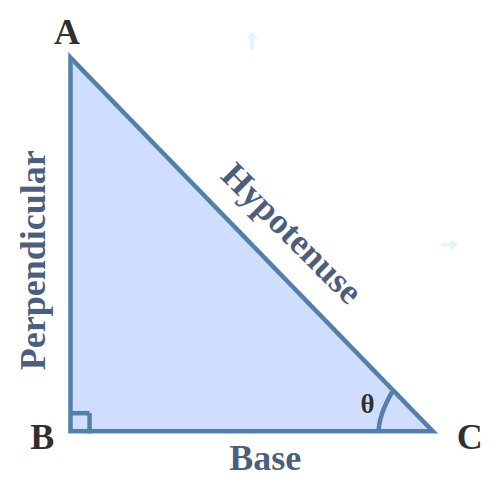
• sin θ = Perpendicular/Hypotenuse
• cos θ = Base/Hypotenuse
• tan θ = Perpendicular/Base
• cosec θ = Hypotenuse/Perpendicular
• sec θ = Hypotenuse/Base
• cot θ = Base/Perpendicular

Trigonometric Ratio Table Class 10

Trigonometric Ratio Table contains the value of all the six trigonometric ratios at some standard angles 0°, 30°, 45°, 60° and 90°.

θ	0°	30°	45°	60°	90°
sin θ	0	1/2	1/√2	√3/2	1
cos θ	1	√3/2	1/√2	1/2	0
tan θ	0	1/√3	1	√3	Not defined
cosec θ	Not defined	2	√2	2/√3	1
sec θ	1	2/√3	√2	2	Not defined
cot θ	Not defined	√3	1	1/√3	0

All Trigonometry Formulas Class 10

List of all Trigonometric Formulas essential for Class 10 is mentioned below:

Trigonometric Reciprocal Identities

• sin θ = 1/cosec θ ⇒ cosec θ = 1/sin θ
• cos θ = 1/sec θ ⇒ sec θ = 1/cos θ
• tan θ = 1/cot θ ⇒ cot θ = 1/tan θ

Trigonometric Identities

• sin²θ + cos²θ = 1
• 1 + tan²θ = sec²θ
• 1 + cot²θ = cosec²θ

Complementary Angle Formulas

• sin(90 – θ) = cos θ
• cos(90 – θ) = sin θ
• tan(90 – θ) = cot θ
• cot(90 – θ) = tan θ
• sec(90 – θ) = cosec θ
• cosec(90 – θ) = sec θ

Supplementary Angle Formulas

• sin(180 – θ) = sin θ
• cos(180 – θ) = -cos θ
• tan(180 – θ) = -tan θ
• cot(180 – θ) = -cot θ
• sec(180 – θ) = -secθ
• cosec(180 – θ) = cosec θ

Even and Odd Angle Formulas

• sin(-θ) = -sin θ
• cos(-θ) = cos θ
• tan(-θ) = -tan θ
• cot(-θ) = -cot θ
• sec(-θ) = sec θ
• cosec(-θ) = -cosec θ

Double Angle Formulas

• sin 2θ = 2sinθ.cosθ
• cos 2θ = 1 – 2sin²θ
• tan 2θ = 2tanθ/(1-tan²θ)

Solved Examples on Trigonometry Formulas Class 10

Example 1: If sin A = 3/4. Calculate cos A and tan A

Solution:

cos²A = 1 – sin²A

⇒ cos²A = 1-(9/16)

⇒ cos²A = 7/16

⇒ cosA = √7/4

⇒ tanA = sinA/cosA

⇒ tanA = 3/√7

Example 2: Given 15 cot A = 8. Find sin A and sec A

Solution:

cotA = 8/15

⇒ cosec²A = 1 + cot²A

⇒ cosec²A = 1 + (64/225)

⇒ cosec²A = 289/225

⇒ cosecA = 17/15

⇒ sinA = 15/17

⇒ secA = cosecA/cotA

⇒ secA = 17/8

Example 3: Find the value of sin 45° – cos 45°.

Solution:

sin 45° = cos 45° = 1/√(2)

⇒ sin 45° – cos 45° = 0

Example 4: If tan θ + cot θ = 7. Find tan²θ + cot²θ

Solution:

tan θ + cot θ = 7

⇒ (tanθ + cotθ)² = 49

⇒ tan²θ + cot²θ + 2tanθcotθ = 49

⇒ tan²θ + cot²θ + 2 = 49

⇒ tan²θ + cot²θ = 47

Example 5: The value of tan θ = 3/4. Find the value of sec θ.

Solution:

1 + tan²θ = sec²θ

⇒ 1 +(3/4)² = sec²θ

⇒ sec²θ = 25/16

⇒ secθ = 5/4

Example 6: If sec θ + tan θ = 5. Find sec θ – tan θ.

Solution:

sec 2θ – tan 2θ = 1

⇒ (sec θ + tan θ)(sec θ – tan θ) = 1

⇒ 5(sec θ – tan θ) = 1

⇒ sec θ – tan θ = 1/5

Practice Questions on Trigonometric Formulas Class 10

1. Prove that (cos θ/(1 – tan θ)) + (sin θ/(1 – cot θ)) = sin θ + cos θ.

2. Prove that tan²θ + cot²θ +2 = sec²θ * cosec²θ.

3. If cosec θ + cot θ = 9. find cos θ.

4. If cos θ = 4/5. Find all other trigonometric ratios.

5. Find the value of sin 60° cos 30° + cos 30° sin 60°.

6. Find the value of tan 30°/cot 60°.

7. Find the value of (sin 30° + cos 30°) – (sin 60° + cos 60°).

8. If tanθ + cotθ = 1. Find the value of tan¹⁰θ + cot¹⁰θ.

9. Find the value of sin 45° + cos 45°.

10. Find the value of cos 19°/sin 71°.

Trigonometry Formula Class 10 – FAQs

1. What are Trigonometric Ratio Formulas in Class 10.

Trigonometric Ratio Formulas establish the relation between Trigonometric Ratios and the sides of a right triangle.

2. What is Reciprocal of tan θ?

cotθ = 1/tanθ

3. What is the value of sin(-θ)?

sin(-θ) = -sinθ

4. What is the relation between cot θ and cosec θ?

1 + cot²θ = cosec²θ

5. How is tan θ related to sin θ and cos θ?

tan θ = sin θ/cos θ

6. What is the value of sin 30?

sin 30 = 1/2

7. How is cosecθ related to sinθ?

cosecθ = 1/sinθ

8. What is the value of tan 45?

tan 45 = 1

9. What is the value of Cos(-θ)?

cos(-θ) = cosθ

10. Is Trigonoimetry Formula Class 10 important?

Yes, Trigonometry Formula Class 10 is very important for Class 10 students as they can always expect questions from this in their exams.