What are Coordinate Geometry Formulas?
Last Updated :
10 Dec, 2021
Geometry is a study of mathematics that includes points, lines, angles, curves, shapes, properties, and parameters. The shapes are either plotted on plane surfaces or real environment. 2D shapes are flat shapes like squares, circles, triangles which are presented on plane surfaces. Whereas, 3D shapes have three dimensions length, breadth, and width which are found around us.
Coordinate geometry
Coordinate geometry or also known as Cartesian geometry is a study of geometry related to using the coordinate points to plot different geometrical shapes like line, curve, triangle, parabola, hyperbola, etc. The points are plotted on a plane using an ordered pair of numbers.
Coordinate geometry is used to calculate the distance between two points, divide the lines in the ratio of m:n, and find the midpoint of a line in geometry.
What is the coordinate geometry formula?
Answer:
The formulas of coordinate geometry define various properties of points, lines, and figures represented on the plane with reference to the X-axis and Y-axis. Below these formulas have been discussed with a proper explanation along with their mathematical representation,
For the distance formula between two points, let us suppose two points be A and B with coordinates (x,y) and (x,y) will be equal to the square root of the sum of the square of the difference of x coordinates and y coordinate. Mathematically,
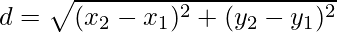
A slope can be defined as the inclination of a surface or a line. For the calculation of slope, the angle needs to be known made by the lines with the positive axis, or take any two points on the line as reference. Let a slope be inclined at an angle θ with a positive X-axis, so that
Slope(m) = Tanθ
Or, let (x1, y1) and (x2,y2) be the two points on the line, then
Slope(m) = y2 – y1/x2 – x1
The midpoint lies exactly between the two points. to find the midpoint of a line connecting two points let us take two points A and B with coordinates (x,y) and (x,y). And, let M(x,y) be the midpoint located on the line. The midpoint formula for the given point A and B will be given by,
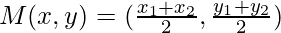
Section formula is used to divide a line in the ratio m:n having points (x, y) and (x, y). The dividing point lies between the two joining points in the line. The section formula for the line having joining points (x, y) and (x, y) be given by,
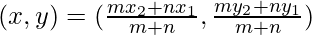
the area of a triangle in a coordinate geometry is determined when all three vertices are known. Let (x, y), (x, y) and (x, y) be the three vertices of a triangle. Then, its area can be computed by,
![Rendered by QuickLaTeX.com Area=\frac{1}{2}[x_1(y_2-y_3)+x_2(y_3-y_1)+x_3(y_1-y_2)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e807b8c1a11658464c4d31f4f387245e_l3.png)
Sample Problems
Question 1: Find the distance between two points A(2, 3) and B(4, 1).
Solution:
A(2, 3) = A(x1, y1)
B(4, 1) = B(x2, y2)
Using the distance formula,
d = 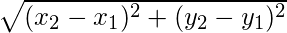
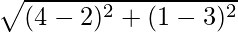
√(4+4)
√8
2√2 units
Question 2: Find the slope of the line if the two points on the line are P(0, -1) and Q(4, 1).
Solution:
P(0, -1) = P(x1, y1)
Q(4, 1) = Q(x2, y2)
Using the slope formula
m = y2 – y1/x2 – x1
m = 1 – (-1)/4 – 0
m = 2/4
m = 1/2
Question 3: Find the midpoint of the line having joining points (-8, -9) and (0, -3).
Solution:
A(-8, -9) = A(x1, y1)
B(0, -3) = B(x2, y2)
Using the mid point formula,
Mid point (x, y) = (-8 + 0/2 , -9 + (-3)/2)
(x, y) = (-4, -6)
Question 4: Find the area of the triangle having its vertices P(2, 3), Q(6, 3), and R(2, 6).
Solution:
P(2, 3) = P(x1, y1)
Q(6, 3) = Q(x2, y2)
R(2, 6) = R(x3, y3)
By the area formula,
Area = ![Rendered by QuickLaTeX.com \frac{1}{2}[x_1(y_2-y_3)+x_2(y_3-y_1)+x_3(y_1-y_2)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-0e197b6bfdb755fa045771320c49473d_l3.png)
1/2[2(3 – 6) + 6(6 – 3) + 2(2 – 2)]
1/2[2 × (-3) + 6 × 3 + 2 × 0]
1/2[-6 + 18]
1/2 × 12
6 units
Share your thoughts in the comments
Please Login to comment...