Conic sections are used in everyday life, from a guitar, flyover to a football. Everything has a curve that belongs to the curves of conic sections. There are four types of conic sections – circles, parabola, ellipse, and hyperbola. Hyperbola and Ellipse are similar kinds of conic sections. A hyperbola is defined as a curve that is made of all the sets of points the difference of whose distances from the two fixed points in the plane is constant. Some examples of hyperbola are the boundary of a guitar. Let’s look at the curve in more detail.
What is Hyperbola?
A hyperbola is defined as the set of points in a plane, the difference of whose distances from two fixed points in the plane is constant. The figure below shows the basic shape of the hyperbola with its different parts. We have four points P1, P2, P3, and P4. We measure the difference between the distances of each point from F1 and F2.

The difference in the distance that we talk about while defining the hyperbola is the difference between the distance from the farther point and the nearer point. These two points are called foci of the hyperbola. The mid-point of the line segment joining them is called the center of the hyperbola. In the given figure, the line that passes through the two foci is called the transverse axis of the hyperbola and the line that is drawn perpendicular to the traverse axis is called the conjugate axis. Vertices of the parabola are defined as the points where the curve intersects the traverse axis.

Let’s say the distance between the two foci is given by “2c”, the distance between two vertices can be said “2a”. Let’s define b,
b = 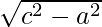
The length of the conjugate axis is 2b.
Now let’s calculate the difference between P1F1 and P1F2. Consider the above figure, we have taken to points A and B at the vertices. We know,
BF1 – BF2 = AF2 – AF1
BA + AF1 – BF2 = AB + BF2 – AF1
AF1 = BF2
So that, BF1 – BF2 = BA + AF1 – BF2 = BA = 2a
Eccentricity
The eccentricity is defined as the ratio of “c” and “a”. We know that c ≥ a, that’s why its value lies between and 0 and 1.
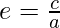
Distance between foci in terms of eccentricity is given by 2ae.
Standard Equations of Hyperbola
There are two types of standard equations of hyperbola which are possible. In standard equations, usually, we assume that the center of the hyperbola is at the origin and the foci are on the x and y axes respectively. The figure below shows two possibilities in the standard equation of a hyperbola.

Let’s derive the equation for hyperbola,
Equation Of Hyperbola
The figure given below represents a hyperbola whose center is at origin and the major axis is the x-axis. F1 and F2 represent the foci of the hyperbola, let’s say we take a point A(x, y) anywhere on the hyperbola.
We know that the difference of the distance of point A from two foci is given as “2a”.
AF1 – AF2 = 2a
Let’s use Euclid’s distance formula to substitute the values of the distances.
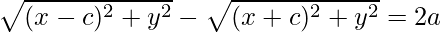
= 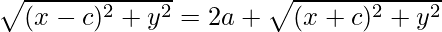
Squaring both sides,
= 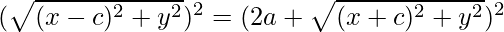
= 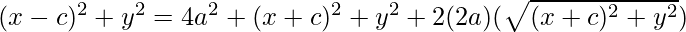
On Simplifying,
= 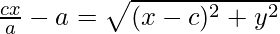
Squaring again,
= 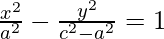
= 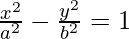
Thus, this is the standard equation for hyperbola.
Latus Rectum
It is a line segment that is perpendicular to the traverse axis and passes through the foci. The endpoints of the latus rectum lie at the intersection between the hyperbola and this line.

Length of the latus rectum in hyperbola is given by, 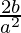
Sample Problems
Question 1: Find the equation of the hyperbola with foci at (2,0) and (-2,0) and the vertices are at (-1,0) and (1,0).
Solution:
Since, the foci lie on the x-axis. We know that the major axis of the hyperbola is x-axis only. So, it is of the form,
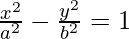
Since the vertices lie at (-1,0) and (1,0), a = 1.
c = 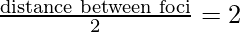
We know that,
c2 = a2 + b2
⇒ 22 = 1 + b2
⇒ 3 = b2
⇒ b = √3
So, the equation of the hyperbola becomes,
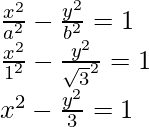
Question 2: Find the equation of the hyperbola with foci at (4,0) and (-4,0) and the vertices are at (-1,0) and (1,0).
Solution:
Since, the foci lie on the x-axis. We know that the major axis of the hyperbola is x-axis only. So, it is of the form,
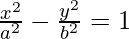
Since the vertices lie at (-1,0) and (1,0), a = 1.
c = 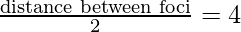
We know that,
c2 = a2 + b2
⇒ 42 = 1 + b2
⇒ 15 = b2
⇒ b = √15
So, the equation of the hyperbola becomes,
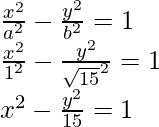
Question 3: Find the equation of the hyperbola with foci at (12,0) and (-12,0) and the length of the latus rectum is 36.
Solution:
Since, the foci lie on the x-axis. We know that the major axis of the hyperbola is x-axis only. So, it is of the form,
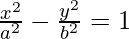
c = 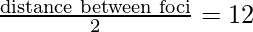
We know that the length of latus rectum is 36.
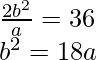
We know,
c2 = a2 + b2
⇒ 122 = a2 + 18a
⇒0 = a2 + 18a – 144
a = -24 and 6.
So, value of a = 6
From the above equations,
b2 = 18 × 6
b = 6√3
So, the equation of the hyperbola becomes,
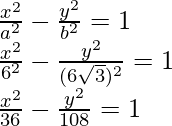
Question 4: Find the equation of the hyperbola with foci at (6,0) and (-6,0) and the length of the latus rectum is 18.
Solution:
Since, the foci lie on the x-axis. We know that the major axis of the hyperbola is x-axis only. So, it is of the form,
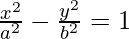
c = 6
We know that the length of latus rectum is 18.
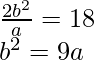
We know,
c2 = a2 + b2
⇒ 62 = a2 + 9a
⇒0 = a2 + 9a – 36
a = – 12 and 3.
So, value of a = 3
From the above equations,
b2 = 3 × 6
b = 3√2
So, the equation of the hyperbola becomes,
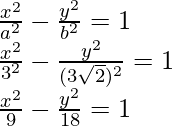
Question 5: Find the center, foci, and the length of the latus rectum for the given hyperbola.
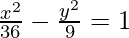
Solution:
We know that this is the standard form the equation for hyperbola, so the center lies at the origin. In this hyperbola,
a = 6 and b = 3.
Length of the latus rectum is given by, 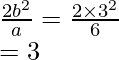
c2 = a2 + b2
c2 = 62 + 32
c2 = 36+ 9
c = √45
The coordinates of foci are (c,0) and (-c,0)
Thus, foci are (√45,0) and (-√45,0).
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...