Sequences and Series
Last Updated :
21 Feb, 2021
In mathematics, the sequence is a collection or list of numbers that have a logical/sequential order or pattern between them. For example, 1, 5, 9, 13, … is a sequence having a difference of 4 between each consecutive next term and each term can be represented in form 1 + 4 * ( n – 1 ) where n is the nth term of the sequence. The sequence can be classified into 3 categories:
- Arithmetic Sequence
- Geometric Sequence
- Harmonic Sequence
Arithmetic Sequence
The sequence in which each consecutive term has a common difference and this difference could be positive, negative and even zero is known as an arithmetic sequence.
Example:
1) 0, 2, 4, 6, … in this sequence each and every consecutive term has a difference of 2 between them and nth term of sequence can be represented as 2 * ( n – 1 ).
2) 0, 5, 10, 15, … is another example of arithmetic sequence with a difference of 5 between each consecutive number and nth term of sequence can be represented as 5 * ( n – 1 ).
Geometric Sequence
The sequence in which each consecutive term has a common ratio is known as a Geometric sequence.
Example:
1) 1, 5, 25, 125 … in this sequence, each consecutive term have a ratio of 5 with the term before it and nth term of sequence can be represented as 5 ( n – 1 ).
2) 1, -2, 4, -8, 16, … in this sequence each consecutive term have a ratio of -2 with the term before it and nth term of sequence can be represented as ( -2 )( n – 1 ).
Harmonic Sequence
The sequence in which the reciprocal of each term forms an arithmetic sequence is known as a harmonic sequence.
Example:
(1/5), (1/10), (1/15), (1/20),… in this sequence the reciprocal of each term that is 5, 10, 15, 20, … forms an arithmetic sequence with a difference of 5 between each consecutive term.
What is Summation Notation?
Summation Notation is a simple method to find the sum of a sequence. Summation notation is also known as sigma notation. Sigma refers to the Greek letter sigma, Σ. The limit of the sequence is represented as shown in figure 1 where the lower limit is the starting index of the sequence and the upper limit represents the ending index of the sequence. Like as shown in figure 1 the lower limit is 1 and the upper limit is 4 so this means we need the sum of 1st,2nd,3rd and 4th term which is ( 2 * 1 ) + ( 2 * 2 ) + ( 2 * 3 ) + ( 2 * 4 ) = 2 + 4 + 6 + 8 = 20.
Summation Notation:
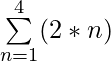
Summation Notation for Arithmetic Sequence
Summation Notation of Arithmetic Sequence is of form Σ (a + b * n) where a is the first term of the sequence and b is the common difference between any two consecutive terms of the sequence and therefore the nth term of the sequence would be of the form (a + (b * n)).
Example:
Let the arithmetic sequence be 0, 2, 4, 6, … so for making the summation notation we need to find the values of ‘a’ and ‘b’ where ‘a’ is the first term which is 0 so a = 0 and b is the common difference between any 2 consecutive terms which is 2 in this case, so b = 2.Therefore summation notion of sequence would be Σ (0 + (2 * n)) where the lower limit is 0 and the upper limit is ∞ as the first term of the sequence is given as 0 and ending is not defined.
Arithmetic Summation Notation:
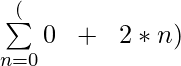
Summation Notation for Geometric Sequence
Summation Notation of Geometric Sequence is of form Σ (a * bn) where a is the first term of the sequence and b is the common ratio between any two consecutive terms of the sequence and therefore the nth term of the sequence would be of the form (a * bn).
Example:
Let the geometric sequence be 2, 10, 50, 250, … so for making the summation notation we need to find the values of ‘a’ and ‘b’ where ‘a’ is the first term which is 2 so a = 2 and b is the common ratio between any 2 consecutive terms which is 5 in this case, so b = 5.Therefore summation notion of sequence would be Σ (2 * 5 n) where the lower limit is 0 and the upper limit is ∞ as the first term of the sequence is given as 0 and ending is not defined.
Geometric Summation Notation:
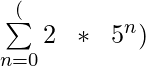
Summation Notation for Harmonic Sequence
Summation Notation of Harmonic Sequence is of form Σ ( 1/(a + b*n) )where a is the reciprocal of the first term of the sequence and b is the common difference between reciprocal any two consecutive terms of the sequence and therefore the nth term of the sequence would be of the form (1/(a + b * n)).
Example:
Let the arithmetic sequence be 1/2, 1/4, 1/6, … so for making the summation notation we need to find the values of ‘a’ and ‘b’ where ‘a’ is the reciprocal first term which is 2 so a = 2 and b is the common difference between the reciprocal of any 2 consecutive terms which is 2 in this case, so b = 2.Therefore summation notion of sequence would be Σ (1/( 0 + 2 * n)) where the lower limit is 1 and the upper limit is ∞ as the first term of the sequence is given as 1/2 and ending is not defined.
Harmonic Summation Notation:
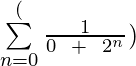
Examples
Example 1: Find the first 4 terms of the sequence: an = 2 * xn + 1 and n > 0?
Solution:
As we should take care to replace n ( and not x ) with the first 4 natural numbers as n is not equal to 0.
a1 = 2 * x1 + 1
a2 = 2 * x2 + 1
a3 = 2 * x3 + 1
a4 = 2 * x4 + 1
Example 2: Find the first 6 terms of the sequence: an = 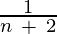 and n ≥ 0?
and n ≥ 0?
Solution:
We have to replace n by the first 6 while numbers (0, 1, 2, 3, 4, 5).
a0 = 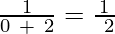
a1 = 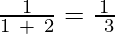
a2 = 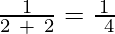
a3 = 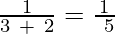
a4 = 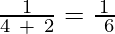
a5 = 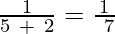
Example 3: Evaluate 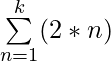 for k = 2 and k = 4?
for k = 2 and k = 4?
Solution:
For k = 2
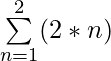 = (2 * 1) + (2 * 2) = 2 + 4 = 6
= (2 * 1) + (2 * 2) = 2 + 4 = 6
For k = 4
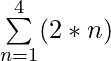 = (2 * 1) + (2 * 2) + (2 * 3) + (2 * 4) = 2 + 4 + 6 + 8 = 20
= (2 * 1) + (2 * 2) + (2 * 3) + (2 * 4) = 2 + 4 + 6 + 8 = 20
Example 4: Evaluate 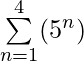 ?
?
Solution:
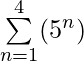 = (51) + (52) + (53) + (54) = 5 + 25 + 125 + 625 = 780
= (51) + (52) + (53) + (54) = 5 + 25 + 125 + 625 = 780
Example 5: Evaluate 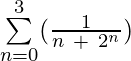 ?
?
Solution:
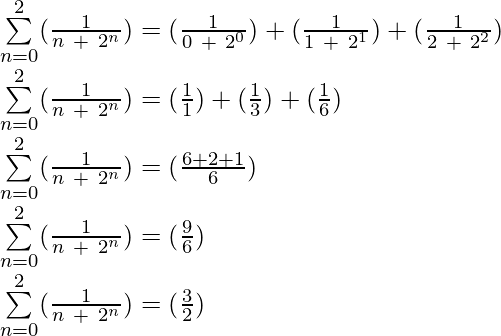
Example 6: Write in expanded form: 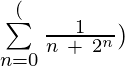 upto 4 terms?
upto 4 terms?
Solution:
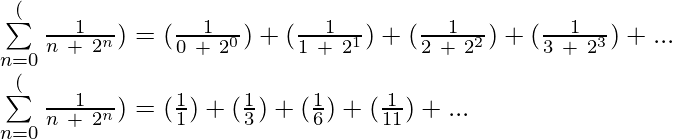
Share your thoughts in the comments
Please Login to comment...