Relation and Function are two ways of establishing links between two sets in mathematics. Relation and Function in maths are analogous to the relation that we see in our daily lives i.e., two persons are related by the relation of father-son, mother-daughter, brother-sister, and many more. On a similar pattern, two numbers can be related to each other as one number is the square of another number and many more. A function is a special kind of relation that is defined as a unique relation between two mathematical entities.
Relation and Functions are introduced in Class 11, and in Class 12 more advanced subtopics are taught in CBSE Syllabus. In this article, we will learn about relation and function, their definitions, relation and function examples, their representation, terms related to them, and the difference between relation and function in detail.
What is Relation and Function?
Relation and Functions are the ways of mapping the establishing link between two entities in mathematics. They are used to establish mathematical relations between two terms. Relation and Function are studied under algebra and also used in calculus to find integration and differentiation.

Let’s learn their definitions separately.
Relation Definition
Relation is defined on a non-empty set A to no-empty set B such that Relation from A to B is a subset of Cartesian Product of A and B i.e. R ⊆ A × B.
For Example if A = {a, b, c} and B = {p, q, r},
Then A × B = {(a, p), (a, q), (a, r), (b, p), (b, q), (b, r), (c, p), (c, q), (c, r)}.
If there is another set are that is defined as R = {(a, p), (b, q), (c, r)} then we see that R is a subset of A × B.
Hence, R is a relation from set A to set B.
Function Defintion
Function is a special type of relation in which the two entities are exclusively related to each other only. A relation from set A to set B is defined as function if all the elements of set A are related to at least one element of B and no two elements of B are related to a single element of A.
Here, the element of set A are called pre-image and the element of set B are called image. Hence a function from A to B is defined only when each pre-image in set A has an image in B and no two different images in B has a single pre-image in A.
It should be noted that every function is a relation but not every relation is a function.

Representation of Relation and Function
Relation and Function are in general the same with some basic difference. They both take input, process it and relates to output. They can be represented in the following forms:
Roster Form
In roster form the elements of two sets among which relation is defined are written in the form of ordered pair.
For Example, if A = {-1, 0, 1, 2} and B = {0, 1, 2, 3, 4} and set A is related to set B as a2 = b where a is an element of set A and b is an element of set B then R = {(-1, 1), (0, 0), (1, 1), (2, 4)}.
Set Builder Form
In set builder form the relation is not written in expanded pair form rather it is written in compressed form using an algebraic expression to define the relation between two sets.
For Example, if A = {-1, 0, 1, 2} and B = {0, 1, 2, 3, 4} and set A is related to set B as a2 = b where a is an element of set A and b is an element of set B then Relation in Set Builder form is given as R = {(a, b): a ϵ A, b ϵ B and b = a2}
Arrow Diagram
In arrow diagram the relation is shown using connecting the elements of the sets which are contained in the box using arrows.
For Example, if A = {-1, 0, 1, 2} and B = {0, 1, 2, 3, 4} and set A is related to set B as a2 = b where a is an element of set A and b is an element of set B then Relation in Arrow Diagram is given as follows:

Lattice Diagram
In lattice diagrams the elements which are linked to each other by a relation are plotted on cartesian plane.
For Example, if A = {-1, 0, 1, -2, 3} and B = {0, 1, 2, 3, 4, 9} and set A is related to set B as a2 = b where a is an element of set A and b is an element of set B then Relation in Lattice Diagram is given as follows.

Some of the commonly used terms associated with Relation and Function are discussed below:
Domain
Domain of Relation or a function is the set of inputs for which the outputs are obtained. For Example, in A = {-1, 0, 1, 2} and B = {0, 1, 2, 3, 4} and set A is related to set B as a2 = b, the set A is the domain of the relation.
Codomain
Codomain is the set of outputs or the image of the relation and function. Codomain may contain exact or more number of elements than the output. For Example, in A = {-1, 0, 1, 2} and B = {0, 1, 2, 3, 4} and set A is related to set B as a2 = b, set B is the codomain. In set B there is element 3 which is not a perfect square hence it will not have a pre-image.
Range
Range is the set of all outputs which has a pre image. In range all elements are related. Hence, it has has exact number of elements for which relation is defined. Thus, Range is subset of codomain. For Example, in A = {-1, 0, 1, 2} and B = {0, 1, 2, 3, 4} and set A is related to set B as a2 = b, Range is {0, 1, 2, 4}.
Cartesian Product
Let’s assume A and B to be two non-empty sets, the sets of all ordered pairs (x, y) where x ∈ A and y ∈ B is called a Cartesian product of the sets. A × B = {(x, y) | x ∈ A and y ∈ B}
Learn More, Domain and Range of Relation and Function
Types of Relation and Function
Relation and Function are classified on the basis of the input it take and output it gives for a given relation. The different types of Relation and Function are discussed separately below:
Types of Relation
There are eight different types of relations which are listed below:
- Empty Relation- There is no relation between any elements of a set.
- Universal Relation- Every element of the set is related to each other.
- Identity Relation- In an identity relation, every element of a set is related to itself only.
- Inverse Relation- Inverse relation is seen when a set has elements that are inverse pairs of another set.
- Reflexive Relation- In a reflexive relation, every element maps to itself.
- Symmetric Relation- In asymmetric relation, if a=b is true then b=a is also true.
- Transitive Relation- For transitive relation, if (x, y) ∈ R, (y, z) ∈ R, then (x, z) ∈ R.
- Equivalence Relation- A relation that is symmetric, transitive, and reflexive at the same time.
Learn more about Types of Relation.
Types of Function
We know that in a function no two images can have one common pre-image and all the pre-images must have an image. A function ‘f’ defined from A × B is classified as follows
- One-One Function(Injection): A function ‘f’ from A to B is said to be One-One or Injection if each element of A is mapped with a different element in B. One-One Function is also called an Injective Function.
- Many-One Function: A function ‘f’ from A to B is said to be Many-One or Injection if two or more elements of A is mapped with a common element in B. It means two elemts in A can have common image in B.
- Onto Function(Surjection): A function ‘f’ from A to B is said to be Onto Function if all the elements of set B has a pre-image in set A i.e. no element in set B remains unmapped.
- Into Function: A function ‘f’ from A to B is said to be Into Function if at least one image in set B does not have a pre-image in set A i.e. one element of set B remains unmapped.
- One-One Onto Function: A function ‘f’ from A to B is said to be One-One Onto function if all the elements of set A has a unique image in set B and all the elements of set B has a pre-image in set A. This type of function exhibits characteristics of One One Function and Onto Function. One-One Onto Function is also called Bijection Function.
Apart from the above types of function there are other standard functions such as constant function, algebraic function, greatest integer function, logarithmic function and trigonometric function etc which can be studied from the link attached below:
Learn More, Types of Function
Difference Between Relation and Function
Relation and Function are basically the same but they differ from each other in some manner. Let’s understand the difference between them from the table given below:
|
| Relation is defined a non-empty set A to non-empty set B such that Relation from A to B is a subset of A × B i.e. R ⊆ A × B | Function is a special type of relation from set A to set B where all the elements of set A are related to some or all elements of set B and no two elements of set B is related to a common element in set A. |
| In case of relation of the pre-image may or may not have an image | In case of function all pre-image must have an image |
| In case of relation a pre-image can have two or more image | In case of function no two image can have a common pre-image |
| A relation can or can not be a function | A function is always a relation. |
Read More,
Relation and Function Examples
Example 1: Find the cartesian products of set A = {1, 2, 3} and B={3, 4, 5}.
Solution:
Following the above definition, let Cartesian product be R,
R = A ⨯ B
= {(1,3), (1,4), (1,5), (2,3), (2,4), (2,5), (3,3), (3,4), (3,5)}
Example 2: Verify if ƒ(x) = x2 is a function or not.
Solution:
Here, the function takes a number as input. So its domain is all real numbers and in the output it gives the square of that number as output. So the co-domain will be all the positive numbers.
Now, according to the definition of Function for each element of domain, it should give a unique output but vice versa is not true.
For example: here, x = -2 and 2 both give the same output 4.
Since the condition is not violated, it will be considered as a function.
Example 3: A relation is given in the table below, find out whether this relation is a function or not.
Answer:
In the above table the elements 1 and 3 in the image column i.e. have a common pre-image 2 which violates the definition of function that no two or more images can have a common pre image. Hence, the given relation is not a function.
Example 4: A relation is given in the table below, find out whether this relation is a function or not.
Answer:
In the above relation, each input has only one corresponding range value. So, this relation is a function.
Example 5: Find out the range of function: ƒ(x) = 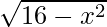
Solution:
Since the value inside the root cannot be negative, x2 should be less than 16.
That means x ∈ [-4,4]. This is domain of the function.
For the range, let y= then y2 = 16 – x2
then y2 = 16 – x2
or x2= 16 – y2
Since x ∈ [– 4, 4]
Thus range of f = [0, 4]
Example 6: Plot the graph of function f(x) = |x|.
Solution:
The above function is a modulus function. In case of modulus function, f(x) = x if x > 0 and -x otherwise. The graph for the same is given below:

It can be noticed that in this, there are multiple inputs mapping to same value of the function. For Example: x = -2 and x = 2 both give f(x) = 2.
FAQs on Relation and Function
1. Define Relation and Function.
Relation is defined between two non-empty set A and B such that Relation is a subset of A ⨯ B. Function is defined as a special relation where element of set A is uniquely related to elements of set B.
2. What is Domain of Relation and Function?
Domain of Relation and Function is the set of input which gives an output when undergoes a relation. Domain can also be considered as pre-image.
3. What is Range of Relation and Function?
Range of Relation and Function is the set of output obtained when domain undergoes a relation.
4. What is the Relation between Codomain and Range?
The relation between Codomain and Range is that the Range is a subset of Codomain.
5. How to Represent Relation and Function?
Relation and Function can be represented using Roaster Form, Set-Builder Form, Arrow Form and Lattice Form. The details have been discussed under the topic above in the article.
6. What is the Difference between Relation and Function?
The basic difference between Relation and Function is that in Relation pre-image can be unmapped and two or more image can have same pre-image while in case of Function the all the pre-image must have an image and no two or more image can have the same pre-image.
Share your thoughts in the comments
Please Login to comment...