Algebraic Operations on Complex Numbers | Class 11 Maths
Last Updated :
04 Dec, 2020
A complex number is a number that can be expressed in the form a + bi, where a and b are real numbers, and i represents the imaginary unit, satisfying the equation i² = −1. For example, 5+6i is a complex number, where 5 is a real number and 6i is an imaginary number. Therefore, the combination of both the real number and imaginary number is a complex number. There can be four types of algebraic operations on complex numbers which are mentioned below. The four operations on the complex numbers include:
- Addition
- Subtraction
- Multiplication
- Division
Addition of Complex Numbers
To add two complex numbers, just add the corresponding real and imaginary parts.
(a + bi) + (c + di) = (a + c) + (b + d)i
Examples:
- (7 + 8i) + (6 + 3i) = (7 + 6) + (8 + 3)i = 13 + 11i
- (2 + 5i) + (13 + 7i) = (2 + 13) + (7 + 5)i = 15 + 12i
- (-3 – 6i) + (-4 + 14i) = (-3 – 4) + (-6 + 14)i = -7 + 8i
- (4 – 3i ) + ( 6 + 3i) = (4+6) + (-3+3)i = 10
- (6 + 11i) + (4 + 3i) = (4 + 6) + (11 + 3)i = 10 + 14i
Subtraction of Complex Numbers
To subtract two complex numbers, just subtract the corresponding real and imaginary parts.
(a + bi) − (c + di) = (a − c) + (b − d)i
Examples:
- (6 + 8i) – (3 + 4i) = (6 – 3) + (8 – 4)i = 3 + 4i
- (7 + 15i) – (2 + 5i) = (7 – 2) + (15 – 5)i = 5 + 10i
- (-3 + 5i) – (6 + 9i) = (-3 – 6) + (5 – 9)i = -9 – 4i
- (14 – 3i) – (-7 + 2i) = (14 – (-7)) + (-3 – 2)i = 21 – 5i
- (-2 + 6i) – (4 + 13i) = (-2 – 4) + (6 – 13)i = -6 – 7i
Multiplication of Two Complex Numbers
Multiplication of two complex numbers is the same as the multiplication of two binomials. Let us suppose that we have to multiply a + bi and c + di. We will multiply them term by term.
(a + bi) ∗ (c + di) = (a + bi) ∗ c + (a + bi) ∗ di
= (a ∗ c + (b ∗ c)i)+((a ∗ d)i + b ∗ d ∗ −1)
= (a ∗ c − b ∗ d + i(b ∗ c + a ∗ d))
Example 1: Multiply (1 + 4i) and (3 + 5i).
(1 + 4i) ∗ (3 + 5i) = (3 + 12i) + (5i + 20i2)
= 3 + 17i − 20
= −17 + 17i
Note: Multiplication of complex numbers with real numbers or purely imaginary can be done in the same manner.
Example 2: Multiply 5 and (4 + 7i).
5 ∗ (4+7i) can be viewed as (5 + 0i) ∗ (4 + 7i)
= 5 ∗ (4 + 7i)
= 20 + 35i
Example 3: Multiply 3i and (2 + 6i).
3i ∗ (2 + 6i) can be viewed as (0 + 3i) ∗ (2 + 6i)
= 3i ∗ (2 + 6i)
= 6i + 18i2
= 6i − 18
= −18 + 6i
Example 4: Multiply (5 + 3i) and (3 + 4i).
(5+3i) ∗ (3+4i) = (5 + 3i) ∗ 3 + (5 + 3i) ∗ 4i
= (15 + 9i) + (20i + 12i2)
= (15 − 12) + (20 + 9)i
= 3 + 29i
Review of Complex Numbers Addition, Subtraction and Multiplication
- (a + bi) + (c + di) = (a + c) + (b + d)i
- (a + bi) − (c + di) = (a − c) + (b − d)i
- (a + bi) ∗ (c + di) = ((a ∗ c − b ∗ d) + (b ∗ c + a ∗ d)i)
Conjugate of a Complex Number
In any two complex numbers, if only the sign of the imaginary part differs then, they are known as a complex conjugate of each other. Thus conjugate of a complex number a + bi would be a – bi.
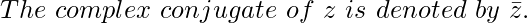
What’s the use of a complex conjugate?

Thus we can observe that multiplying a complex number with its conjugate gives us a real number. Thus the division of complex numbers is possible by multiplying both numerator and denominator with the complex conjugate of the denominator.
Examples of Complex Conjugates
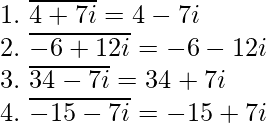
Properties of Complex Conjugates
Property 1:
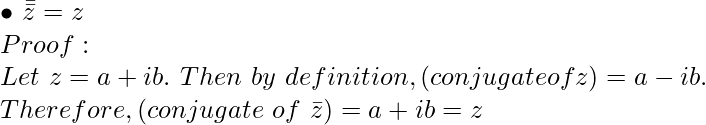
Property 2:
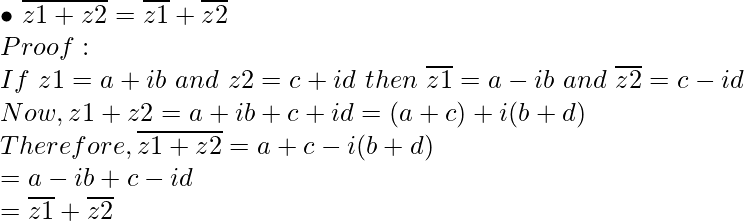
Property 3:
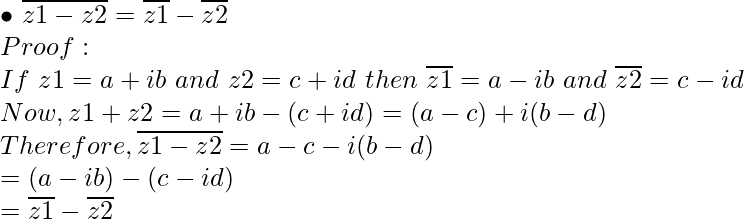
Property 4:

Property 5:
![Rendered by QuickLaTeX.com { \bullet } \ \overline {(\frac{z1}{z2})} = \frac{\overline {z1}}{\overline {z2}} ,\ provided\ z2\neq 0 \\ Proof: \\ According\ to\ the\ problem \\ z2 ≠ 0 ⇒ \overline {z2} ≠ 0 \\ Let, \frac{z1}{z2} = z3 \\ z1 = z2*z3 \\ ⇒ \overline {z1} = \overline {z2*z3} \\ ⇒ \overline {z1} = \overline {z2}*\overline {z3} \\ ⇒ \frac{\overline {z1}}{\overline {z2}} = \overline {z3} \\ \ \\ ⇒ \overline {(\frac{z1}{z2})} = \frac{\overline {z1}}{\overline {z2}}, [Since\ z3 = \frac{z1}{z2}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-4c84d4206ce9e918f0ec787e778a715c_l3.png)
Division of Two Complex Numbers
Division of complex numbers is done by multiplying both numerator and denominator with the complex conjugate of the denominator.

Example 1:

Example 2:
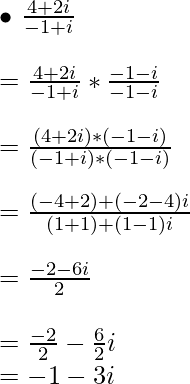
Example 3:
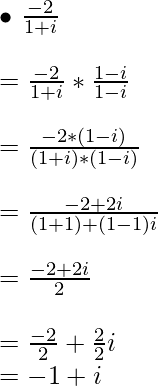
Example 4:
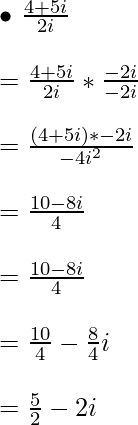
Share your thoughts in the comments
Please Login to comment...