In a cricket match, before the game begins. Two captains go for a toss. Tossing is an activity of flipping a coin and checking the result as either “Head” or “Tail”. Similarly, tossing a die gives us a number from 1 to 6. All these activities are examples of experiments. An activity that gives us a result is called an experiment. There are can be more than one outcome of an experiment. The field of probability is more concerned with random experiments. These experiments do not have a definite outcome, that is you cannot predict the outcome of these experiments with absolute certainty.
Experiments
Probability theory is based on experiments. An experiment is a test, trial, or procedure for the purpose of discovering something unknown, testing a principle or supposition, etc. Following is the list of some activities that can be considered as experiments:
- Toss the coin repeatedly and note the outcomes. There are two possible outcomes – Head(H) or Tails(T).
- Throwing a fair die and observing the number it gives as a result.
- Driving from Delhi to Bangalore and measuring the distance between the two cities.
All the activities listed above can be described as experiments. Notice that in activity 1 and activity 2 we do not know the result of the activity and cannot say with certainty what number will appear on-die or whether we will get a head or tails with the coin toss. The result of activity 3 can be predicted easily. This means that there is randomness involved in experiment-1 and 2. Such experiments are called random experiments.
Random Experiments
The underlying assumption of the probability theory is that the experiments must be random. It is assumed that the experiment can be performed infinitely many times under the same conditions. This assumption becomes important because both classical probability theory and frequency-based probability theory relies on this assumption as it looks for the long-term behaviors in the experiments.
A random experiment is defined as an experiment whose outcome cannot be predicted with certainty.
It is impossible to predict the result when a die is rolled. This is an example of a random experiment. Each random experiment must fulfill the following two conditions:
- The experiment can be repeated a number of times under the same conditions.
- The outcome of the experiment cannot be predicted beforehand with certainty.
To illustrate this concept, let’s take this experiment as an example.
A coin is tossed two times and the outcomes are recorded. The possible outcomes are:
HH, HT, TH, TT
The figure below represents the outcomes in form of a tree.
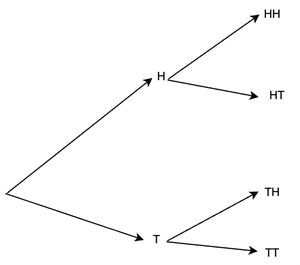
Notice that there are four possible outcomes in this experiment and none of them can be predicted beforehand. The set of all possible outcomes makes up the sample space for the random experiment. Thus, in the context of our experiment, the sample space is a universal set. It is denoted as S. For the above experiment,
S = {HT, HH, TH, TT}
When an experiment is repeated several times, each one of them is called a trial. Thus, a trial can be described as a particular performance of a random experiment. In this particular experiment, a trial is the tossing of the coin. Two such trials constitute the whole experiment.
Events and Probabilities
For an experiment with sample space S, the goal is to assign probabilities to certain outcomes. To understand the concept of events, let’s consider an experiment again. Two dice are rolled, we are interested in the outcomes where the sum of the numbers of dice is equal to 6. The first step is to consider the sample space for this experiment.
S = {(1,1); (1,2); …..(1, 6);
(2,1); (2,2); … (2,6);
(3,1); (3,2); ….(3,6);
(4,1); (4,2); …..(4,6);
(5,1); (5,2); ……(5,6);
(6,1); (6,2); ……(6,6); }
These are all the possible outcomes of this experiment.
An event is the subset of the sample space.
In this case, the event will be the outcomes where the sum of the number on the dice is equal to 6. It will contain all those outcomes from the set S, where the sum of the numbers is 6. Let’s say the event is denoted by E,
E = {(2,4); (4,2); (3,3); (3,3); (1,5); (5,1)}
The cardinality of this set |E| = 6 while the cardinality of sample space |S| = 36.
Probability is defined as the ratio of the favorable number of outcomes and total number of possible outcomes
P(Event) = 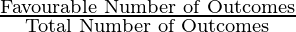
For this case,
P(E) = 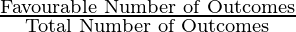
⇒ P(E) = 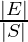
⇒ P(E) = 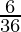
⇒ P(E) = 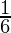
Let’s look at some examples on these concepts.
Sample Problems
Question 1: Write the sample space for three tosses of a coin.
Answer:
A coin toss gives either Head (H) or Tails(T).
Outcome of three coin tosses will be triplets of Heads and Tails.
S = {HHH, HHT, HTH, HTT, THH, THT, TTH, TTT}

Question 2: Out of the following activities given below. Choose random activities:
- Drawing a ball from an urn containing black and white balls.
- Multiplying 4 and 8 on the calculator.
- Birth of a person
Answer:
Each random experiment/activity must fulfill the following two conditions:
- The experiment can be repeated a number of times under the same conditions.
- The outcome of the experiment cannot be predicted beforehand with certainty.
Drawing a ball from an urn containing black and white balls.
This can be repeated as many times as required, and also it cannot be predicted which ball will be drawn. Thus is a random activity.
Multiplying 4 and 8 on the calculator.
This activity can be repeated a number of times, but the result of this activity can be predicted beforehand. Thus, it is not a random activity.
Birth of a person
Birth of a person cannot be repeated. So, it is not a random activity.
Question 3: Consider an experiment of rolling a die and then tossing a coin. Draw the sample space.
Answer:
A die when rolled given {1, 2, 3, 4, 5, 6} as result while a coin toss gives {H, T}.

Sample space S = {(1, H); (2, H); (3, H); (4,H); (5,H); (6,H); (1, T); (2, T); (3, T); (4, T); (5, T); (6, T)}
Question 4: Find the probability of getting 2 heads in three tosses of a coin.
Answer:
A coin toss gives either Head (H) or Tails(T).
Outcome of three coin tosses will be triplets of Heads and Tails. So, the sample space is,
S = {HHH, HHT, HTH, HTT, THH, THT, TTH, TTT}
Counting the number of favorable outcomes, there are three outcomes with two heads.
Probability = 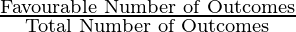
P = 
Question 5: Find the probability of drawing out an ace from a well-shuffled deck of cards.
Answer:
A deck of cards contains 52 cards and out of which 4 are aces. The formula for probability,
Probability = 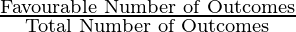
Favorable Number of Outcomes = 4
Total Number of Outcomes = 52
Probability = 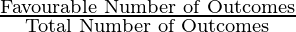
⇒ P = 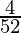
⇒ P = 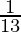
Question 6: Find the probability of getting at least 1 head in three tosses of a coin.
Answer:
A coin toss gives either Head (H) or Tails(T).
Outcome of three coin tosses will be triplets of Heads and Tails. So, the sample space is,
S = {HHH, HHT, HTH, HTT, THH, THT, TTH, TTT}
Counting the number of favorable outcomes, there are seven outcomes with atleast one head.
Probability = 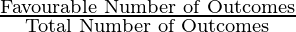
P = 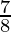
Share your thoughts in the comments
Please Login to comment...