In a plane, we know that we need two mutually perpendicular lines to locate the position of a point. These lines are called coordinate axes of the plane and the plane are usually called the Cartesian plane. But in real life, we do not have such a plane. In real life, to locate objects we need some extra information that as height. So now we need three things to locate a point in real life — x, y, and its height which is usually denoted by z. These are called coordinates with respect to three-dimensional space.
Coordinate Axes and Coordinate Planes
In the figure, we can see three planes intersecting each other. These planes are mutually perpendicular to each other. Lines XOX’, Y’OY and Z’OZ represent the intersection of all the planes with each other. These lines are called the x-axis, y-axis, and z-axis respectively, and they make the 3D rectangular coordinate system.

Coordinate Planes
The planes XOY, YOZ, and ZOX are called XY-plane, YZ-plane, and ZX-plane respectively. The intersection of all the planes is called the origin. These planes divide the 3-D space into 8 octants.
Coordinates of a Point in Space
Any point in 3D space is assumed to have three coordinates denoting the values of x, y, and z coordinates. In the figure below, we are given a point A(x, y, z) located in space. We drop a perpendicular from A to the x-y plane to the point M. The length of AM gives us the value of coordinate z. In the figure, LM and OL give us the value of the y and x coordinate.

Thus, to any point that is present in the space, there exists an ordered triplet (x, y, z) which gives the position of that point in the space.
Coordinates of the origin are (0, 0, 0). A point on x-axis is of the form (x, 0, 0), same goes for the points on y-axis and z-axis.
Distance between Two Points
Let’s say we have two points (x1, y1, z1) and (x2, y2, z2) in the 3-D space. The formula for calculating the distance between two points in 3-D space is similar to Euclid’s formula for the distance we have studied for 2-D space. This formula is a slight modification over the original formula that was given by Euclid.
The distance between two points (x1, y1, z1) and (x2, y2, z2) is given by,
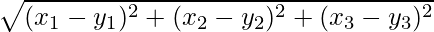
Plane
A plane is a 2-dimensional flat surface that extended infinitely far. It is a 3-dimensional analogous to a line 2-dimensions and a point in a one-dimensional space. It is hard to draw a plane, if we are writing something on paper, it is also a plane. We are writing on a plane. The figure below shows a plane in 3-d space.

Let’s say we have a plane, it intersects the x-axis at “a”, y-axis at “b” and the z-axis at “c”. Its equation is given by,
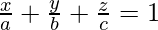

This is called intercept form of the equation of plane.
Sample Problems
Question 1: Let’s say we have a point on the x-axis, what is its y-coordinate and z-coordinate?
Solution:
In the figure, the point lies on x-axis. It can be noticed that it’s coordinates for y and z are equal to zero.

Question 2: Fill in the blanks:
- X and Y axis together make _____ plane.
- All the coordinate planes divide the 3d space into _______ octants.
Answer:
1. X and Y axis together make XY plane.
2. All the coordinates planes divide the 3-D space into eight octants.
Question 3: Calculate the distance between (0,0,0) and (5,4,3).
Solution:
For the points (x1, y1, z1) and (x2, y2, z2)
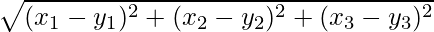
Here, (x1, y1, z1) = (0,0,0) and (x2, y2, z2) = (5,,4,3). Let the distance be “l”
l = 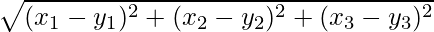
= 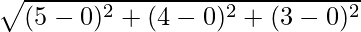
= 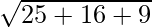
= 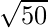
= 5√2
Question 4: Calculate the distance between (0,0,0) and (1,2,3).
Solution:
For the points (x1, y1, z1) and (x2, y2, z2)
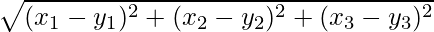
Here, (x1, y1, z1) = (0,0,0) and (x2, y2, z2) = (1,2,3). Let the distance be “l”
l = 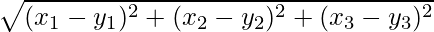
= 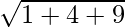
= 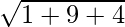
= 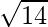
Question 5: Calculate the distance between (1,1,1) and (2,4,3).
Solution:
For the points (x1, y1, z1) and (x2, y2, z2)
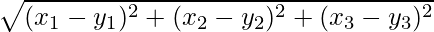
Here, (x1, y1, z1) = (1,1,1) and (x2, y2, z2) = (2,4,3). Let the distance be “l”
l = 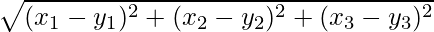
= 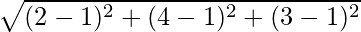
= 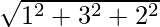
= 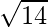
Question 6: In the figure given below, find the equation of the plane.

Solution:
We know the intercept form of an equation of a plane. Let’s say we have a plane, it intersects the x-axis at “a”, y-axis at “b” and the z-axis at “c”. It’s equation is given by,
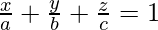
Notice in the figure, a = 5, b = 4 and c = 3
So, the equation of the plane becomes,
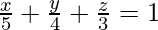
= 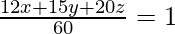
= 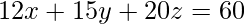
Share your thoughts in the comments
Please Login to comment...