R – Matrices

Matrix is a rectangular arrangement of numbers in rows and columns. In a matrix, as we know rows are the ones that run horizontally and columns are the ones that run vertically. In R programming, matrices are two-dimensional, homogeneous data structures. These are some examples of matrices:

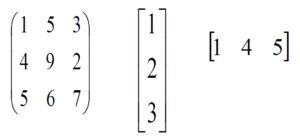
R – Matrices

Creating a Matrix

To create a matrix in R you need to use the function called matrix(). The arguments to this matrix() are the set of elements in the vector. You have to pass how many numbers of rows and how many numbers of columns you want to have in your matrix.

Note: By default, matrices are in column-wise order.

R

# R program to create a matrix

A = matrix(

  # Taking sequence of elements
  c(1, 2, 3, 4, 5, 6, 7, 8, 9),

  # No of rows
  nrow = 3,

  # No of columns
  ncol = 3,

  # By default matrices are in column-wise order
  # So this parameter decides how to arrange the matrix
  byrow = TRUE
)

# Naming rows
rownames(A) = c("a", "b", "c")

# Naming columns
colnames(A) = c("c", "d", "e")

cat("The 3x3 matrix:\n")
print(A)

Output:

The 3x3 matrix:
  c d e
a 1 2 3
b 4 5 6
c 7 8 9

Creating special matrices

R allows the creation of various different types of matrices with the use of arguments passed to the matrix() function.

• Matrix where all rows and columns are filled by a single constant ‘k’:
  To create such a R matrix the syntax is given below:

Syntax: matrix(k, m, n)
Parameters:
k: the constant 
m: no of rows 
n: no of columns 

Example:

R

# R program to illustrate
# special matrices

# Matrix having 3 rows and 3 columns
# filled by a single constant 5
print(matrix(5, 3, 3))

Output:

     [,1] [,2] [,3]
[1,]    5    5    5
[2,]    5    5    5
[3,]    5    5    5

• Diagonal matrix:
  A diagonal matrix is a matrix in which the entries outside the main diagonal are all zero. To create such a R matrix the syntax is given below:

Syntax: diag(k, m, n)
Parameters:
k: the constants/array 
m: no of rows 
n: no of columns  

Example:

R

# R program to illustrate
# special matrices

# Diagonal matrix having 3 rows and 3 columns
# filled by array of elements (5, 3, 3)
print(diag(c(5, 3, 3), 3, 3))

Output:

     [,1] [,2] [,3]
[1,]    5    0    0
[2,]    0    3    0
[3,]    0    0    3

• Identity matrix:
  An identity matrix in which all the elements of the principal diagonal are ones and all other elements are zeros. To create such a R matrix the syntax is given below:

Syntax: diag(k, m, n)
Parameters:
k: 1 
m: no of rows 
n: no of columns 

Example:

R

# R program to illustrate
# special matrices

# Identity matrix having
# 3 rows and 3 columns
print(diag(1, 3, 3))

Output:

     [,1] [,2] [,3]
[1,]    1    0    0
[2,]    0    1    0
[3,]    0    0    1

Matrix metrics

Matrix metrics mean once a matrix is created then 

• How can you know the dimension of the matrix?
• How can you know how many rows are there in the matrix?
• How many columns are in the matrix?
• How many elements are there in the matrix? are the questions we generally wanted to answer.

Example:

R

# R program to illustrate
# matrix metrics

# Create a 3x3 matrix
A = matrix(
  c(1, 2, 3, 4, 5, 6, 7, 8, 9),
  nrow = 3,
  ncol = 3,
  byrow = TRUE
)
cat("The 3x3 matrix:\n")
print(A)

cat("Dimension of the matrix:\n")
print(dim(A))

cat("Number of rows:\n")
print(nrow(A))

cat("Number of columns:\n")
print(ncol(A))

cat("Number of elements:\n")
print(length(A))
# OR
print(prod(dim(A)))

Output:

The 3x3 matrix:
     [,1] [,2] [,3]
[1,]    1    2    3
[2,]    4    5    6
[3,]    7    8    9
Dimension of the matrix:
[1] 3 3
Number of rows:
[1] 3
Number of columns:
[1] 3
Number of elements:
[1] 9
[1] 9

Accessing elements of a Matrix

We can access elements in the R matrices using the same convention that is followed in data frames. So, you will have a matrix and followed by a square bracket with a comma in between array. Value before the comma is used to access rows and value that is after the comma is used to access columns. Let’s illustrate this by taking a simple R code.

Accessing rows:

R

# R program to illustrate
# access rows in metrics

# Create a 3x3 matrix
A = matrix(
  c(1, 2, 3, 4, 5, 6, 7, 8, 9),
  nrow = 3,
  ncol = 3,
  byrow = TRUE
)
cat("The 3x3 matrix:\n")
print(A)

# Accessing first and second row
cat("Accessing first and second row\n")
print(A[1:2, ])

Output:

The 3x3 matrix:
     [, 1] [, 2] [, 3]
[1, ]    1    2    3
[2, ]    4    5    6
[3, ]    7    8    9

Accessing first and second row
     [, 1] [, 2] [, 3]
[1, ]    1    2    3
[2, ]    4    5    6

Accessing columns:

R

# R program to illustrate
# access columns in metrics

# Create a 3x3 matrix
A = matrix(
  c(1, 2, 3, 4, 5, 6, 7, 8, 9),
  nrow = 3,
  ncol = 3,
  byrow = TRUE
)
cat("The 3x3 matrix:\n")
print(A)

# Accessing first and second column
cat("Accessing first and second column\n")
print(A[, 1:2])

Output:

The 3x3 matrix:
     [, 1] [, 2] [, 3]
[1, ]    1    2    3
[2, ]    4    5    6
[3, ]    7    8    9

Accessing first and second column
     [, 1] [, 2]
[1, ]    1    2
[2, ]    4    5
[3, ]    7    8

Accessing elements of a R matrix:

R

# R program to illustrate
# access an entry in metrics

# Create a 3x3 matrix
A = matrix(
  c(1, 2, 3, 4, 5, 6, 7, 8, 9),
  nrow = 3,
  ncol = 3,
  byrow = TRUE
)
cat("The 3x3 matrix:\n")
print(A)

# Accessing 2
print(A[1, 2])

# Accessing 6
print(A[2, 3])

Output:

The 3x3 matrix:
     [, 1] [, 2] [, 3]
[1, ]    1    2    3
[2, ]    4    5    6
[3, ]    7    8    9

[1] 2
[1] 6

Accessing Submatrices:

We can access the submatrix in a matrix using the colon(:) operator. 

R

# R program to illustrate
# access submatrices in a matrix

# Create a 3x3 matrix
A = matrix(
  c(1, 2, 3, 4, 5, 6, 7, 8, 9),
  nrow = 3,
  ncol = 3,
  byrow = TRUE
)
cat("The 3x3 matrix:\n")
print(A)

cat("Accessing the first three rows and the first two columns\n")
print(A[1:3, 1:2])

Output:

The 3x3 matrix:
     [, 1] [, 2] [, 3]
[1, ]    1    2    3
[2, ]    4    5    6
[3, ]    7    8    9

Accessing the first three rows and the first two columns
     [, 1] [, 2]
[1, ]    1    2
[2, ]    4    5
[3, ]    7    8

Modifying Elements of a Matrix

In R you can modify the elements of the matrices by a direct assignment. 

Example:

R

# R program to illustrate
# editing elements in metrics

# Create a 3x3 matrix
A = matrix(
  c(1, 2, 3, 4, 5, 6, 7, 8, 9),
  nrow = 3,
  ncol = 3,
  byrow = TRUE
)
cat("The 3x3 matrix:\n")
print(A)

# Editing the 3rd rows and 3rd column element
# from 9 to 30
# by direct assignments
A[3, 3] = 30

cat("After edited the matrix\n")
print(A)

Output:

The 3x3 matrix:
     [, 1] [, 2] [, 3]
[1, ]    1    2    3
[2, ]    4    5    6
[3, ]    7    8    9

After edited the matrix
     [, 1] [, 2] [, 3]
[1, ]    1    2    3
[2, ]    4    5    6
[3, ]    7    8   30

Matrix Concatenation

Matrix concatenation refers to the merging of rows or columns of an existing R matrix. 

Concatenation of a row:

The concatenation of a row to a matrix is done using rbind(). 

R

# R program to illustrate
# concatenation of a row in metrics

# Create a 3x3 matrix
A = matrix(
  c(1, 2, 3, 4, 5, 6, 7, 8, 9),
  nrow = 3,
  ncol = 3,
  byrow = TRUE
)
cat("The 3x3 matrix:\n")
print(A)

# Creating another 1x3 matrix
B = matrix(
  c(10, 11, 12),
  nrow = 1,
  ncol = 3
)
cat("The 1x3 matrix:\n")
print(B)

# Add a new row using rbind()
C = rbind(A, B)

cat("After concatenation of a row:\n")
print(C)

Output:

The 3x3 matrix:
     [, 1] [, 2] [, 3]
[1, ]    1    2    3
[2, ]    4    5    6
[3, ]    7    8    9

The 1x3 matrix:
     [, 1] [, 2] [, 3]
[1, ]   10   11   12

After concatenation of a row:
     [, 1] [, 2] [, 3]
[1, ]    1    2    3
[2, ]    4    5    6
[3, ]    7    8    9
[4, ]   10   11   12

Concatenation of a column:

The concatenation of a column to a matrix is done using cbind(). 

R

# R program to illustrate
# concatenation of a column in metrics

# Create a 3x3 matrix
A = matrix(
  c(1, 2, 3, 4, 5, 6, 7, 8, 9),
  nrow = 3,
  ncol = 3,
  byrow = TRUE
)
cat("The 3x3 matrix:\n")
print(A)

# Creating another 3x1 matrix
B = matrix(
  c(10, 11, 12),
  nrow = 3,
  ncol = 1,
  byrow = TRUE
)
cat("The 3x1 matrix:\n")
print(B)

# Add a new column using cbind()
C = cbind(A, B)

cat("After concatenation of a column:\n")
print(C)

Output:

The 3x3 matrix:
     [, 1] [, 2] [, 3]
[1, ]    1    2    3
[2, ]    4    5    6
[3, ]    7    8    9

The 3x1 matrix:
     [, 1]
[1, ]   10
[2, ]   11
[3, ]   12

After concatenation of a column:
     [, 1] [, 2] [, 3] [, 4]
[1, ]    1    2    3   10
[2, ]    4    5    6   11
[3, ]    7    8    9   12

Dimension inconsistency: Note that you have to make sure the consistency of dimensions between the matrix before you do this matrix concatenation. 

R

# R program to illustrate
# Dimension inconsistency in metrics concatenation

# Create a 3x3 matrix
A = matrix(
  c(1, 2, 3, 4, 5, 6, 7, 8, 9),
  nrow = 3,
  ncol = 3,
  byrow = TRUE
)
cat("The 3x3 matrix:\n")
print(A)

# Creating another 1x3 matrix
B = matrix(
  c(10, 11, 12),
  nrow = 1,
  ncol = 3,
)
cat("The 1x3 matrix:\n")
print(B)

# This will give an error
# because of dimension inconsistency
C = cbind(A, B)

cat("After concatenation of a column:\n")
print(C)

Output:

The 3x3 matrix:
     [, 1] [, 2] [, 3]
[1, ]    1    2    3
[2, ]    4    5    6
[3, ]    7    8    9

The 1x3 matrix:
     [, 1] [, 2] [, 3]
[1, ]   10   11   12

Error in cbind(A, B) : number of rows of matrices must match (see arg 2)

Deleting rows and columns of a Matrix

To delete a row or a column, first of all, you need to access that row or column and then insert a negative sign before that row or column. It indicates that you had to delete that row or column. 

Row deletion:

R

# R program to illustrate
# row deletion in metrics

# Create a 3x3 matrix
A = matrix(
  c(1, 2, 3, 4, 5, 6, 7, 8, 9),
  nrow = 3,
  ncol = 3,
  byrow = TRUE
)
cat("Before deleting the 2nd row\n")
print(A)

# 2nd-row deletion
A = A[-2, ]

cat("After deleted the 2nd row\n")
print(A)

Output:

Before deleting the 2nd row
     [, 1] [, 2] [, 3]
[1, ]    1    2    3
[2, ]    4    5    6
[3, ]    7    8    9

After deleted the 2nd row
     [, 1] [, 2] [, 3]
[1, ]    1    2    3
[2, ]    7    8    9

Column deletion:

R

# R program to illustrate
# column deletion in metrics

# Create a 3x3 matrix
A = matrix(
  c(1, 2, 3, 4, 5, 6, 7, 8, 9),
  nrow = 3,
  ncol = 3,
  byrow = TRUE
)
cat("Before deleting the 2nd column\n")
print(A)

# 2nd-row deletion
A = A[, -2]

cat("After deleted the 2nd column\n")
print(A)

Output:

Before deleting the 2nd column
     [, 1] [, 2] [, 3]
[1, ]    1    2    3
[2, ]    4    5    6
[3, ]    7    8    9

After deleted the 2nd column
     [, 1] [, 2]
[1, ]    1    3
[2, ]    4    6
[3, ]    7    9