Matrices in R are a bunch of values, either real or complex numbers, arranged in a group of fixed number of rows and columns. Matrices are used to depict the data in a structured and well-organized format. It is necessary to enclose the elements of a matrix in parentheses or brackets. A matrix with 9 elements is shown below. 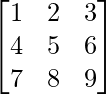 This Matrix [M] has 3 rows and 3 columns. Each element of matrix [M] can be referred to by its row and column number. For example, a23 = 6 Order of a Matrix : The order of a matrix is defined in terms of its number of rows and columns. Order of a matrix = No. of rows × No. of columns Therefore Matrix [M] is a matrix of order 3 × 3.
This Matrix [M] has 3 rows and 3 columns. Each element of matrix [M] can be referred to by its row and column number. For example, a23 = 6 Order of a Matrix : The order of a matrix is defined in terms of its number of rows and columns. Order of a matrix = No. of rows × No. of columns Therefore Matrix [M] is a matrix of order 3 × 3.
Operations on Matrices
There are four basic operations i.e. DMAS (Division, Multiplication, Addition, Subtraction) that can be done with matrices. Both the matrices involved in the operation should have the same number of rows and columns.
Matrices Addition
The addition of two same ordered matrices 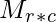 and
and 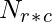 yields a matrix
yields a matrix  where every element is the sum of corresponding elements of the input matrices.
where every element is the sum of corresponding elements of the input matrices.
Python3
B = matrix(c(1, 2, 3, 4, 5, 6), nrow = 2, ncol = 3)
C = matrix(c(7, 8, 9, 10, 11, 12), nrow = 2, ncol = 3)
num_of_rows = nrow(B)
num_of_cols = ncol(B)
sum = matrix(, nrow = num_of_rows, ncol = num_of_cols)
print(B)
print(C)
|
Output:
[,1] [,2] [,3]
[1,] 1 3 5
[2,] 2 4 6
[,1] [,2] [,3]
[1,] 7 9 11
[2,] 8 10 12
[,1] [,2] [,3]
[1,] 8 12 16
[2,] 10 14 18
In the above code, nrow(B) gives the number of rows in B and ncol(B) gives the number of columns. Here, sum is an empty matrix of the same size as B and C. The elements of sum are the addition of the corresponding elements of B and C through nested for loops. Using ‘+’ operator for matrix addition: Similarly, the following R script uses the in-built operator +:
Python3
B = matrix(c(1, 2 + 3i, 5.4, 3, 4, 5), nrow = 2, ncol = 3)
C = matrix(c(2, 0i, 0.1, 3, 4, 5), nrow = 2, ncol = 3)
print(B + C)
|
Output:
[,1] [,2] [,3]
[1,] 3+0i 5.5+0i 8+0i
[2,] 2+3i 6.0+0i 10+0i
R provides the basic inbuilt operator to add the matrices. In the above code, all the elements in the resultant matrix are returned as complex numbers, even if a single element of a matrix is a complex number. Properties of Matrix Addition:
- Commutative: B + C = C + B
- Associative: For n number of matrices A + (B + C) = (A + B) + C
- Order of the matrices involved must be same.
Matrices Subtraction
The subtraction of two same ordered matrices 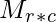 and
and 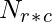 yields a matrix
yields a matrix  where every element is the difference of corresponding elements of the second input matrix from the first.
where every element is the difference of corresponding elements of the second input matrix from the first.
Python3
B = matrix(c(1, 2, 3, 4, 5, 6), nrow = 2, ncol = 3)
C = matrix(c(7, 8, 9, 10, 11, 12), nrow = 2, ncol = 3)
num_of_rows = nrow(B)
num_of_cols = ncol(B)
diff = matrix(, nrow = num_of_rows, ncol = num_of_cols)
print(B)
print(C)
for(row in 1:num_of_rows)
{
for(col in 1:num_of_cols)
{
diff[row, col] <- B[row, col] - C[row, col]
}
}
print(diff)
|
Output:
[,1] [,2] [,3]
[1,] 1 3 5
[2,] 2 4 6
[,1] [,2] [,3]
[1,] 7 9 11
[2,] 8 10 12
[,1] [,2] [,3]
[1,] -6 -6 -6
[2,] -6 -6 -6
Here in the above code, the elements of diff matrix are the subtraction of the corresponding elements of B and C through nested for loops. Using ‘-‘ operator for matrix subtraction: Similarly, the following R script uses the in-built operator ‘-‘:
Python3
B = matrix(c(1, 2 + 3i, 5.4, 3, 4, 5), nrow = 2, ncol = 3)
C = matrix(c(2, 0i, 0.1, 3, 4, 5), nrow = 2, ncol = 3)
print(B - C)
|
Output:
[,1] [,2] [,3]
[1,] -1+0i 5.3+0i 0+0i
[2,] 2+3i 0.0+0i 0+0i
Properties of Matrix Subtraction:
- Non-Commutative: B – C != C – B
- Non-Associative: For n number of matrices A – (B – C) != (A – B) – C
- Order of the matrices involved must be same.
Matrices Multiplication
The multiplication of two same ordered matrices 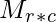 and
and 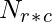 yields a matrix
yields a matrix  where every element is the product of corresponding elements of the input matrices.
where every element is the product of corresponding elements of the input matrices.
Python3
B = matrix(c(1, 2, 3, 4, 5, 6), nrow = 2, ncol = 3)
C = matrix(c(7, 8, 9, 10, 11, 12), nrow = 2, ncol = 3)
num_of_rows = nrow(B)
num_of_cols = ncol(B)
prod = matrix(, nrow = num_of_rows, ncol = num_of_cols)
print(B)
print(C)
for(row in 1:num_of_rows)
{
for(col in 1:num_of_cols)
{
prod[row, col] <- B[row, col] * C[row, col]
}
}
print(prod)
|
Output:
[,1] [,2] [,3]
[1,] 1 3 5
[2,] 2 4 6
[,1] [,2] [,3]
[1,] 7 9 11
[2,] 8 10 12
[,1] [,2] [,3]
[1,] 7 27 55
[2,] 16 40 72
The elements of sum are the multiplication of the corresponding elements of B and C through nested for loops. Using ‘*’ operator for matrix multiplication: Similarly, the following R script uses the in-built operator *:
Python3
B = matrix(c(1, 2 + 3i, 5.4), nrow = 1, ncol = 3)
C = matrix(c(2, 1i, 0.1), nrow = 1, ncol = 3)
print (B * C)
|
Output:
[,1] [,2] [,3]
[1,] 2+0i -3+2i 0.54+0i
Properties of Matrix Multiplication:
- Commutative: B * C = C * B
- Associative: For n number of matrices A * (B * C) = (A * B) * C
- Order of the matrices involved must be same.
Matrices Division
The division of two same ordered matrices 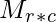 and
and 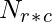 yields a matrix
yields a matrix  where every element is the quotient of corresponding elements of the first matrix element divided by the second.
where every element is the quotient of corresponding elements of the first matrix element divided by the second.
Python3
B = matrix(c(1, 2, 3, 4, 5, 6), nrow = 2, ncol = 3)
C = matrix(c(7, 8, 9, 10, 11, 12), nrow = 2, ncol = 3)
num_of_rows = nrow(B)
num_of_cols = ncol(B)
div = matrix(, nrow = num_of_rows, ncol = num_of_cols)
print(B)
print(C)
for(row in 1:num_of_rows)
{
for(col in 1:num_of_cols)
{
div[row, col] <- B[row, col] / C[row, col]
}
}
print(div)
|
Output:
[,1] [,2] [,3]
[1,] 1 3 5
[2,] 2 4 6
[,1] [,2] [,3]
[1,] 7 9 11
[2,] 8 10 12
[,1] [,2] [,3]
[1,] 0.1428571 0.3333333 0.4545455
[2,] 0.2500000 0.4000000 0.5000000
The elements of div matrix are the division of the corresponding elements of B and C through nested for loops. Using ‘/’ operator for matrix division: Similarly, the following R script uses the in-built operator /:
Python3
B = matrix(c(4, 6i, -1), nrow = 1, ncol = 3)
C = matrix(c(2, 2i, 0), nrow = 1, ncol = 3)
print (B / C)
|
Output:
[,1] [,2] [,3]
[1,] 2+0i 3+0i -Inf+NaNi
Properties of Matrix Division:
- Non-Commutative: B / C != C / B
- Non-Associative: For n number of matrices A / (B / C) != (A / B) / C
- Order of the matrices involved must be same.
Note: Time Complexity of all the matrix operations = O(r*c) where r*c is the order of the matrix.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...