R-matrix is a two-dimensional arrangement of data in rows and columns.
In a matrix, rows are the ones that run horizontally and columns are the ones that run vertically. In R programming, matrices are two-dimensional, homogeneous data structures. These are some examples of matrices:
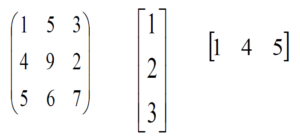
R – Matrices
Creating a Matrix in R
To create a matrix in R you need to use the function called matrix().
The arguments to this matrix() are the set of elements in the vector. You have to pass how many numbers of rows and how many numbers of columns you want to have in your matrix.
Note: By default, matrices are in column-wise order.
Syntax to Create R-Matrix
matrix(data, nrow, ncol, byrow, dimnames)
Parameters:
- data – values you want to enter
- nrow – no. of rows
- ncol – no. of columns
- byrow – logical clue, if ‘true’ value will be assigned by rows
- dimnames – names of rows and columns
Example:
R
A = matrix(
c(1, 2, 3, 4, 5, 6, 7, 8, 9),
nrow = 3,
ncol = 3,
byrow = TRUE
)
rownames(A) = c("a", "b", "c")
colnames(A) = c("c", "d", "e")
cat("The 3x3 matrix:\n")
print(A)
|
Output
The 3x3 matrix:
c d e
a 1 2 3
b 4 5 6
c 7 8 9
Creating Special Matrices in R
R allows the creation of various different types of matrices with the use of arguments passed to the matrix() function.
1. Matrix where all rows and columns are filled by a single constant ‘k’:
To create such a R matrix the syntax is given below:
Syntax: matrix(k, m, n)
Parameters:
k: the constant
m: no of rows
n: no of columns
Example:
Output
[,1] [,2] [,3]
[1,] 5 5 5
[2,] 5 5 5
[3,] 5 5 5
2. Diagonal matrix:
A diagonal matrix is a matrix in which the entries outside the main diagonal are all zero. To create such a R matrix the syntax is given below:
Syntax: diag(k, m, n)
Parameters:
k: the constants/array
m: no of rows
n: no of columns
Example:
R
print(diag(c(5, 3, 3), 3, 3))
|
Output
[,1] [,2] [,3]
[1,] 5 0 0
[2,] 0 3 0
[3,] 0 0 3
3. Identity matrix:
An identity matrix in which all the elements of the principal diagonal are ones and all other elements are zeros. To create such a R matrix the syntax is given below:
Syntax: diag(k, m, n)
Parameters:
k: 1
m: no of rows
n: no of columns
Example:
Output
[,1] [,2] [,3]
[1,] 1 0 0
[2,] 0 1 0
[3,] 0 0 1
4. Matrix Metrics
Matrix metrics tell you about the Matrix you created. You might want to know the number of rows, number of columns, dimensions of a Matrix.
Below Example will help you in answering following questions:
- How can you know the dimension of the matrix?
- How can you know how many rows are there in the matrix?
- How many columns are in the matrix?
- How many elements are there in the matrix?
Example:
R
A = matrix(
c(1, 2, 3, 4, 5, 6, 7, 8, 9),
nrow = 3,
ncol = 3,
byrow = TRUE
)
cat("The 3x3 matrix:\n")
print(A)
cat("Dimension of the matrix:\n")
print(dim(A))
cat("Number of rows:\n")
print(nrow(A))
cat("Number of columns:\n")
print(ncol(A))
cat("Number of elements:\n")
print(length(A))
print(prod(dim(A)))
|
Output
The 3x3 matrix:
[,1] [,2] [,3]
[1,] 1 2 3
[2,] 4 5 6
[3,] 7 8 9
Dimension of the matrix:
[1] 3 3
Number of rows:
[1] 3
Number of columns:
[1] 3
Number of elements:
[1] ...
Accessing Elements of a R-Matrix
We can access elements in the R matrices using the same convention that is followed in data frames. So, you will have a matrix and followed by a square bracket with a comma in between array.
Value before the comma is used to access rows and value that is after the comma is used to access columns. Let’s illustrate this by taking a simple R code.
Accessing rows:
R
A = matrix(
c(1, 2, 3, 4, 5, 6, 7, 8, 9),
nrow = 3,
ncol = 3,
byrow = TRUE
)
cat("The 3x3 matrix:\n")
print(A)
cat("Accessing first and second row\n")
print(A[1:2, ])
|
Output
The 3x3 matrix:
[,1] [,2] [,3]
[1,] 1 2 3
[2,] 4 5 6
[3,] 7 8 9
Accessing first and second row
[,1] [,2] [,3]
[1,] 1 2 3
[2,] 4 5 6
Accessing columns:
R
A = matrix(
c(1, 2, 3, 4, 5, 6, 7, 8, 9),
nrow = 3,
ncol = 3,
byrow = TRUE
)
cat("The 3x3 matrix:\n")
print(A)
cat("Accessing first and second column\n")
print(A[, 1:2])
|
Output
The 3x3 matrix:
[,1] [,2] [,3]
[1,] 1 2 3
[2,] 4 5 6
[3,] 7 8 9
Accessing first and second column
[,1] [,2]
[1,] 1 2
[2,] 4 5
[3,] 7 8
More Example of Accessing Elements of a R-matrix:
R
A = matrix(
c(1, 2, 3, 4, 5, 6, 7, 8, 9),
nrow = 3,
ncol = 3,
byrow = TRUE
)
cat("The 3x3 matrix:\n")
print(A)
print(A[1, 2])
print(A[2, 3])
|
Output
The 3x3 matrix:
[,1] [,2] [,3]
[1,] 1 2 3
[2,] 4 5 6
[3,] 7 8 9
[1] 2
[1] 6
Accessing Submatrices in R:
We can access the submatrix in a matrix using the colon(:) operator.
R
A = matrix(
c(1, 2, 3, 4, 5, 6, 7, 8, 9),
nrow = 3,
ncol = 3,
byrow = TRUE
)
cat("The 3x3 matrix:\n")
print(A)
cat("Accessing the first three rows and the first two columns\n")
print(A[1:3, 1:2])
|
Output
The 3x3 matrix:
[,1] [,2] [,3]
[1,] 1 2 3
[2,] 4 5 6
[3,] 7 8 9
Accessing the first three rows and the first two columns
[,1] [,2]
[1,] 1 2
[2,] 4 5
[3...
Modifying Elements of a R-Matrix
In R you can modify the elements of the matrices by a direct assignment.
Example:
R
A = matrix(
c(1, 2, 3, 4, 5, 6, 7, 8, 9),
nrow = 3,
ncol = 3,
byrow = TRUE
)
cat("The 3x3 matrix:\n")
print(A)
A[3, 3] = 30
cat("After edited the matrix\n")
print(A)
|
Output
The 3x3 matrix:
[,1] [,2] [,3]
[1,] 1 2 3
[2,] 4 5 6
[3,] 7 8 9
After edited the matrix
[,1] [,2] [,3]
[1,] 1 2 3
[2,] 4 5 6
[3,] 7 8 30
R-Matrix Concatenation
Matrix concatenation refers to the merging of rows or columns of an existing R matrix.
Concatenation of a row:
The concatenation of a row to a matrix is done using rbind().
R
A = matrix(
c(1, 2, 3, 4, 5, 6, 7, 8, 9),
nrow = 3,
ncol = 3,
byrow = TRUE
)
cat("The 3x3 matrix:\n")
print(A)
B = matrix(
c(10, 11, 12),
nrow = 1,
ncol = 3
)
cat("The 1x3 matrix:\n")
print(B)
C = rbind(A, B)
cat("After concatenation of a row:\n")
print(C)
|
Output
The 3x3 matrix:
[,1] [,2] [,3]
[1,] 1 2 3
[2,] 4 5 6
[3,] 7 8 9
The 1x3 matrix:
[,1] [,2] [,3]
[1,] 10 11 12
After concatenation of a row:
[,1] [,2] [,3...
Concatenation of a column:
The concatenation of a column to a matrix is done using cbind().
R
A = matrix(
c(1, 2, 3, 4, 5, 6, 7, 8, 9),
nrow = 3,
ncol = 3,
byrow = TRUE
)
cat("The 3x3 matrix:\n")
print(A)
B = matrix(
c(10, 11, 12),
nrow = 3,
ncol = 1,
byrow = TRUE
)
cat("The 3x1 matrix:\n")
print(B)
C = cbind(A, B)
cat("After concatenation of a column:\n")
print(C)
|
Output
The 3x3 matrix:
[,1] [,2] [,3]
[1,] 1 2 3
[2,] 4 5 6
[3,] 7 8 9
The 3x1 matrix:
[,1]
[1,] 10
[2,] 11
[3,] 12
After concatenation of a column:
[,1] [,2] ...
Dimension inconsistency: Note that you have to make sure the consistency of dimensions between the matrix before you do this matrix concatenation.
R
A = matrix(
c(1, 2, 3, 4, 5, 6, 7, 8, 9),
nrow = 3,
ncol = 3,
byrow = TRUE
)
cat("The 3x3 matrix:\n")
print(A)
B = matrix(
c(10, 11, 12),
nrow = 1,
ncol = 3,
)
cat("The 1x3 matrix:\n")
print(B)
C = cbind(A, B)
cat("After concatenation of a column:\n")
print(C)
|
Output:
The 3x3 matrix:
[, 1] [, 2] [, 3]
[1, ] 1 2 3
[2, ] 4 5 6
[3, ] 7 8 9
The 1x3 matrix:
[, 1] [, 2] [, 3]
[1, ] 10 11 12
Error in cbind(A, B) : number of rows of matrices must match (see arg 2)
Adding Rows and Columns in a R-Matrix
To add a row in R-matrix you can use rbind() function and to add a column to R-matrix you can use cbind() function.
Adding Row
Let’s see below example on how to add row in R-matrix?
Example:
R
number <- matrix(
c(1, 2, 3, 4, 5, 6, 7, 8, 9),
nrow = 3,
ncol = 3,
byrow = TRUE
)
cat("Before inserting a new row:\n")
print(number)
new_row <- c(10, 11, 12)
A <- rbind(number[1, ], new_row, number[-1, ])
cat("\nAfter inserting a new row:\n")
print(number)
|
Output
Before inserting a new row:
[,1] [,2] [,3]
[1,] 1 2 3
[2,] 4 5 6
[3,] 7 8 9
After inserting a new row:
[,1] [,2] [,3]
[1,] 1 2 3
[2,] 4 5 6
[3,]...
Adding Column
Let’s see below example on how to add column in R-matrix?
R
number <- matrix(
c(1, 2, 3, 4, 5, 6, 7, 8, 9),
nrow = 3,
ncol = 3,
byrow = TRUE
)
cat("Before adding a new column:\n")
print(number)
new_column <- c(10, 11, 12)
number <- cbind(number, new_column)
cat("\nAfter adding a new column:\n")
print(number)
|
Output
Before adding a new column:
[,1] [,2] [,3]
[1,] 1 2 3
[2,] 4 5 6
[3,] 7 8 9
After adding a new column:
new_column
[1,] 1 2 3 10
[2,] 4 5 6 1...
Deleting Rows and Columns of a R-Matrix
To delete a row or a column, first of all, you need to access that row or column and then insert a negative sign before that row or column. It indicates that you had to delete that row or column.
Row deletion:
R
A = matrix(
c(1, 2, 3, 4, 5, 6, 7, 8, 9),
nrow = 3,
ncol = 3,
byrow = TRUE
)
cat("Before deleting the 2nd row\n")
print(A)
A = A[-2, ]
cat("After deleted the 2nd row\n")
print(A)
|
Output
Before deleting the 2nd row
[,1] [,2] [,3]
[1,] 1 2 3
[2,] 4 5 6
[3,] 7 8 9
After deleted the 2nd row
[,1] [,2] [,3]
[1,] 1 2 3
[2,] 7 8 9
Column deletion:
R
A = matrix(
c(1, 2, 3, 4, 5, 6, 7, 8, 9),
nrow = 3,
ncol = 3,
byrow = TRUE
)
cat("Before deleting the 2nd column\n")
print(A)
A = A[, -2]
cat("After deleted the 2nd column\n")
print(A)
|
Output
Before deleting the 2nd column
[,1] [,2] [,3]
[1,] 1 2 3
[2,] 4 5 6
[3,] 7 8 9
After deleted the 2nd column
[,1] [,2]
[1,] 1 3
[2,] 4 6
[3,] 7 9
We have discussed the about R-matrices and their basic operations like adding new rows and columns, deleting rows and columns, merging matrices,etc.
Hope this helped you in understanding matrices in R, and you can now comfortably use R-matrices in your projects.
Also Check:
Share your thoughts in the comments
Please Login to comment...