Bootstrapping in R Programming
Last Updated :
16 Dec, 2021
Bootstrapping is a technique used in inferential statistics that work on building random samples of single datasets again and again. Bootstrapping allows calculating measures such as mean, median, mode, confidence intervals, etc. of the sampling.
R – Bootstrapping
Following is the process of bootstrapping in R Programming Language:
- Select the number of bootstrap samples.
- Select the size of each sample.
- For each sample, if the size of the sample is less than the chosen sample, then select a random observation from the dataset and add it to the sample.
- Measure the statistic on the sample.
- Measure the mean of all calculated sample values.
Methods of Bootstrapping
There are 2 methods of bootstrapping:
- Residual Resampling: This method is also called as model-based resampling. This method assumes that model is correct and errors are independent and distributed identically. After each resampling, variables are redefined and new variables are used to measure the new dependent variables.
- Bootstrap Pairs: In this method, dependent and independent variables are used together as pairs for sampling.
Types of Confidence Intervals in Bootstrapping
Confidence Interval (CI) is a type of computational value calculated on sample data in statistics. It produces a range of values or an interval where the true value lies for sure. There are 5 types of confidence intervals in bootstrapping as follows:
- Basic: It is also known as Reverse Percentile Interval and is generated using quantiles of bootstrap data distribution. Mathematically,
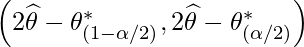
where,
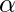 represents confidence interval, mostly
represents confidence interval, mostly 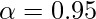
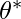 represents bootstrapped coefficients
represents bootstrapped coefficients
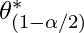 represents
represents 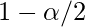 percentile of bootstrapped coefficients
percentile of bootstrapped coefficients
- Normal: Normal CI is mathematically given as,
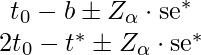
where,
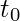 represents a value from dataset t
represents a value from dataset t
b is the bias of bootstrap estimate i.e.,
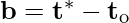
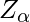 represents
represents 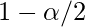 quantile of bootstrap distribution
quantile of bootstrap distribution
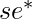 represents standard error of
represents standard error of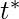
- Stud: In studentized CI, data is normalized with center at 0 and standard deviation 1 correcting the skew of distribution.
- Perc – Percentile CI is similar to basic CI but with different formula,
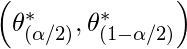
- BCa: This method adjusts for both bias and skewness but can be unstable when outliers are extreme. Mathematically,
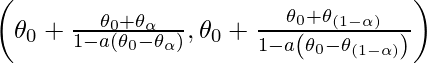
The syntax to perform bootstrapping in R programming is as follows:
Syntax: boot(data, statistic, R)
Parameters:
- data represents dataset
- statistic represents statistic functions to be performed on dataset
- R represents number of samples
To learn about more optional arguments of boot() function, use below command:
help("boot")
Example:
R
install.packages("boot")
library(boot)
bootFunc <- function(data, i){
df <- data[i, ]
c(cor(df[, 2], df[, 3]),
median(df[, 2]),
mean(df[, 1])
)
}
b <- boot(mtcars, bootFunc, R = 100)
print(b)
boot.ci(b, index = 1)
|
Output:
ORDINARY NONPARAMETRIC BOOTSTRAP
Call:
boot(data = mtcars, statistic = bootFunc, R = 100)
Bootstrap Statistics :
original bias std. error
t1* 0.9020329 -0.002195625 0.02104139
t2* 6.0000000 0.340000000 0.85540468
t3* 20.0906250 -0.110812500 0.96052824
BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS
Based on 100 bootstrap replicates
CALL :
boot.ci(boot.out = b, index = 1)
Intervals :
Level Normal Basic
95% ( 0.8592, 0.9375 ) ( 0.8612, 0.9507 )
Level Percentile BCa
95% ( 0.8534, 0.9429 ) ( 0.8279, 0.9280 )
Calculations and Intervals on Original Scale
Some basic intervals may be unstable
Some percentile intervals may be unstable
Warning : BCa Intervals used Extreme Quantiles
Some BCa intervals may be unstable
Warning messages:
1: In boot.ci(b, index = 1) :
bootstrap variances needed for studentized intervals
2: In norm.inter(t, adj.alpha) :
extreme order statistics used as endpoints
Share your thoughts in the comments
Please Login to comment...