Maximum number of parallelograms that can be made using the given length of line segments
Last Updated :
08 May, 2023
Given N line segments where the length of the ith line segment is 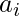 . The task is to find the maximum number of parallelograms can be made with those line segments if each line segment is used at most in one parallelogram.
. The task is to find the maximum number of parallelograms can be made with those line segments if each line segment is used at most in one parallelogram.
Examples:
Input: arr[] = {1, 2, 1, 2}
Output: 1
Only one parallelogram can be made with sides 1, 2, 1, 2
Input: arr[] = {1, 3, 5, 7, 1, 3, 5, 7, 1, 3, 5, 7}
Output: 2
Approach: Make a frequency array of the length of line segments. Then the answer will be the total number of parallelograms that can be made using 4 similar sides + parallelograms that can be made using 2 similar sides. As a parallelogram must have equal opposite sides.
C++
#include <bits/stdc++.h>
using namespace std;
void convert(int n, int a[])
{
int z = a[0];
for (int i = 1; i < n; i++) {
if (a[i] > z)
z = a[i];
}
z = z + 1;
int ff[z] = { 0 };
for (int i = 0; i < n; i++) {
ff[a[i]] += 1;
}
int cc = 0;
for (int i = 0; i < z; i++) {
cc += int(ff[i] / 4);
ff[i] = ff[i] % 4;
}
int vv = 0;
for (int i = 0; i < z; i++) {
if (ff[i] >= 2)
vv += 1;
}
cc += int(vv / 2);
cout << (cc);
}
int main()
{
int n = 4;
int a[] = { 1, 2, 1, 2 };
convert(n, a);
}
|
Java
import java.util.*;
class GFG
{
static void convert(int n, int a[])
{
int z = a[0];
for (int i = 1; i < n; i++)
{
if (a[i] > z)
z = a[i];
}
z = z + 1;
int ff[] = new int[z];
for (int i = 0; i < n; i++)
{
ff[a[i]] += 1;
}
int cc = 0;
for (int i = 0; i < z; i++)
{
cc += (ff[i] / 4);
ff[i] = ff[i] % 4;
}
int vv = 0;
for (int i = 0; i < z; i++)
{
if (ff[i] >= 2)
vv += 1;
}
cc += (vv / 2);
System.out.println(cc);
}
public static void main(String[] args)
{
int n = 4;
int a[] = { 1, 2, 1, 2 };
convert(n, a);
}
}
|
Python
def convert(n, a):
z = max(a)+1
ff =[0]*z
for i in range(n):
ff[a[i]]+= 1
cc = 0
for i in range(z):
cc+= ff[i]//4
ff[i]= ff[i]% 4
vv = 0
for i in range(z):
if(ff[i]>= 2):
vv+= 1
cc+= vv//2
print(cc)
n = 4
a =[1, 2, 1, 2]
convert(n, a)
|
C#
using System;
class GFG
{
static void convert(int n, int []a)
{
int z = a[0];
for (int i = 1; i < n; i++)
{
if (a[i] > z)
z = a[i];
}
z = z + 1;
int []ff = new int[z];
for (int i = 0; i < n; i++)
{
ff[a[i]] += 1;
}
int cc = 0;
for (int i = 0; i < z; i++)
{
cc += (ff[i] / 4);
ff[i] = ff[i] % 4;
}
int vv = 0;
for (int i = 0; i < z; i++)
{
if (ff[i] >= 2)
vv += 1;
}
cc += (vv / 2);
Console.WriteLine(cc);
}
static public void Main ()
{
int n = 4;
int []a = { 1, 2, 1, 2 };
convert(n, a);
}
}
|
Javascript
<script>
function convert(n, a)
{
let z = a[0];
for (let i = 1; i < n; i++)
{
if (a[i] > z)
z = a[i];
}
z = z + 1;
let ff = new Array(z);
ff.fill(0);
for (let i = 0; i < n; i++)
{
ff[a[i]] += 1;
}
let cc = 0;
for (let i = 0; i < z; i++)
{
cc += parseInt(ff[i] / 4, 10);
ff[i] = ff[i] % 4;
}
let vv = 0;
for (let i = 0; i < z; i++)
{
if (ff[i] >= 2)
vv += 1;
}
cc += parseInt(vv / 2, 10);
document.write(cc);
}
let n = 4;
let a = [ 1, 2, 1, 2 ];
convert(n, a);
</script>
|
Time Complexity: O(n)
Space Complexity: O(n)
Share your thoughts in the comments
Please Login to comment...