Python – Binomial Distribution

Binomial distribution is a probability distribution that summarises the likelihood that a variable will take one of two independent values under a given set of parameters. The distribution is obtained by performing a number of Bernoulli trials. A Bernoulli trial is assumed to meet each of these criteria :

• There must be only 2 possible outcomes.
• Each outcome has a fixed probability of occurring. A success has the probability of p, and a failure has the probability of 1 – p.
• Each trial is completely independent of all others.

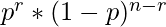
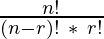
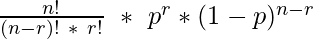
The binomial random variable represents the number of successes(r) in n successive independent trials of a Bernoulli experiment. Probability of achieving r success and n-r failure is : The number of ways we can achieve r successes is :  Hence, the probability mass function(pmf), which is the total probability of achieving r success and n-r failure is : An example illustrating the distribution : Consider a random experiment of tossing a biased coin 6 times where the probability of getting a head is 0.6. If ‘getting a head’ is considered as ‘success’ then, the binomial distribution table will contain the probability of r successes for each possible value of r.

r	0	1	2	3	4	5	6
P(r)	0.004096	0.036864	0.138240	0.276480	0.311040	0.186624	0.046656

This distribution has a mean equal to np and a variance of np(1-p).  Using Python to obtain the distribution : Now, we will use Python to analyse the distribution(using SciPy) and plot the graph(using Matplotlib). Modules required :

• SciPy: SciPy is an Open Source Python library, used in mathematics, engineering, scientific and technical computing. Installation :

  pip install scipy
  

• Matplotlib: Matplotlib is a comprehensive Python library for plotting static and interactive graphs and visualisations. Installation :

  pip install matplotlib
  

The scipy.stats module contains various functions for statistical calculations and tests. The stats() function of the scipy.stats.binom module can be used to calculate a binomial distribution using the values of n and p.

Syntax : scipy.stats.binom.stats(n, p)

It returns a tuple containing the mean and variance of the distribution in that order. scipy.stats.binom.pmf() function is used to obtain the probability mass function for a certain value of r, n and p. We can obtain the distribution by passing all possible values of r(0 to n).

Syntax : scipy.stats.binom.pmf(r, n, p)

Calculating distribution table : Approach :

• Define n and p.
• Define a list of values of r from 0 to n.
• Get mean and variance.
• For each r, calculate the pmf and store in a list.

Code :

from scipy.stats import binom
# setting the values
# of n and p
n = 6
p = 0.6
# defining the list of r values
r_values = list(range(n + 1))
# obtaining the mean and variance
mean, var = binom.stats(n, p)
# list of pmf values
dist = [binom.pmf(r, n, p) for r in r_values ]
# printing the table
print("r\tp(r)")
for i in range(n + 1):
    print(str(r_values[i]) + "\t" + str(dist[i]))
# printing mean and variance
print("mean = "+str(mean))
print("variance = "+str(var))

Output :

r    p(r)
0    0.004096000000000002
1    0.03686400000000005
2    0.13824000000000003
3    0.2764800000000001
4    0.31104
5    0.18662400000000007
6    0.04665599999999999
mean = 3.5999999999999996
variance = 1.44

Code: Plotting the graph using matplotlib.pyplot.bar() function to plot vertical bars.

from scipy.stats import binom
import matplotlib.pyplot as plt
# setting the values
# of n and p
n = 6
p = 0.6
# defining list of r values
r_values = list(range(n + 1))
# list of pmf values
dist = [binom.pmf(r, n, p) for r in r_values ]
# plotting the graph
plt.bar(r_values, dist)
plt.show()

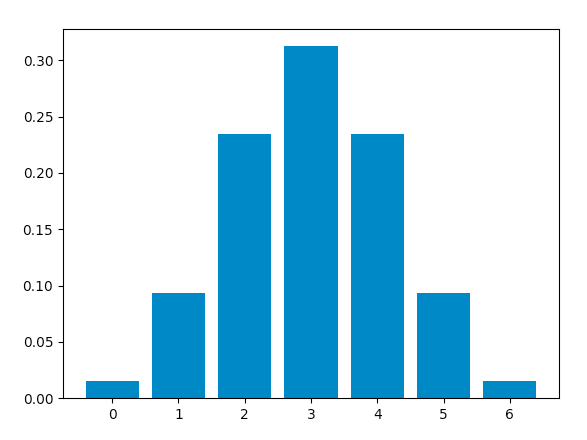
Output : When success and failure are equally likely, the binomial distribution is a normal distribution. Hence, changing the value of p to 0.5, we obtain this graph, which is identical to a normal distribution plot :