Computer Arithmetic | Set – 2

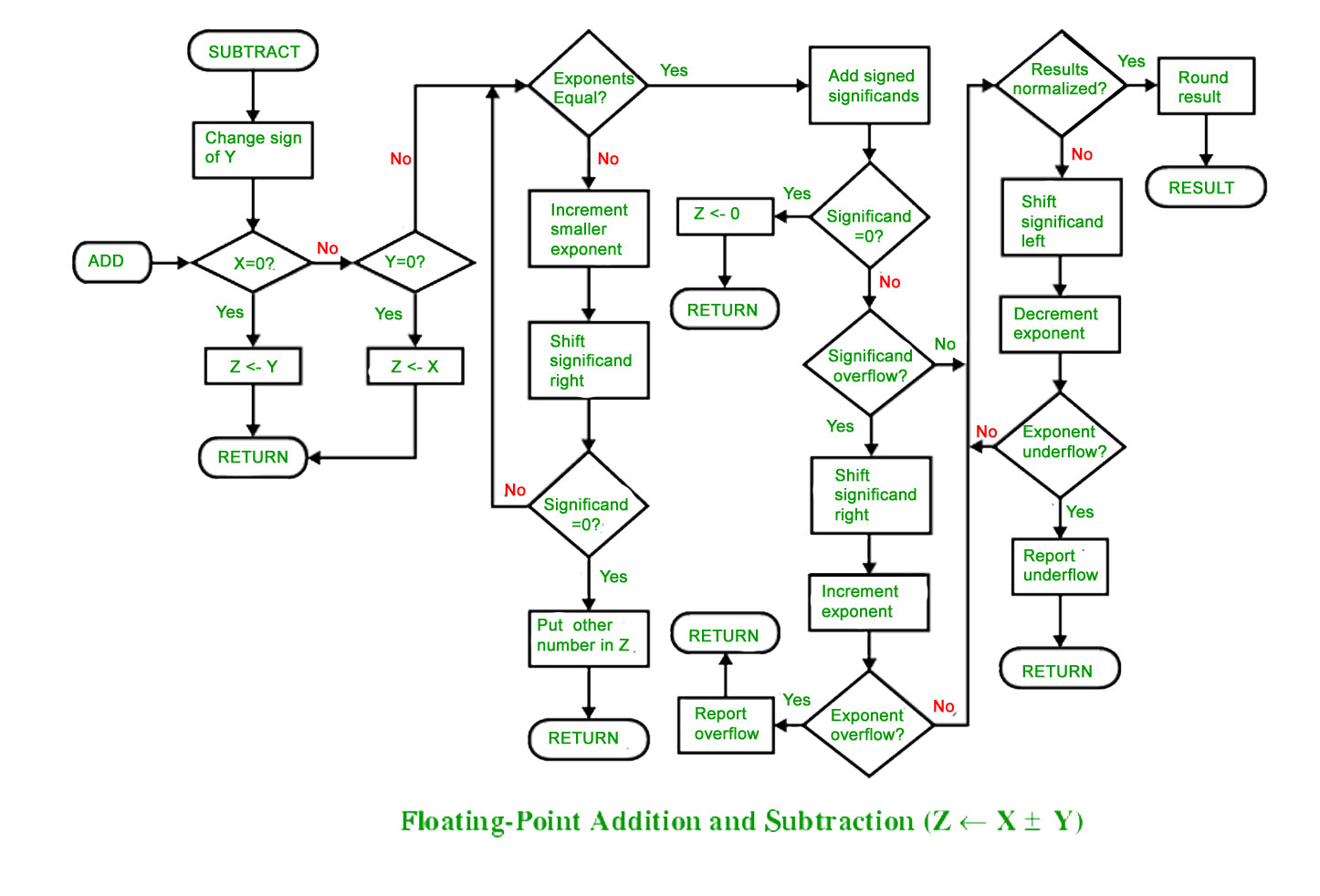
FLOATING POINT ADDITION AND SUBTRACTION 
 

• FLOATING POINT ADDITION

To understand floating point addition, first we see addition of real numbers in decimal as same logic is applied in both cases.

For example, we have to add 1.1 * 10³ and 50.

We cannot add these numbers directly. First, we need to align the exponent and then, we can add significant.

After aligning exponent, we get 50 = 0.05 * 10³

Now adding significant, 0.05 + 1.1 = 1.15

So, finally we get (1.1 * 10³ + 50) = 1.15 * 10³

Here, notice that we shifted 50 and made it 0.05 to add these numbers.

Now let us take example of floating point number addition

We follow these steps to add two numbers: 

1. Align the significant

2. Add the significant 

3. Normalize the result

Let the two numbers be 

x = 9.75 
y = 0.5625

Converting them into 32-bit floating point representation,

9.75’s representation in 32-bit format = 0 10000010 00111000000000000000000 

0.5625’s representation in 32-bit format = 0 01111110 00100000000000000000000

Now we get the difference of exponents to know how much shifting is required. 

(10000010 – 01111110)2 = (4)10

Now, we shift the mantissa of lesser number right side by 4 units.

Mantissa of 0.5625 = 1.00100000000000000000000

(note that 1 before decimal point is understood in 32-bit representation)

Shifting right by 4 units, we get 0.00010010000000000000000 

Mantissa of 9.75 = 1. 00111000000000000000000

Adding mantissa of both

0. 00010010000000000000000

+ 1. 00111000000000000000000

————————————————-

1. 01001010000000000000000

In final answer, we take exponent of bigger number

So, final answer consist of :

Sign bit = 0 

Exponent of bigger number = 10000010

Mantissa = 01001010000000000000000 

32 bit representation of answer = x + y = 0 10000010 01001010000000000000000

• FLOATING POINT SUBTRACTION

Subtraction is similar to addition with some differences like we subtract mantissa unlike addition and in sign bit we put the sign of greater number.

Let the two numbers be 

x = 9.75 
y = – 0.5625

Converting them into 32-bit floating point representation

9.75’s representation in 32-bit format = 0 10000010 00111000000000000000000

– 0.5625’s representation in 32-bit format = 1 01111110 00100000000000000000000

Now, we find the difference of exponents to know how much shifting is required.

(10000010 – 01111110)2 = (4)10 
Now, we shift the mantissa of lesser number right side by 4 units.

Mantissa of – 0.5625 = 1.00100000000000000000000

(note that 1 before decimal point is understood in 32-bit representation)

Shifting right by 4 units, 0.00010010000000000000000 

Mantissa of 9.75= 1. 00111000000000000000000

Subtracting mantissa of both

0. 00010010000000000000000

– 1. 00111000000000000000000

————————————————

1. 00100110000000000000000

Sign bit of bigger number = 0

So, finally the answer = x – y = 0 10000010 00100110000000000000000 

This article has been contributed by Anuj Batham. 

Please write comments if you find anything incorrect, or you want to share more information about the topic discussed above