Non-Restoring Division For Unsigned Integer

In earlier post Restoring Division learned about restoring division. Now, here performing Non-Restoring division, it is less complex than the restoring one because simpler operation are involved i.e. addition and subtraction, also no restoring step is performed. In the method, rely on the sign bit of the register which initially contain zero named as A.

Here is the flow chart given below. 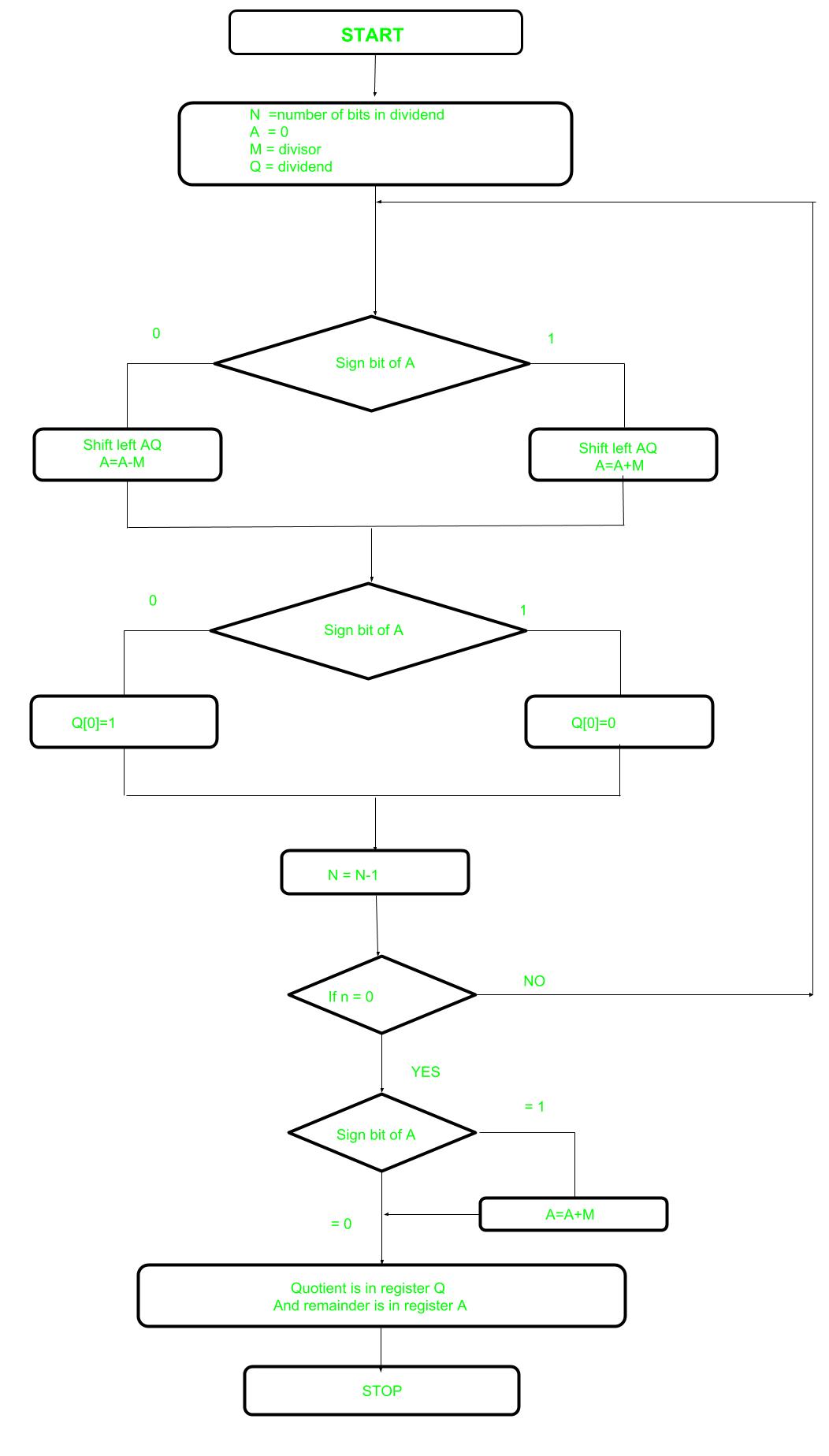Let’s pick the step involved:

• Step-1: First the registers are initialized with corresponding values (Q = Dividend, M = Divisor, A = 0, n = number of bits in dividend)
• Step-2: Check the sign bit of register A
• Step-3: If it is 1 shift left content of AQ and perform A = A+M, otherwise shift left AQ and perform A = A-M (means add 2’s complement of M to A and store it to A)
• Step-4: Again the sign bit of register A
• Step-5: If sign bit is 1 Q[0] become 0 otherwise Q[0] become 1 (Q[0] means least significant bit of register Q)
• Step-6: Decrements value of N by 1
• Step-7: If N is not equal to zero go to Step 2 otherwise go to next step
• Step-8: If sign bit of A is 1 then perform A = A+M
• Step-9: Register Q contains quotient and A contains remainder.

My Personal Notes arrow_drop_up

Save