Overflow in Arithmetic Addition in Binary Number System
Last Updated :
12 Dec, 2022
In Computer Architecture 2’s Complement format is widely used. The discussion of overflow here mainly will be with respect to 2’s Complement representation for signed Integer.
N-bit 2’s Complement representation for signed Integer can represent numbers from 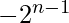 to
to 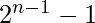
4 Bit can represent numbers from ( -8 to 7 )
5 Bit can represent numbers from ( -16 to 15 ) in 2’s Complimentary System.
Overflow Occurs with respect to addition when 2 N-bit 2’s Complement Numbers are added and the answer is too large to fit into that N-bit Group.
A computer has N-Bit Fixed registers. Addition of two N-Bit Number will result in a max N+1 Bit number. That Extra Bit is stored in the carry Flag. But Carry does not always indicate overflow.

Adding 7 + 1 in 4-Bit must be equal to 8. But 8 cannot be represented with 4 bit 2’s complement number as it is out of range. Two Positive numbers were added and the answer we got is negative (-8). Here Carry is also 0. It is normally left to the programmer to detect overflow and deal with this situation.
Overflow Detection –
Overflow occurs when:
- Two negative numbers are added and an answer comes positive or
- Two positive numbers are added and an answer comes as negative.
Let us understand more in-depth. Consider the below scenarios,
- If x & y are +ve numbers then x+y > max(x,y)
- if x & y are -ve numbers then x+y < min(x,y)
- If x is +ve and y is -ve then y< x+y < x
Considering the above scenarios we can also say that – If we add two operands of same sign and get result of opposite sign, overflow occurs.
So overflow can be detected by checking Most Significant Bit(MSB) of two operands and answer. But Instead of using a 3-bit Comparator, Overflow can also be detected using 2 Bit Comparator just by checking Carry-in(C-in) and Carry-Out(C-out) from MSB’s. Consider the N-Bit Addition of 2’s Complement number.
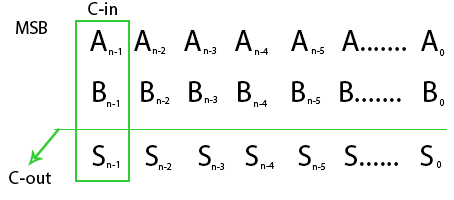
Overflow Occurs when C-in 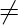 C-out. The above expression for overflow can be explained below Analysis.
C-out. The above expression for overflow can be explained below Analysis.
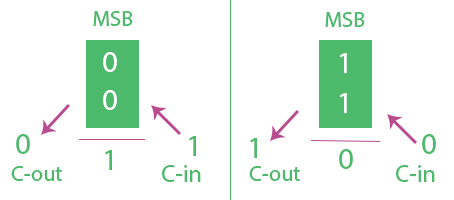
- In first Figure the MSB of two numbers are 0 which means they are positive. Here if C-in is 1 we get answer’s MSB as 1 means answer is negative (Overflow) and C-out as 0. C-in
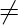 C-out hence overflow.
C-out hence overflow. - In second Figure the MSB of two numbers are 1 which means they are negative. Here if C-in is 0 we get answer MSB as 0 means answer is positive(Overflow) and C-out as 1. C-in
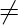 C-out hence overflow.
C-out hence overflow.
Hence, from above discussion we can also conclude that – If carry for MSB(c-in) and carry from MSB(c-out) is different ( considering first figure 1 and 0 respectively) then overflow occurs. Else there is no overflow.
Readers can also try out other combinations of c-in(carry for MSB) c-out(carry from MSB) and MSB’s to check overflow. So Carry-in and Carry-out at MSB’s are enough to detect Overflow.

The above XOR Gate can be used to detect overflow.
Share your thoughts in the comments
Please Login to comment...