Class 11 NCERT Solutions – Chapter 5 Complex Numbers And Quadratic Equations – Miscellaneous Exercise on Chapter 5 | Set 2
Last Updated :
01 Apr, 2021
Question 11. If a + ib = 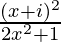 , prove that a2 + b2 =
, prove that a2 + b2 = 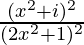
Solution:
Given:
a + ib = 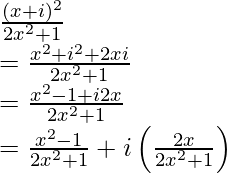
On comparing the real and imaginary parts, we have
a = 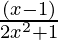 and b =
and b = 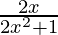
Therefore,
a2 + b2 = 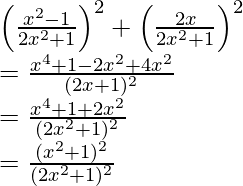
Hence, proved,
a2 + b2 = 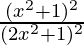
Question 12. Let z1 = 2 – i, z2 = -2 + i. Find
(i) 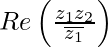
(ii) 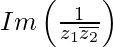
Solution:
(i) Given:
z1 = 2 – i, z2 = -2 + i
(i) z1z2 = (2 – i)(-2 + i) = -4 + 2i + 2i – i2 = -4 + 4i – (-1) = -3 + 4i
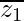 = 2 + i
= 2 + i
Therefore,
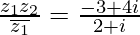
On multiplying numerator and denominator by (2 – i), we get
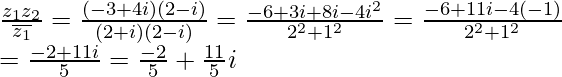
On comparing the real parts, we have
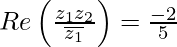
(ii) 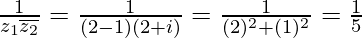
On comparing the imaginary part, we get
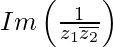 = 0
= 0
Question 13. Find the modulus and argument of the complex number 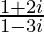
Solution:
Let, z = 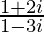 , then
, then
z = 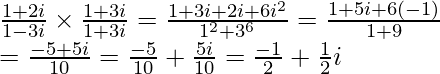
Let z = r cosθ + ir sinθ
So,
r cosθ = 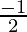 and r sinθ =
and r sinθ = 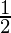
On squaring and adding, we get
r2(cos2θ + sin2θ) = 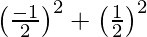
r2 = ![Rendered by QuickLaTeX.com \frac{1}{4}+\frac{1}{4}=\frac{1}{2}\ \ \ \ \ \ [Conventionally,\ r>0]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-c863ca509abcc2270befd0956d32109d_l3.png)
r = 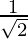
Now,
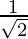 cosθ =
cosθ = 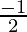 and
and 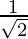 sinθ =
sinθ = 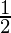
= cosθ = 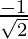 and sinθ =
and sinθ = 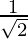
Therefore,
θ = 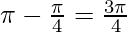 [As θ lies in the II quadrant]
[As θ lies in the II quadrant]
Question 14. Find the real numbers x and y if (x – iy) (3 + 5i) is the conjugate of – 6 – 24i.
Solution:
Let us assume z = (x – iy) (3 + 5i)
z = 3x + xi – 3yi – 5yi2 = 3x + 5xi – 3yi + 5y = (3x + 5y) + i(5x – 3y)
Therefore,
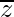 =(3x + 5y) – i(5x – 3y)
=(3x + 5y) – i(5x – 3y)
Also given, 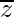 = -6 – 24i
= -6 – 24i
And,
(3x + 5y) – i(5x – 3y) = -6 -24i
After equating real and imaginary parts, we get
3x + 5y = -6 …… (i)
5x – 3y = 24 …… (ii)
After doing (i) x 3 + (ii) x 5, we have
(9x + 15y) + (25x – 15y) = -18 + 120
34x = 102
x = 102/34 = 3
Putting the value of x in equation (i), we get
3(3) + 5y = -6
5y = -6 – 9 = -15
y = -3
Therefore, the values of x and y are 3 and –3 respectively.
Question 15. Find the modulus of 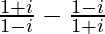
Solution:
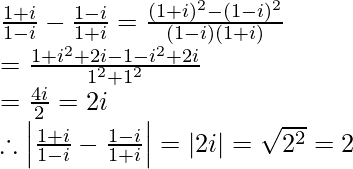
Question 16. If (x + iy)3 = u + iv, then show that 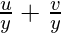 = 4(x2 – y2)
= 4(x2 – y2)
Solution:
(x + iy)3 = u + iv
x3 + (iy)3 + 3 × x × iy(x + iy) = u + iv
x3 + i3y3 + 3x2yi + 3xy2 = u + iv
x3 – iy3 + 3x2yi – 3xy2 = u + iv
(x3 – 3xy2) + i(3x2y – y3) = u + iv
On equating real and imaginary parts, we get
u = x3 – 3xy2, v = 3x2y – y3
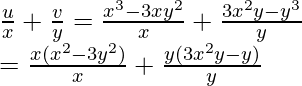
= x2 – 3y2 + 3x2 – y2
= 4x2 – 4y2
= 4(x2 – y2)
Hence proved
Question 17. If α and β are different complex numbers with |β| = 1, then find 
Solution:
Assume α = a + ib and β = x + iy
Given: |β| = 1
So, 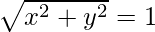
= x2 + y2 = 1 ….(1)
![Rendered by QuickLaTeX.com \left|\frac{\beta-\alpha}{1-\overline{\alpha}\beta}\right|=\left|\frac{(x+iy)(a+ib)}{1-(a-ib)(x+iy)}\right|\\ =\left|\frac{(x-a)+i(y-b)}{1-(ax+aiy-ibx+by)}\right|\\ =\left|\frac{(x-a)+i(y-b)}{(1-ax-by)+i(bx-ay)}\right|\\ =\left|\frac{(x-a)+i(y-b)}{(1-ax-by)+i(bx-ay)}\right|\ \ \ \ \ \left[\left|\frac{z_1}{z_2}\right|=\left|\frac{z_1}{z_2}\right|\right]\\ =\frac{\sqrt{(x-a)^2+(y-b)^2}}{\sqrt{(1-ax-by)^2+(bx-ay)^2}}\\ =\frac{\sqrt{x^2+a^2-2ax+y^2+b^2-2by}}{\sqrt{1+a^2x^2+b^2y^2-2ax+2abxy-2by+b^2x^2+a^2y^2-2abxy}}\\ =\frac{\sqrt{(x^2+y^2)+a^2+b^2-2ax-2by}}{\sqrt{1+a^2(x^2+y^2)+b^2(y^2+x^2)-2ax-2by}}\\ =\frac{\sqrt{1+a^2+b^2-2ax-2by}}{\sqrt{1+a^2+b^2-2ax-2by}}\ \ \ \ \ \ \ \ [Using\ (1)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b0916952a90af051fa6ebd4033c0b4f5_l3.png)
= 1
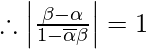
Question 18. Find the number of non-zero integral solutions of the equation |1 – i|x = 2x
Solution:
|1 – i|x = 2t
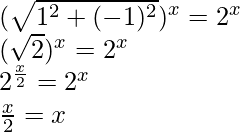
x = 2x
2x – x = 0
Thus, ‘0’ is the only integral solution of the given equation.
Therefore, the number of non-zero integral solutions of the given equation is 0.
Question 19. If (a + ib) (c + id) (e + if) (g + ih) = A + iB, then show that (a2 + b2) (c2 + d2) (e2 + f2) (g2 + h2) = A2 + B2.
Solution:
Given:
(a + ib)(c + id)(e + if)(g + ih) = A + iB
Therefore,
|(a + ib)(c + id)(e + if)(g + ih)| = |A + iB|
= |(a + ib)| × |(c + id)| × |(e + if)| × |(g + ih)| = |A + iB|
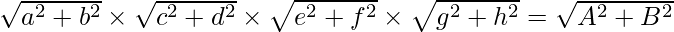
On squaring both sides, we get
(a2 + b2) (c2 + d2) (e2 + f2) (g2 + h2) = A2 + B2
Hence, proved.
Question 20. If, then find the least positive integral value of m. 
Solution:

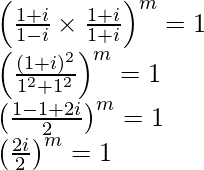
im = 1
Hence, m = 4k, where k is some integer.
Hence, the least positive integer is 1.
Thus, the least positive integral value of m is 4 (= 4 × 1).
Share your thoughts in the comments
Please Login to comment...