Class 11 NCERT Solutions- Chapter 15 Statistics – Exercise 15.2
Last Updated :
25 Feb, 2021
Find the mean and variance for each of the data in Exercise 1 to 5.
Question 1. 6, 7, 10, 12, 13, 4, 8, 12
Solution:
We know,
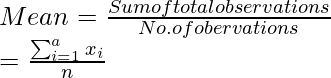
So, 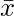 = (6 + 7 + 10 + 12 + 13 + 4 + 8 + 12)/8
= (6 + 7 + 10 + 12 + 13 + 4 + 8 + 12)/8
= 72/8
= 9
| xi |
Deviations from mean
(xi – x’)
| (xi – x’)2 |
| 6 | 6 – 9 = -3 | 9 |
| 7 | 7 – 9 = -2 | 4 |
| 10 | 10 – 9 = 1 | 1 |
| 12 | 12 – 9 = 3 | 9 |
| 13 | 13 – 9 = 4 | 16 |
| 4 | 4 – 9 = – 5 | 25 |
| 8 | 8 – 9 = – 1 | 1 |
| 12 | 12 – 9 = 3 | 9 |
| | | 74 |
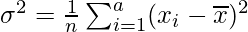
σ2 = (1/8) × 74
= 9.2
Therefore, Mean = 9 and Variance = 9.25
Question 2. First n natural numbers
Solution:
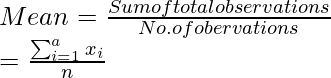
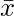 = ((n(n + 1))2)/n
= ((n(n + 1))2)/n
= (n + 1)/2
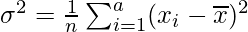
On substituting the value of mean,
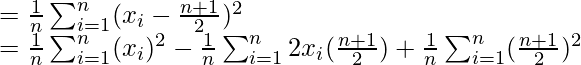 Substituting values of Summation
Substituting values of Summation
![Rendered by QuickLaTeX.com \\ = \frac{1}{n}\frac{n(n+1)(2n+1)}{6}-\frac{n+1}{n}[\frac{n(n+1)}{2}]+\frac{(n+1)^2}{4n}×n](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-14a1132f773d20ea64efe93225d6ac09_l3.png)
On extracting common values, we have,
![Rendered by QuickLaTeX.com = (n+1)[\frac{4n+2-3n-3}{12}] \\ = \frac{(n+1)(n-1)}{12}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-38f66cdd4704db6467c246506cc8ec0b_l3.png)
σ2 = (n2 – 1)/12
Mean = (n + 1)/2 and Variance = (n2 – 1)/12
Question 3. First 10 multiples of 3
Solution:
The required multiples of 3 are 3, 6, 9, 12, 15, 18, 21, 24, 27, 30.
We know,
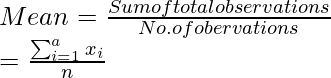
So, 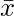 = (3 + 6 + 9 + 12 + 15 + 18 + 21 + 24 + 27 + 30)/10
= (3 + 6 + 9 + 12 + 15 + 18 + 21 + 24 + 27 + 30)/10
= 165/10
= 16.5
| xi |
Deviations from mean
(xi – x’)
| (xi – x’)2 |
| 3 | 3 – 16.5 = -13.5 | 182.25 |
| 6 | 6 – 16.5 = -10.5 | 110.25 |
| 9 | 9 – 16.5 = -7.5 | 56.25 |
| 12 | 12 – 16.5 = -4.5 | 20.25 |
| 15 | 15 – 16.5 = -1.5 | 2.25 |
| 18 | 18 – 16.5 = 1.5 | 2.25 |
| 21 | 21 – 16.5 = – 4.5 | 20.25 |
| 24 | 24 – 16.5 = 7.5 | 56.25 |
| 27 | 27 – 16.5 = 10.5 | 110.25 |
| 30 | 30 – 16.5 = 13.5 | 182.25 |
| | | 742.5 |
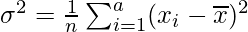
= (1/10) × 742.5
= 74.25
Therefore, Mean = 16.5 and Variance = 74.25
Question 4.
| xi | 6 | 10 | 14 | 18 | 24 | 28 | 30 |
| fi | 2 | 4 | 7 | 12 | 8 | 4 | 3 |
Solution:
| xi | fi | fixi | xi – x’ | (xi – x’)2 | fi(xi – x’)2 |
| 6 | 2 | 12 | 6 – 19 = 13 | 169 | 338 |
| 10 | 4 | 40 | 10-19 = -9 | 81 | 324 |
| 14 | 7 | 98 | 14-19 = -5 | 25 | 175 |
| 18 | 12 | 216 | 18-19 = -1 | 1 | 12 |
| 24 | 8 | 192 | 24-19 = 5 | 25 | 200 |
| 28 | 4 | 112 | 28-19 = 9 | 81 | 324 |
| 30 | 3 | 90 | 30-19 = 11 | 121 | 363 |
| | | | | | 1736 |
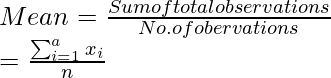
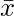 = 760/40
= 760/40
= 19
Also,
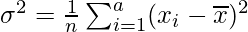
= (1/40) × 1736
= 43.4
Question 5.
| xi | 92 | 93 | 97 | 98 | 102 | 104 | 109 |
| fi | 3 | 2 | 3 | 2 | 6 | 3 | 3 |
Solution:
| xi | fi | fixi | xi – x’ | (xi – x’)2 | fi(xi – x’)2 |
| 92 | 3 | 276 | 92-100 = -8 | 64 | 192 |
| 93 | 2 | 186 | 93-100 = -7 | 49 | 98 |
| 97 | 3 | 291 | 97-100 = -3 | 9 | 27 |
| 98 | 2 | 196 | 98-100 = -2 | 4 | 8 |
| 102 | 6 | 612 | 102-100 = 2 | 4 | 24 |
| 104 | 3 | 312 | 104-100 =4 | 16 | 48 |
| 109 | 3 | 327 | 109-100 = 9 | 81 | 243 |
| | N = 22 | 2200 | | | 640 |
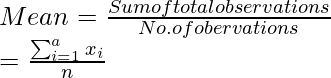
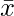 = 2200/22
= 2200/22
= 100
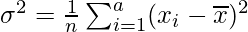
= (1/22) × 640
= 29.09
Therefore, Mean = 100 and Variance = 29.09
Question 6. Find the mean and standard deviation using short-cut method.
| xi | 60 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 |
| fi | 2 | 1 | 12 | 29 | 25 | 12 | 10 | 4 | 5 |
Solution:
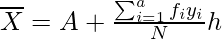
Where A = 64, h = 1
So, 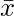 = 64 + ((0/100) × 1)
= 64 + ((0/100) × 1)
= 64 + 0
= 64
Then, variance,
![Rendered by QuickLaTeX.com \sigma^2 = \frac{h^2}{N^2}[N\sum f_iy_i^2 - (\sum f_iy_i)^2]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-5c326f8d99ee2a43dbf9a6ddbc6e6d83_l3.png)
σ2 = (12/1002) [100(286) – 02]
= (1/10000) [28600 – 0]
= 28600/10000
= 2.86
Hence, standard deviation = σ = √2.886
= 1.691
Therefore,
Mean = 64 and Standard Deviation = 1.691
Question 7.
| Classes | 0-30 | 30-60 | 60-90 | 90-120 | 120-150 | 150-180 | 180-210 |
| Frequencies | 2 | 3 | 5 | 10 | 3 | 5 | 2 |
Solution:
| Classes | fi | xi | fixi | (xi – x’) | (xi – x’)2 | fi(xi – x’)2 |
| 0-30 | 2 | 15 | 30 | -92 | 8464 | 16928 |
| 30-60 | 3 | 45 | 135 | -62 | 3844 | 11532 |
| 60-90 | 5 | 75 | 375 | -32 | 1024 | 5120 |
| 90-120 | 10 | 105 | 1050 | -2 | 4 | 40 |
| 120-150 | 3 | 135 | 405 | 28 | 784 | 2352 |
| 150-180 | 5 | 165 | 825 | 58 | 3364 | 16820 |
| 180-210 | 2 | 195 | 390 | 88 | 7744 | 15488 |
| | N = 30 | | 3210 | | | 68280 |
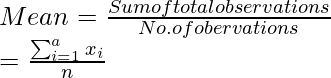
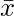 = 3210/30
= 3210/30
= 107
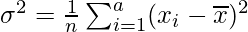
= (1/30) × 68280
= 2276
Therefore, Mean = 107 and Variance = 2276
Question 8.
| Classes | 0-10 | 10-20 | 20-30 | 30-40 | 40-50 |
| Frequencies | 5 | 8 | 15 | 16 | 6 |
Solution:
| Classes | fi | xi | fixi | (xi-x’) | (xi-x’)2 | fi(xi-x’)2 |
| 0-10 | 5 | 5 | 25 | -22 | 484 | 2420 |
| 10-20 | 8 | 15 | 120 | -12 | 144 | 1152 |
| 20-30 | 15 | 25 | 375 | -2 | 4 | 60 |
| 30-40 | 16 | 35 | 560 | 8 | 64 | 1024 |
| 40-50 | 6 | 45 | 270 | 18 | 324 | 1944 |
| | N = 50 | | 1350 | | | 6600 |
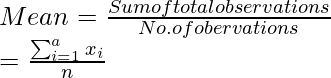
 = 1350/50
= 1350/50
= 27
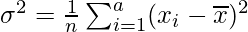
= (1/50) × 6600
= 132
Therefore, Mean = 27 and Variance = 132
Question 9. Find the mean, variance and standard deviation using short-cut method
| Heights in cms | 70-75 | 75-80 | 80-85 | 85-90 | 90-95 | 95-100 | 100-105 | 105-110 | 110-115 |
| Frequencies | 3 | 4 | 7 | 7 | 15 | 9 | 6 | 6 | 3 |
Solution:
| Height | fi | Xi | Yi = (Xi-A)/h | Yi2 | fiyi | fiyi2 |
| 70-75 | 2 | 72.5 | -4 | 19 | -12 | 48 |
| 75-80 | 1 | 77.5 | -3 | 9 | -12 | 36 |
| 80-85 | 12 | 82.5 | -2 | 4 | -14 | 28 |
| 85-90 | 29 | 87.5 | -1 | 1 | -7 | 7 |
| 90-95 | 25 | 92.5 | 0 | 0 | 0 | 0 |
| 95-100 | 12 | 97.5 | 1 | 1 | 9 | 9 |
| 100-105 | 10 | 102.5 | 2 | 4 | 12 | 24 |
| 105-110 | 4 | 107.5 | 3 | 9 | 18 | 54 |
| 110-115 | 5 | 112.5 | 4 | 16 | 12 | 48 |
| 115-120 | N = 60 | | | | 6 | 254 |
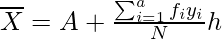
Where, A = 92.5, h = 5
So, 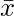 = 92.5 + ((6/60) × 5)
= 92.5 + ((6/60) × 5)
= 92.5 + 0.5
= 92.5 + 0.5
= 93
Then, Variance,
![Rendered by QuickLaTeX.com \sigma^2 = \frac{h^2}{N^2}[N\sum f_iy_i^2 - (\sum f_iy_i)^2]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-5c326f8d99ee2a43dbf9a6ddbc6e6d83_l3.png)
Standard deviation = σ = √105.583
= 10.275
Question 10. The diameters of circles (in mm) drawn in a design are given below:
| Diameters | 33-36 | 37-40 | 41-44 | 45-48 | 49-52 |
| No. of circles | 15 | 17 | 21 | 22 | 25 |
Calculate the standard deviation and mean diameter of the circles.
[Hint first make the data continuous by making the classes as 32.5-36.5, 36.5-40.5, 40.5-44.5, 44.5 – 48.5, 48.5 – 52.5 and then proceed.]
Solution:
| Height | fi | xi | Yi = (Xi-A)/h | Yi2 | fiyi | fiyi2 |
|---|
| 32.5-36.5 | 15 | 34.5 | -2 | 4 | -30 | 60 |
| 36.5-40.5 | 17 | 38.5 | -1 | 1 | -17 | 17 |
| 40.5-44.5 | 21 | 42.5 | 0 | 0 | 0 | 0 |
| 44.5-48.5 | 22 | 46.5 | 1 | 1 | 22 | 22 |
| 48.5-52.5 | 25 | 50.5 | 2 | 4 | 50 | 100 |
| | N=100 | | | | 25 | 199 |
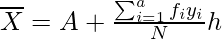
Where, A = 42.5, h = 4
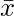 = 42.5 + (25/100) × 4
= 42.5 + (25/100) × 4
= 42.5 + 1
= 43.5
Then, Variance,
![Rendered by QuickLaTeX.com \sigma^2 = \frac{h^2}{N^2}[N\sum f_iy_i^2 - (\sum f_iy_i)^2]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-5c326f8d99ee2a43dbf9a6ddbc6e6d83_l3.png)
σ2 = (42/1002)[100(199) – 252]
On solving, we get,
= (1/625) [19900 – 625]
= 19275/625
= 771/25
= 30.84
Hence, standard deviation = σ = √30.84
= 5.553
Share your thoughts in the comments
Please Login to comment...