Question 1. The relation f is defined by f(x) = {x2, 0 ≤ x ≤ 3 3x, 3 ≤ x ≤ 10}
The relation g is defined by g(x) = {x2, 0 ≤ x ≤ 2 3x, 2 ≤ x ≤ 10}.
Show that f is a function and g is not a function.
Solution:
The given relation f is defined as:
f(x) = {x2, 0≤x≤3
3x, 3≤x≤10}
It is given that, for the condition 0 ≤ x < 3,
Solution of f(x) = x2 and
For the condition 3 < x ≤ 10, solution of f(x) = 3x.
Now for the value of x = 3, solution of f(x) by putting the value of x, f(x) = 32 = 9
or, f(x) = 3 × 3 = 9.
That means, at x = 3, f(x) = 9 [Single image]
So that, for 0 ≤ x ≤ 10, the images of f(x) are unique.
Therefore, the given relation is a function.
Now,
In the given relation g is defined as:
g(x) = {x2, 0≤x≤2
3x, 2≤x≤10}
It is seen that, in case of both the condition, for x = 2,
The value of g(x), by putting the value of x, g(x) = 22= 4 and g(x) = 3 × 2 = 6.
So that, element 2 of the domain of the relation g corresponds to two different images i.e., 4 and 6.
Therefore, this relation is not a function.
Question 2. If f(x) = x2, find 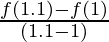 .
.
Solution:
Given:
f(x) = x2 .
Hence, by putting the condition of f(x) in f(1.1) and f(1),
we can find the result of the given equation
((f(1.1) – f(1))/(1.1 – 1)) = (((1.1)2 – (1)2)/(1.1 – 1))
= ((1.21-1)/(0.1))
= (0.21/0.1)
= 2.1
Question 3. Find the domain of the function f(x) = 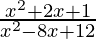 ((x2+2x+1)/(x2-8x+12)).
((x2+2x+1)/(x2-8x+12)).
Solution:
Given function:
f(x) = ((x2+2x+1)/(x2-8x+12))
= (((x2+2x+1)/((x-6)(x-2)))
It is clearly notified that, the function f is defined for all real numbers except
at x = 6 and x = 2 as the denominator becomes zero otherwise.
Question 4. Find the domain and the range of the real function f defined by f(x) = √(x – 1).
Solution:
Given real function:
f(x) = √(x – 1).
Clearly it is notified, √(x – 1) is defined for (x – 1) ≥ 0.
Hence, the function f(x) = √(x – 1) is defined for x ≥ 1.
So that, the domain of f is the set of all real numbers greater than or equal to 1.
Domain of f = [1, ∞).
Now,
According to the condition, x ≥ 1 ⇒ (x – 1) ≥ 0 ⇒ √(x – 1) ≥ 0
That’s why, the range of f is the set of all real numbers greater than or equal to 0.
Range of f = [0, ∞).
Therefore, the domain of f is R – {2, 6}.
Question 5. Find the domain and the range of the real function f defined by f (x) = |x – 1|.
Solution:
Given real function: f(x) = |x – 1|
Clearly it is notified that, the function |x – 1| is defined for all real numbers.
Hence, Domain of f = R
Also, according to the condition , for x ∈ R, |x – 1| assumes all real numbers.
So that, the range of f is the set of all non-negative real numbers.
Question 6. Let f={(x, 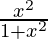 )}: x ∈ R} be a function from R into R. Determine the range of f.
)}: x ∈ R} be a function from R into R. Determine the range of f.
Solution:
Given function:
f = {(x, x2/1+x2): x ∈ R}
Substituting values and determining the images, we have
={(0,0), (±0.5, 1/5), (±1, 1/2), (±1.5, 9/13), (±2, 4/5), (3, 9/10), (4,16/17), …..}
From the above equation, the range of f is the set of all second elements.
It can be notified that all these elements are greater than or equal to 0 but less than 1.
[As the denominator is greater than the numerator.]
Or, We know that, for x ∈ R,
x2≥ 0
Then,
x2 + 1 ≥ x2
1 ≥ (x2 / (x2 + 1))
Therefore, the range of f = [0, 1)
Question 7. Let f, g: R → R be defined, respectively by f(x) = x + 1, g(x) = 2x – 3. Find f + g, f – g, and f/g.
Solution:
According to the question, let us assume, the functions f, g: R → R is defined as
given conditions f(x) = x + 1, g(x) = 2x – 3.
Now,
We find that (f + g) (x) = f(x) + g(x) = (x + 1) + (2x – 3) = 3x – 2
So that, (f + g) (x) = 3x – 2
Now, we find that, (f – g) (x) = f(x) – g(x) = (x + 1) – (2x – 3) = x + 1 – 2x + 3 = – x + 4
So that, (f – g) (x) = -x + 4
(f/g(x)) = f(x)/g(x), g(x) ≠ 0, x ∈ R
(f/g(x)) = x + 1/ 2x – 3, 2x – 3 ≠ 0
So that, (f/g(x)) = x + 1/ 2x – 3, x ≠ 3/2.
Question 8. Let f = {(1, 1), (2, 3), (0, –1), (–1, –3)} be a function from Z to Z defined by f(x) = ax + b, for some integers a, b. Determine a, b.
Solution:
Given the values, f = {(1, 1), (2, 3), (0, –1), (–1, –3)}
And according to the question, the function is defined as, f(x) = ax + b
For (1, 1) ∈ f
We have, f(1) = 1
So, a × 1 + b = 1
a + b = 1 …. (i)
And for (0, -1) ∈ f
We have f(0) = -1
a × 0 + b = -1
So, b = -1
Now, On substituting b = –1 in (i), we get
Putting the value here, a + (–1) = 1 ⇒ a = 1 + 1 = 2.
Hereby, the values of a and b are 2 and –1 respectively.
Question 9. Let R be a relation from N to N defined by R = {(a, b): a, b ∈ N and a = b2}. Are the following true?
(i) (a, a) ∈ R, for all a ∈ N
(ii) (a, b) ∈ R, implies (b, a) ∈ R
(iii) (a, b) ∈ R, (b, c) ∈ R implies (a, c) ∈ R.
Justify your answer in each case.
Solution:
According to the question, Given relation R = {(a, b): a, b ∈ N and a = b2}
(i) It can be notified that 2 ∈ N; however, 2 ≠ 22 = 4.
Hence, it is notified that the statement “(a, a) ∈ R, for all a ∈ N” is not true.
(ii) Its clearly notified that (9, 3) ∈ N because 9, 3 ∈ N and 9 = 32.
Now, it’s clear that 3 ≠ 92 = 81; therefore, (3, 9) ∉ N
Hence, it is notified that the statement “(a, b) ∈ R, implies (b, a) ∈ R” is not true.
(iii) Its clearly notified that (16, 4) ∈ R, (4, 2) ∈ R because 16, 4, 2 ∈ N and 16 = 42 and 4 = 22.
Now, it is clear that 16 ≠ 22 = 4; therefore, (16, 2) ∉ N
Hence, it is notified that the statement “(a, b) ∈ R, (b, c) ∈ R implies (a, c) ∈ R” is not true.
Question 10. Let A = {1, 2, 3, 4}, B = {1, 5, 9, 11, 15, 16} and f = {(1, 5), (2, 9), (3, 1), (4, 5), (2, 11)}. Are the following true?
(i) f is a relation from A to B
(ii) f is a function from A to B.
Justify your answer in each case.
Solution:
Given, A = {1, 2, 3, 4} and B = {1, 5, 9, 11, 15, 16}
So,
A × B = {(1, 1), (1, 5), (1, 9), (1, 11), (1, 15), (1, 16), (2, 1), (2, 5),
(2, 9), (2, 11), (2, 15), (2, 16), (3, 1), (3, 5), (3, 9), (3, 11),
(3, 15), (3, 16), (4, 1), (4, 5), (4, 9), (4, 11), (4, 15), (4, 16)}
Also given in the question that, f = {(1, 5), (2, 9), (3, 1), (4, 5), (2, 11)}
(i) The verified statement is : A relation from a non-empty set A to a non-empty
set B is a subset of the Cartesian product A × B.
It’s clearly notified that f is a subset of A × B.
Hence, it’s clear that f is a relation from A to B.
(ii) From the given condition, as the same first element i.e., 2 corresponds to two
different images (9 and 11), relation f is not a function.
Question 11. Let f be the subset of Z × Z defined by f = {(ab, a + b): a, b ∈ Z}. Is f a function from Z to Z: justify your answer?
Solution:
According to the question, Given relation f is defined as f = {(ab, a + b): a, b ∈ Z}.
Now, we know that a relation f from a set A to a set B is said to be a function
if every element of set A has unique images in set B.
As 2, 6, –2, –6 ∈ Z, (2 × 6, 2 + 6), (–2 × –6, –2 + (–6)) ∈ f
i.e., (12, 8), (12, –8) ∈ f
It’s clearly notified that, the same first element, 12 corresponds
to two different images (8 and –8).
Therefore, the relation f is not a function.
Question 12. Let A = {9, 10, 11, 12, 13} and let f: A → N be defined by f(n) = the highest prime factor of n. Find the range of f.
Solution:
Given, A = {9, 10, 11, 12, 13}
Now, f: A → N is defined as
f(n) = The highest prime factor of n.
So, Prime factor of 9 = 3
Prime factors of 10 = 2, 5
Prime factor of 11 = 11
Prime factors of 12 = 2, 3
Prime factor of 13 = 13
Hence, it can be expressed as:
Here,
f(9) means the highest prime factor of 9 = 3
f(10) means the highest prime factor of 10 = 5
f(11) means the highest prime factor of 11 = 11
f(12) means the highest prime factor of 12 = 3
f(13) means the highest prime factor of 13 = 13
So that, the range of f is the set of all f(n), where n ∈ A.
Therefore,
Range of f = {3, 5, 11, 13}.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...