Pizza Puzzle
Last Updated :
18 Jan, 2023
Problem Statement:
At a restaurant, pizzas can be ordered in boxes of 6, 9, and 20. What is the highest number of Pizzas that cannot be bought with any combination of these boxes?
For Example:

- There exist two types of solutions for such a problem.
- They include mathematical and algorithmic ones.
- The mathematical solution is limited only to the given box values while the algorithmic solution can be applied to any box values.
Mathematical Solution:
- The combination of 6 and 9 will give you all the multiples of 3 (except 3 pizzas).
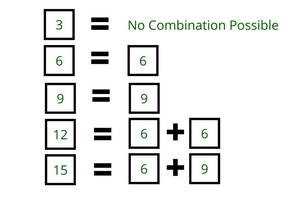
- If a number is not a multiple of 3, then use one box of 20. Calculate the remaining value and check if it is a multiple of 3. For example:
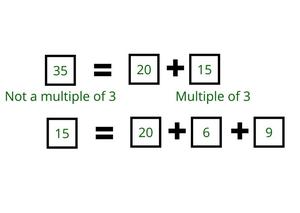
- Therefore, it is possible to buy 35 pizza boxes.
- But it is not possible to buy 28 boxes because after using one box of 20 only 8 boxes are left which is not the multiple of 3.
- Similarly, after using 1 box of 20, if the remaining number is not divisible by 3, then check if another box of 20 can be used.
- For example:
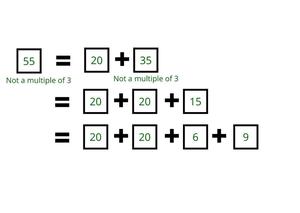
- Repeatedly subtract 20 from a given number until get a number divisible by 3.
- This approach always works, because any number when divided by 3 gives a remainder of 0, 1 or 2.
- For example, 15 is divisible by 3, so get a remainder of 0 on dividing 15 by 3.
- Now, if take any number which is not a multiple of 3 and add it to 15 repeatedly and divide the addition result by 3.
- The remainder will be taken as an output sequence as 0, 1, 2 0, 1, 2 01, 2 or 0, 2, 1 0, 2, 1 0, 2, 1.
- From the above approach, it looks like any number of pizzas>= 40 can be bought but there is 1 number above 20 which cannot be achieved by any combination of 20, 9, and 6.
- After using a maximum of 2 boxes of 20, the remaining value must be divisible by 3. As seen above, number 3 cannot be achieved by any combination of 20, 9, and 6.
- The highest number of pizzas that can’t be bought= 20+ 20+ 3= 43.
Algorithm:
- The smallest box is 6.
- If achieve 6 consecutive numbers, then get all further numbers by simply adding one more box of 6.
- For example:
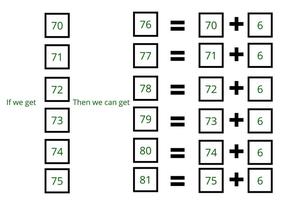
- So the target is to found those 6 consecutive numbers.
- Let’s make combinations to achieve a number of pizza boxes in increasing order.
- On observing the pattern 6 consecutive numbers will be taken from 44 to 49.
- Therefore, it can be achieved any number of boxes greater than 49 with the help of one more box of 6.
- So, the highest number of boxes that cannot be obtained by any combination of 20, 9, and 6 are present before 44 i.e. 43. This is the required answer.
Share your thoughts in the comments
Please Login to comment...