Find the centroid of a non-self-intersecting closed Polygon
Last Updated :
01 Mar, 2022
Given N vertices of the polygon, the task is to find the centroid of the polygon
Examples:
Input: ar = {{0, 0}, {0, 8}, {8, 8}, {8, 0}}
Output: {Cx, Cy} = {4, 4}
Input: ar = {{1, 2}, {3, -4}, {6, -7}}
Output: {Cx, Cy} = {3.33, -3}
Approach:
The centroid of a non-self-intersecting closed polygon defined by n vertices (x0, y0), (x1, y1), …, (xn-1, yn-1) is the point (Cx, Cy), where:
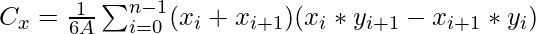
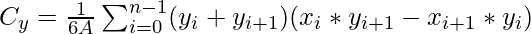
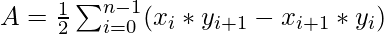
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
pair<double, double> find_Centroid(vector<pair<double, double> >& v)
{
pair<double, double> ans = { 0, 0 };
int n = v.size();
double signedArea = 0;
for (int i = 0; i < v.size(); i++) {
double x0 = v[i].first, y0 = v[i].second;
double x1 = v[(i + 1) % n].first, y1 =
v[(i + 1) % n].second;
double A = (x0 * y1) - (x1 * y0);
signedArea += A;
ans.first += (x0 + x1) * A;
ans.second += (y0 + y1) * A;
}
signedArea *= 0.5;
ans.first = (ans.first) / (6 * signedArea);
ans.second = (ans.second) / (6 * signedArea);
return ans;
}
int main()
{
vector<pair<double, double> > vp = { { 1, 2 },
{ 3, -4 },
{ 6, -7 } };
pair<double, double> ans = find_Centroid(vp);
cout << setprecision(12) << ans.first << " "
<< ans.second << '\n';
return 0;
}
|
Java
class GFG
{
static double[] find_Centroid(double v[][])
{
double []ans = new double[2];
int n = v.length;
double signedArea = 0;
for (int i = 0; i < n; i++)
{
double x0 = v[i][0], y0 = v[i][1];
double x1 = v[(i + 1) % n][0], y1 = v[(i + 1) % n][1];
double A = (x0 * y1) - (x1 * y0);
signedArea += A;
ans[0] += (x0 + x1) * A;
ans[1] += (y0 + y1) * A;
}
signedArea *= 0.5;
ans[0] = (ans[0]) / (6 * signedArea);
ans[1]= (ans[1]) / (6 * signedArea);
return ans;
}
public static void main (String[] args)
{
double vp[][] = { { 1, 2 },
{ 3, -4 },
{ 6, -7 } };
double []ans = find_Centroid(vp);
System.out.println(ans[0] + " " + ans[1]);
}
}
|
Python3
def find_Centroid(v):
ans = [0, 0]
n = len(v)
signedArea = 0
for i in range(len(v)):
x0 = v[i][0]
y0 = v[i][1]
x1 = v[(i + 1) % n][0]
y1 =v[(i + 1) % n][1]
A = (x0 * y1) - (x1 * y0)
signedArea += A
ans[0] += (x0 + x1) * A
ans[1] += (y0 + y1) * A
signedArea *= 0.5
ans[0] = (ans[0]) / (6 * signedArea)
ans[1] = (ans[1]) / (6 * signedArea)
return ans
vp = [ [ 1, 2 ],
[ 3, -4 ],
[ 6, -7 ] ]
ans = find_Centroid(vp)
print(round(ans[0], 12), ans[1])
|
C#
using System;
class GFG
{
static double[] find_Centroid(double [,]v)
{
double []ans = new double[2];
int n = v.GetLength(0);
double signedArea = 0;
for (int i = 0; i < n; i++)
{
double x0 = v[i, 0], y0 = v[i, 1];
double x1 = v[(i + 1) % n, 0],
y1 = v[(i + 1) % n, 1];
double A = (x0 * y1) - (x1 * y0);
signedArea += A;
ans[0] += (x0 + x1) * A;
ans[1] += (y0 + y1) * A;
}
signedArea *= 0.5;
ans[0] = (ans[0]) / (6 * signedArea);
ans[1]= (ans[1]) / (6 * signedArea);
return ans;
}
public static void Main (String[] args)
{
double [,]vp = { { 1, 2 },
{ 3, -4 },
{ 6, -7 } };
double []ans = find_Centroid(vp);
Console.WriteLine(ans[0] + " " + ans[1]);
}
}
|
Javascript
<script>
function find_Centroid(v)
{
let ans = new Array(2);
ans.fill(0);
let n = v.length;
let signedArea = 0;
for (let i = 0; i < n; i++)
{
let x0 = v[i][0], y0 = v[i][1];
let x1 = v[(i + 1) % n][0], y1 = v[(i + 1) % n][1];
let A = (x0 * y1) - (x1 * y0);
signedArea += A;
ans[0] += (x0 + x1) * A;
ans[1] += (y0 + y1) * A;
}
signedArea *= 0.5;
ans[0] = (ans[0]) / (6 * signedArea);
ans[1]= (ans[1]) / (6 * signedArea);
return ans;
}
let vp = [ [ 1, 2 ],
[ 3, -4 ],
[ 6, -7 ] ];
let ans = find_Centroid(vp);
document.write(ans[0].toFixed(11) + " " + ans[1]);
</script>
|
Time Complexity: O(n)
Auxiliary Space: O(1)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...