Covariance and Correlation in R Programming

Covariance and Correlation are terms used in statistics to measure relationships between two random variables. Both of these terms measure linear dependency between a pair of random variables or bivariate data. 

In this article, we are going to discuss cov(), cor() and cov2cor() functions in R which use covariance and correlation methods of statistics and probability theory.

Covariance in R Programming Language

In R programming, covariance can be measured using cov() function. Covariance is a statistical term used to measures the direction of the linear relationship between the data vectors. Mathematically, 

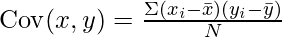
where, 

x represents the x data vector 
y represents the y data vector 
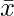represents mean of x data vector 
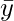represents mean of y data vector 
N represents total observations

Covariance Syntax in R

Syntax: cov(x, y, method)

where, 

• x and y represents the data vectors
• method defines the type of method to be used to compute covariance. Default is “pearson”.

Example:

R

# Data vectors
x <- c(1, 3, 5, 10)

y <- c(2, 4, 6, 20)

# Print covariance using different methods
print(cov(x, y))
print(cov(x, y, method = "pearson"))
print(cov(x, y, method = "kendall"))
print(cov(x, y, method = "spearman"))

Output:

[1] 30.66667
[1] 30.66667
[1] 12
[1] 1.666667

Correlation in R Programming Language

cor() function in R programming measures the correlation coefficient value. Correlation is a relationship term in statistics that uses the covariance method to measure how strong the vectors are related. Mathematically,

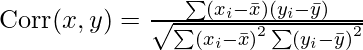
where, 

x represents the x data vector 
y represents the y data vector 
[Tex]\bar{x}  [/Tex]represents mean of x data vector 
[Tex]\bar{y}  [/Tex]represents mean of y data vector

Correlation in R

Syntax: cor(x, y, method)

where, 

• x and y represents the data vectors
• method defines the type of method to be used to compute covariance. Default is “pearson”.

Example:

R

# Data vectors
x <- c(1, 3, 5, 10)

y <- c(2, 4, 6, 20)

# Print correlation using different methods
print(cor(x, y))

print(cor(x, y, method = "pearson"))
print(cor(x, y, method = "kendall"))
print(cor(x, y, method = "spearman"))

Output:

[1] 0.9724702
[1] 0.9724702
[1] 1
[1] 1

Conversion of Covariance to Correlation in R

cov2cor() function in R programming converts a covariance matrix into corresponding correlation matrix.

Syntax: cov2cor(X)

where, 

• X and y represents the covariance square matrix

Example:

R

# Data vectors
x <- rnorm(2)
y <- rnorm(2)

# Binding into square matrix
mat <- cbind(x, y)

# Defining X as the covariance matrix
X <- cov(mat)

# Print covariance matrix
print(X)

# Print correlation matrix of data
# vector
print(cor(mat))

# Using function cov2cor()
# To convert covariance matrix to
# correlation matrix
print(cov2cor(X))

Output:

           x          y
x  0.0742700 -0.1268199
y -0.1268199  0.2165516

   x  y
x  1 -1
y -1  1

   x  y
x  1 -1
y -1  1