Spearman Correlation Testing in R Programming
Last Updated :
11 May, 2023
The strength of the association between two variables is known as the correlation test. For instance, if one is interested to know whether there is a relationship between the weights of mothers and daughters, a correlation coefficient can be calculated to answer this question. To know more about correlation please refer Correlation.
Methods for Correlation Analysis
There are mainly two types of correlation:
- Parametric Correlation – Pearson correlation(r) : It measures a linear dependence between two variables (x and y) and is known as a parametric correlation test because it depends on the distribution of the data.
- Non-Parametric Correlation – Kendall(tau) and Spearman(rho): They are rank-based correlation coefficients, known as non-parametric correlation.
Spearman Correlation formula
Spearman Correlation is a non-parametric correlation also known as rank-based correlation coefficient. The formula for calculating Spearman Correlation is as follows: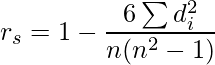
where, rs: Spearman Correlation coefficient di: The difference in the ranks given to the two variables values for each item of the data, n: Total number of observation
Note:
- rs takes a value between -1 (negative association) and 1 (positive association).
- rs = 0 means there is no association.
- If association is monotonically increasing then rs = 1.
- If association is monotonically decreasing then rs = -1.
- It can be used when association is nonlinear.
- It can be applied for ordinal variables.
Implementation in R
R Language provides two methods to calculate the correlation coefficient. By using the functions cor() or cor.test() it can be calculated. It can be noted that cor() computes the correlation coefficient whereas cor.test() computes test for association or correlation between paired samples. It returns both the correlation coefficient and the significance level(or p-value) of the correlation.
Syntax: cor(x, y, method = “spearman”) cor.test(x, y, method = “spearman”) Parameters: x, y: numeric vectors with the same length method: correlation method
Using cor() method
R
x = c(15, 18, 21, 15, 21)
y = c(25, 25, 27, 27, 27)
result = cor(x, y, method = "spearman")
cat("Spearman correlation coefficient is:", result)
|
Output:
Spearman correlation coefficient is: 0.4564355
Using cor.test() method
R
x = c(15, 18, 21, 15, 21)
y = c(25, 25, 27, 27, 27)
result = cor.test(x, y, method = "spearman")
print(result)
|
Output:
Spearman's rank correlation rho
data: x and y
S = 10.871, p-value = 0.4397
alternative hypothesis: true rho is not equal to 0
sample estimates:
rho
0.4564355
In the output above:
- S is the value of the test statistic (S = 10.871)
- p-value is the significance level of the test statistic (p-value = 0.4397).
- alternative hypothesis is a character string describing the alternative hypothesis (true rho is not equal to 0).
- sample estimates is the correlation coefficient. For Spearman correlation coefficient it’s named as rho (Cor.coeff = 0.4564).
Example with Dataset
Download the CSV file here.
R
df = read.csv("Auto.csv")
x = df$mpg
y = df$weight
result = cor(x, y, method ="spearman")
cat("Spearman correlation coefficient is:", result)
res = cor.test(x, y, method = "spearman")
print(res)
|
Output:
Spearman correlation coefficient is: -0.9140708
Spearman's rank correlation rho
data: x and y
S = 8613223, p-value < 2.2e-16
alternative hypothesis: true rho is not equal to 0
sample estimates:
rho
-0.9140708
Share your thoughts in the comments
Please Login to comment...