Class 11 NCERT Solutions- Chapter 10 Straight Lines – Exercise 10.2 | Set 2

Chapter 10 Straight Lines – Exercise 10.2 | Set 1

Question 11. A line perpendicular to the line segment joining the points (1, 0) and (2, 3) divides it in the ratio 1: n. Find the equation of the line.

Solution:

Slope of line segment will be m1 = (y2 – y1)/(x2 – x1)

= (3 – 0)/(2 – 1)

= 3/1

= 3

If two line are perpendicular to each other than slope of line1 X slope of line2 = -1

So, the slope of line will be m2 = (-1/m1)

m2 = -1/3

As we know that the coordinates of a point (p, q) dividing the line 

segment joining the points (x1, y1) and (x2, y2) internally 

In the ratio m : n are:

(p, q) = ((mx2 + nx1)/(m + n), (my2 + ny1)/(m + n))

(p, q) = ((1 × 2 + n × 1)/(1 + n), (1 × 3 + n × 0)/(1 + n))

p = (2 + n)/(1 + n)

q = 3/(1 + n)

We know that the point (p, q) lies on the line with slope m2,

Equation of line will be y – q = m2(x – p)

y – 3/(1 + n) = (–1/3)(x – (2 + n)/(1 + n))

3((1 + n) y – 3) = (–(1 + n) x + 2 + n)

3(1 + n) y – 9 = – (1 + n) x + 2 + n

(1 + n) x + 3(1 + n) y – n – 9 – 2 = 0

(1 + n) x + 3(1 + n) y – n – 11 = 0

So, the equation of the line is (1 + n) x + 3(1 + n) y – n – 11 = 0

Question 12. Find the equation of a line that cuts off equal intercepts on the coordinate axes and passes through the point (2, 3).

Solution:

Given that the line cuts off equal intercepts on the coordinate axes i.e. a = b.

So, the equation of the line intercepts a and b on x-and y-axis, respectively, which is

x/a + y/b = 1

So, x/a + y/a = 1

x + y = a            -(1)

Given point is (2, 3)

2 + 3 = a

a = 5

On substituting the value of ‘a’ in eq(1), we get

x + y = 5

x + y – 5 = 0

So, the equation of the line is x + y – 5 = 0.

Question 13. Find equation of the line passing through the point (2, 2) and cutting off intercepts on the axes whose sum is 9.

Solution:

Equation of the line making intercepts a and b on x-and y-axis, respectively, is 

x/a + y/b = 1          -(1)

Given that sum of intercepts = 9

a + b = 9

b = 9 – a

On substituting the value of b in the eq(1), we get

x/a + y/(9 – a) = 1

Given that the line passes through the point (2, 2),

So, 2/a + 2/(9 – a) = 1

[2(9 – a) + 2a] / a(9 – a) = 1

[18 – 2a + 2a] / a(9 – a) = 1

18/a(9 – a) = 1

18 = a (9 – a)

18 = 9a – a²

a² – 9a + 18 = 0

By using factorization method for quadratic equation solving, we get

a2 – 3a – 6a + 18 = 0

a (a – 3) – 6 (a – 3) = 0

(a – 3) (a – 6) = 0

a = 3 or a = 6

Let us substitute in eq(1),

Case 1 (a = 3):

Then b = 9 – 3 = 6

x/3 + y/6 = 1

2x + y = 6

2x + y – 6 = 0

Case 2 (a = 6):

Then b = 9 – 6 = 3

x/6 + y/3 = 1

x + 2y = 6

x + 2y – 6 = 0

So, the equation of the line is 2x + y – 6 = 0 or x + 2y – 6 = 0

Question 14. Find equation of the line through the point (0, 2) making an angle 2π/3 with the positive x-axis. Also, find the equation of line parallel to it and crossing the y-axis at a distance of 2 units below the origin.

Solution:

Given that

Point (0, 2) and θ = 2π/3

slope (m)= tan θ

m = tan (2π/3) = -√3

Now, the equation of line passing through point(p,q) with slope m will be:

y – q = m (x – p)

y – 2 = -√3 (x – 0)

y – 2 = -√3 x

√3 x + y – 2 = 0

Now we need to find equation of line parallel to above obtained equation 

crosses the y-axis at a distance of 2 units below the origin.

So, the point = (0, -2) and for parallel line slope will be same that is m = -√3

From point slope form equation,

y – (–2) = –√3 (x – 0)

y + 2 = -√3 x

√3 x + y + 2 = 0

So, the equation of line is √3 x + y – 2 = 0 and the line parallel to it is √3 x + y + 2 = 0.

Question 15. The perpendicular from the origin to a line meets it at the point (–2, 9), find the equation of the line.

Solution:

Perpendicular line will pass through point (0,0) and (-2,9) as per given question,

Then slope of perpendicular line will be m1 = (y2 – y1)/(x2 – x1)

= (9 – 0)/(–2 – 0)

= –9/2

As we know that two non-vertical lines are perpendicular to each 

other if their slopes are negative reciprocals of each other.

So, we need to find equation of line let say it AB.

Slope of line AB will be m = (–1/m1) = –1/(–9/2) = 2/9

As perpendicular line and line intersecting at (–2, 9) that means (–2, 9) lies on the line AB

By using Slope Point Form of line, we get

y – y1 = m (x – x1)

y – 9 = (2/9) (x – (–2))

9(y – 9) = 2(x + 2)

9y – 81 = 2x + 4

2x + 4 – 9y + 81 = 0

2x – 9y + 85 = 0

So, the equation of line is 2x – 9y + 85 = 0.

Question 16. The length L (in centimeter) of a copper rod is a linear function of its Celsius temperature C. In an experiment, if L = 124.942 when C = 20 and L= 125.134 when C = 110, express L in terms of C.

Solution:

Let us considered ‘L’ along X-axis and ‘C’ along Y-axis, 

So, we have two points (124.942, 20) and (125.134, 110) in XY-plane.

As we know that the equation of the line passing through the points (x1, y1) and (x2, y2) is given by

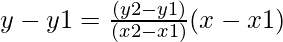
0.192(C-20) = 90(L – 124.942)

 L can be express in Terms of C in following manner

L = (0.192 × (C – 20)/90) + 124.942

Question 17. The owner of a milk store finds that he can sell 980 liters of milk each week at Rs. 14/liter and 1220 liters of milk each week at Rs. 16/liter. Assuming a linear relationship between the selling price and demand, how many liters could he sell weekly at Rs. 17/liter?

Solution:

Let us considered the relationship between selling price and demand is linear.

So, the selling price per liter along X-axis and demand along Y-axis, 

We have two points (14, 980) and (16, 1220) in XY-plane

We know that the equation of the line passing through the points (x1, y1) and (x2, y2) is given by

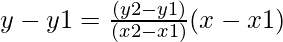
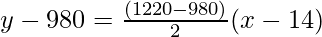
y – 980 = 120 (x – 14)

y = 120 (x – 14) + 980

When x = Rs 17/liter,

y = 120 (17 – 14) + 980

y = 120(3) + 980

y = 360 + 980 = 1340

So, the owner can sell 1340 liters weekly at Rs. 17/liter.

Question 18. P (a, b) is the mid-point of a line segment between axes. Show that equation of the line is x/a + y/b = 2

Solution:

Let us considered AB be a line segment whose midpoint is P (a, b).

So, the coordinates of A is (0, y) and B is (x, 0) 

Mid-Point of AB will be P(a, b) = ((x + 0)/2, (y + 0)/2)

a = x/2 

x = 2a

And

b = y/2 

y = 2b

That means line AB is passing from (0, 2b) and (2a, 0)

We know that the equation of the line passing through the points (x1, y1) and (x2, y2) is given by

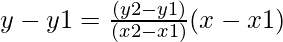
(y – 2b) = ((0 – 2b)/2a) × x

a (y – 2b) = –bx

ay – 2ab = –bx

bx + ay = 2ab

On dividing both the sides with ab, we get

x/a + y/b =2

Question 19. Point R (h, k) divides a line segment between the axes in the ratio 1: 2. Find the equation of the line.

Solution:

Let us consider, PQ be the line segment such that r (h, k) divides it in the ratio 1: 2.

So the coordinates of P and Q be (0, y) and (x, 0) respectively.

We know that the coordinates of a point dividing the line segment

 joins the points (x1, y1) and (x2, y2) internally in the ratio m: n is

(h, k) = ((mx2 + nx1)/(m + n), (my2 + ny1)/(m + n))

(h, k) = ((1 × 0 + 2 × x)/(1 + 2), (1 × y + 2 × 0)/(1 + 2))

h = 2x/3 and k = y/3

x = 3h/2 and y = 3k

So, P = (0, 3k) and Q = (3h/2, 0)

We know that the equation of the line passing through the points (x1, y1) and (x2, y2) is given by

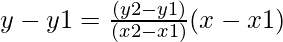
y – 3k = ((0 – 3k)/(3h/2))x

3h(y – 3k) = –6kx

3hy – 9hk = –6kx

6kx + 3hy = 9hk

On dividing both the sides by 9hk, we get,

2x/3h + y/3k = 1

So, the equation of the line is given by 2x/3h + y/3k = 1

Question 20. By using the concept of equation of a line, prove that the three points (3, 0), (– 2, – 2), and (8, 2) are collinear.

Solution:

Prove that the given three points (3, 0), (– 2, – 2) and (8, 2) are collinear, 

So, we have to also prove that the line passing through the points 

(3, 0) and (– 2, – 2) also passes through the point (8, 2).

The equation of the line passing through the points (x1, y1) and (x2, y2) is given by

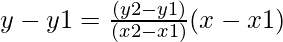
y – 0 = ((–2 – 0)/(–2 – 3)) × (x – 3)

–5y = –2 (x – 3)

–5y = –2x + 6

2x – 5y = 6

Checking whether (8,2) is on line 2x – 5y = 6 or not,

LHS = 2x – 5y = 2(8) – 5(2)

= 16 – 10

= 6

= RHS

So, the line passing through the points (3, 0) and (– 2, – 2) 

also passes through the point (8, 2).

Hence, proved that the points (3, 0), (– 2, – 2) and (8, 2) are collinear,