In each of the Exercises 1 to 6, find the coordinates of the foci and the vertices, the eccentricity and the length of the latus rectum of the hyperbolas.
Question 1.  = 1
= 1
Solution:
Comparing the given equation with 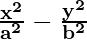 = 1,
= 1,
we conclude that transverse axis is along x-axis.
a2 = 16 and b2 = 9
a = ±4 and b = ±3
Foci:
Foci = (c, 0) and (-c, 0)
c = √(a2+b2)
c = √(16+9)
c = √25
c = 5
So the foci is (5, 0) and (-5, 0)
Vertices:
Vertices = (a, 0) and (-a, 0)
So the vertices is (4, 0) and (-4, 0)
Eccentricity:
Eccentricity = c/a = 5/4
Length of the latus rectum:
Length of the latus rectum = 2b2/a
= 2×9/4
= 9/2
Question 2. 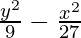 = 1
= 1
Solution:
Comparing the given equation with  = 1,
= 1,
we conclude that transverse axis is along y-axis.
a2 = 9 and b2 = 27
a = ±3 and b = ±3√3
Foci:
Foci = (0, c) and (0, -c)
c = √(a2 + b2)
c = √(9 + 27)
c = √36
c = 6
So the foci is (0,6) and (0,-6)
Vertices:
Vertices = (0,a) and (0,-a)
So the vertices is (0,3) and (0,-3)
Eccentricity:
Eccentricity = c/a
= 6/3
= 2
Length of the latus rectum:
Length of the latus rectum = 2b2/a
= 2×27/3
= 18
Question 3. 9y2 – 4x2 = 36
Solution:
9y2 – 4x2 = 36
On dividing LHS and RHS by 36,
9y2/36 – 4x2/36 = 36/36
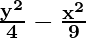 = 1
= 1
Comparing the given equation with  = 1,
= 1,
we conclude that transverse axis is along y-axis.
a2 = 4 and b2 = 9
a = ±2 and b = ±3
Foci:
Foci = (0, c) and (0, -c)
c = √(a2 + b2)
c = √(4 + 9)
c = √13
So the foci is (0, √13) and (0, -√13)
Vertices:
Vertices = (0, a) and (0, -a)
So the vertices is (0, 2) and (0, -2)
Eccentricity:
Eccentricity = c/a
= √13/2
Length of the latus rectum:
Length of the latus rectum = 2b2/a
= 2×9/2
= 9
Question 4. 16x2 – 9y2 = 576
Solution:
16x2 – 9y2 = 576
On dividing LHS and RHS by 576,
16x2/576 – 9y2/576 = 576/576
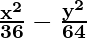 = 1
= 1
Comparing the given equation with 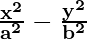 = 1,
= 1,
we conclude that transverse axis is along x-axis.
a2 = 36 and b2 = 64
a = ±6 and b = ±8
Foci:
Foci = (c,0) and (-c,0)
c = √(a2 + b2)
c = √(36 + 64)
c = √100
c = 10
So the foci is (10, 0) and (-10, 0)
Vertices:
Vertices = (a, 0) and (-a, 0)
So the vertices is (6, 0) and (-6, 0)
Eccentricity:
Eccentricity = c/a
= 10/6 = 5/3
Length of the latus rectum:
Length of the latus rectum = 2b2/a
= 2×64/6
= 64/3
Question 5. 5y2 – 9x2 = 36
Solution:
5y2 – 9x2 = 36
On dividing LHS and RHS by 36,
5y2/36 – 9x2/36 = 36/36
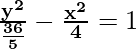
Comparing the given equation with  = 1,
= 1,
we conclude that transverse axis is along y-axis.
a2 = 36/5 and b2 = 4
a = ±6/√5 and b = ±2
Foci:
Foci = (0, c) and (0, -c)
c = √(a2 + b2)
c = √(36/5 + 4)
c = √56/5
c = 2√14/√5
So the foci is (0, 2√14/√5) and (0, -2√14/√5)
Vertices:
Vertices = (0, a) and (0, -a)
So the vertices is (0,6/√5) and (0,-6/√5)
Eccentricity:
Eccentricity = c/a
= (2√14/√5)/6/√5
= √14/3
Length of the latus rectum:
Length of the latus rectum = 2b2/a
= 2×4/(6/√5)
= 4√5/3
Question 6. 49y2 – 16x2 = 784
Solution:
49y2 – 16x2 = 784
On dividing LHS and RHS by 784, we get
49y2/784 – 16x2/784 = 784/784
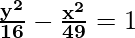
Comparing the given equation with  = 1,
= 1,
we conclude that transverse axis is along y-axis.
a2 = 16 and b2 = 49
a = ±4 and b = ±7
Foci:
Foci = (0, c) and (0, -c)
c = √(a2 + b2)
c = √(16 + 49)
c = √65
So the foci is (0, √65) and (0, -√65)
Vertices:
Vertices = (0, a) and (0, -a)
So the vertices is (0, 4) and (0, -4)
Eccentricity:
Eccentricity = c/a = √65/4
Length of the latus rectum:
Length of the latus rectum = 2b2/a
= 2×49/4
= 49/2
In each of the Exercises 7 to 15, find the equations of the hyperbola satisfying the given conditions.
Question 7. Vertices (± 2, 0), foci (± 3, 0).
Solution:
Since the foci is on x-axis, the equation of the hyperbola is of the form
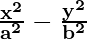 = 1
= 1
As, Vertices (± 2, 0) and foci (±3, 0)
So, a = ±2 and c = ±3
As, c = √(a2 + b2)
b2 = c2 – a2
b2 = 9 – 4
b2 = 5
So, a2 = 4 and b2 = 5
Hence, the equation is
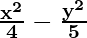 = 1
= 1
Question 8. Vertices (0, ± 5), foci (0, ± 8).
Solution:
Since the foci is on y-axis, the equation of the hyperbola is of the form
 = 1
= 1
As, Vertices (0, ±5) and foci (0, ±8)
So, a = ±5 and c = ±8
As, c = √(a2 + b2)
b2 = c2 – a2
b2 = 64 – 25
b2 = 39
So, a2 = 25 and b2 = 39
Hence, the equation is
 = 1
= 1
Question 9. Vertices (0, ± 3), foci (0, ± 5).
Solution:
Since the foci is on y-axis, the equation of the hyperbola is of the form
 = 1
= 1
As, Vertices (0, ± 3) and foci (0, ± 5)
So, a = ±3 and c = ±5
As, c = √(a2 + b2)
b2 = c2 – a2
b2 = 25 – 9
b2 = 16
So, a2 = 9 and b2 = 16
Hence, the equation is
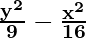 = 1
= 1
Question 10. Foci (± 5, 0), the transverse axis is of length 8.
Solution:
Since the foci is on x-axis, the equation of the hyperbola is of the form
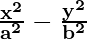 = 1
= 1
As, Foci (±5, 0) ⇒ c = ±5
Since, the length of the transverse axis is 8,
2a = 8
a = 8/2
a = 4
As, c = √(a2 + b2)
b2 = c2 – a2
b2 = 25 – 16
b2 = 9
So, a2 = 16 and b2 = 9
Hence, the equation is
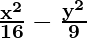 = 1
= 1
Question 11. Foci (0, ±13), the conjugate axis is of length 24.
Solution:
Since the foci is on y-axis, the equation of the hyperbola is of the form
 = 1
= 1
As, Foci (0, ± 13) ⇒ c = ±13
Since, the length of the conjugate axis is 24,
2b = 24
b = 24/2
b = 12
As, c = √(a2 + b2)
a2 = c2 – b2
a2 = 169 – 144
a2 = 25
So, a2 = 25 and b2 = 144
Hence, the equation is
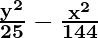 = 1
= 1
Question 12. Foci (± 3√5, 0), the latus rectum is of length 8.
Solution:
Since the foci is on x-axis, the equation of the hyperbola is of the form
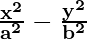 = 1
= 1
As, Foci (±3√5, 0) ⇒ c = ±3√5
Since, the length of latus rectum is 8,
2b2/a = 8
b2 = 8a/2
b2 = 4a -(1)
As, c = √(a2 + b2)
b2 = 45 – a2
4a = 45 – a2
a2 + 4a – 45 = 0
a2 + 9a – 5a – 45 = 0
(a + 9)(a – 5) = 0
a ≠ -9 (a has to be positive due to eq(1))
Hence, a = 5
From eq(1), we get
b2 = 4(5)
b2 = 20
So, a2 = 25 and b2 = 20
Hence, the equation is
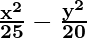 = 1
= 1
Question 13. Foci (± 4, 0), the latus rectum is of length 12.
Solution:
Since the foci is on x-axis, the equation of the hyperbola is of the form
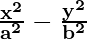 = 1
= 1
As, Foci (±4, 0) ⇒ c=±4
Since, the length of latus rectum is 12,
2b2/a = 12
b2 = 12a/2
b2 = 6a -(1)
As, c = √(a2 + b2)
b2 = 16 – a2
6a = 16 – a2
a2 + 6a – 16 = 0
a2 + 8a – 2a – 16 = 0
(a + 8)(a – 2) = 0
a ≠ -8 (a has to be positive due to eq(1))
Hence, a = 2
From eq(1), we get
b2 = 6(2)
b2 = 12
So, a2 = 4 and b2 = 12
Hence, the equation is
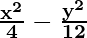 = 1
= 1
Question 14. Vertices (± 7, 0), e = 4/3.
Solution:
Since the vertex is on x-axis, the equation of the hyperbola is of the form
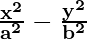 = 1
= 1
As, Vertices (±7, 0) ⇒ a = ±7
As e = 4/3
c/a = 4/3
c = 4a/3
c = 28/3
As, c = √(a2 + b2)
b2 = 784/9 – 49
b2 = 343/9
So, a2 = 49 and b2 = 343/9
Hence, the equation is
x2/49 – y2/(343/9) = 1
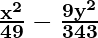 = 1
= 1
Question 15. Foci (0, ±√10), passing through (2, 3).
Solution:
Since the foci is on y-axis, the equation of the hyperbola is of the form
 = 1
= 1
As, Foci (0, ±√10) ⇒ c=±√10
As, c = √(a2 + b2)
b2 = c2 – a2
b2 = 10 – a2 -(1)
As (2, 3) passes through the curve, hence
32/a2 – 22/b2 = 1
9/a2 – 4/b2 = 1
9/a2 – 4/(10 – a2) = 1
9(10 – a2) – 4a2 = a2(10 – a2)
90 – 9a2 – 4a2 = 10a2 – a4
a4 – 23a2 + 90 = 0
a4 – 18a2 – 5a2 + 90 = 0
a2(a2 – 18) – 5(a2 – 18) = 0
(a2 – 18)(a2 – 5) = 0
a2 = 18 or 5
As, a < c in hyperbola
So a2 = 5
And, b2 = 10 – 5 -(From eq(1))
b2 = 5
So, a2 = 5 and b2 = 5
Hence, the equation is 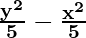 = 1
= 1
Share your thoughts in the comments
Please Login to comment...