In each of the Exercises 1 to 9, find the coordinates of the foci, the vertices, the length of the major axis, the minor axis, the eccentricity, and the length of the latus rectum of the ellipse.
Question 1.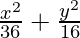 = 1
= 1
Solution:
Since denominator of x2/36 is larger than the denominator of y2/16,
the major axis is along the x-axis.
On comparing the given equation with 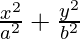 = 1, we get
= 1, we get
a2 = 36 and b2 = 16
⇒ a = ±6 and b = ±4
The Foci:
Foci = (c, 0) and (-c, 0) when (a2 > b2)
c = √(a2 – b2) -(when a2 > b2)
c = √(36 – 16)
c = √20 = 2√5
⇒ (2√5, 0) and (-2√5, 0)
Vertices:
Vertices = (a, 0) and (-a, 0) when (a2 > b2)
⇒ (6, 0) and (-6, 0)
Length of major axis:
Length of major axis = 2a (when a2 > b2)
= 2 × 6
⇒ Length of major axis = 12
Length of minor axis:
Length of minor axis = 2b (when a2 > b2)
= 2 × 4
⇒ Length of minor axis = 8
Eccentricity
Eccentricity = c/a (when a2 > b2)
= 2√5/6
= √5/3
Length of the latus rectum:
Length of the latus rectum = 2b2/a (when a2 > b2)
= 2×16/6
= 16/3
Question 2. 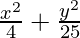 = 1
= 1
Solution:
Since denominator of y2/25 is larger than the denominator of x2/4,
the major axis is along the y-axis.
Comparing the given equation with 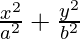 = 1, we get
= 1, we get
a2 = 4 and b2 = 25
⇒ a = ±2 and b = ±5
The Foci:
Foci = (0, c) and (0, -c) when (a2 < b2)
c = √(b2 – a2) -(when a2 < b2)
c = √(25 – 4)
c = √21
⇒ (0, √21) and (0, -√21)
Vertices:
Vertices = (0, b) and (0, -b) when (a2 < b2)
⇒ (0, 5) and (0, -5)
Length of major axis:
Length of major axis = 2b (when a2 < b2)
= 2 × 5
⇒ Length of major axis = 10
Length of minor axis:
Length of minor axis = 2a (when a2 < b2)
=2 × 2
⇒ Length of minor axis = 4
Eccentricity:
Eccentricity = c/b (when a2 < b2)
= √21/5
Length of the latus rectum:
Length of the latus rectum = 2a2/b (when a2 < b2)
= 2×4/5
= 8/5
Question 3. 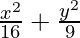 = 1
= 1
Solution:
Since denominator of x2/16 is larger than the denominator of y2/9,
the major axis is along the x-axis.
Comparing the given equation with 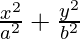 = 1, we get
= 1, we get
a2 = 16 and b2 = 9
⇒ a = ±4 and b = ±3
The Foci:
Foci = (c, 0) and (-c, 0) when (a2 > b2)
c = √(a2 – b2) -(when a2 > b2)
c = √(16 – 9)
c = √7
⇒ (√7, 0) and (-√7, 0).
Vertices:
Vertices = (a, 0) and (-a, 0) when (a2 > b2)
⇒ (4,0) and (-4,0)
Length of major axis:
Length of major axis = 2a (when a2 > b2)
= 2 × 4
⇒ Length of major axis = 8
Length of minor axis:
Length of minor axis = 2b (when a2 > b2)
= 2 × 3
⇒ Length of minor axis = 6
Eccentricity:
Eccentricity = c/a (when a2>b2)
= √7/4
Length of the latus rectum:
Length of the latus rectum = 2b2/a (when a2 > b2)
= 2 × 9/4
= 9/2
Question 4. 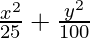 = 1
= 1
Solution:
Since denominator of y2/100 is larger than the denominator of x2/25,
the major axis is along the y-axis.
Comparing the given equation with 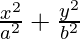 = 1, we get
= 1, we get
a2 = 25 and b2 = 100
⇒ a = ±5 and b = ±10
The Foci:
Foci = (0, c) and (0, -c) when (a2 < b2)
c = √(b2 – a2) -(when a2 < b2)
c = √(100 – 25)
c = √75
c = 5√3
⇒ (0, 5√3) and (0, -5√3)
Vertices:
Vertices = (0, b) and (0, -b) when (a2 < b2)
⇒ (0, 10) and (0, -10)
Length of major axis:
Length of major axis = 2b (when a2 < b2)
= 2 × 10
⇒ Length of major axis = 20
Length of minor axis:
Length of minor axis = 2a (when a2 < b2)
= 2 × 5
⇒ Length of minor axis = 10
Eccentricity:
Eccentricity = c/b (when a2 < b2)
= 5√3/10
= √3/2
Length of the latus rectum:
Length of the latus rectum = 2a2/b (when a2 < b2)
= 2 × 25/10
= 5
Question 5. 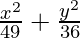 = 1
= 1
Solution:
Since denominator of x2/49 is larger than the denominator of y2/36,
the major axis is along the x-axis.
Comparing the given equation with 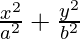 = 1, we get
= 1, we get
a2 = 49 and b2 = 36
⇒ a = ±7 and b = ±6
The Foci:
Foci = (c, 0) and (-c, 0) when (a2 > b2)
c = √(a2 – b2) -(when a2 > b2)
c = √(49 – 36)
c = √13
⇒ (√13, 0) and (-√13, 0).
Vertices:
Vertices = (a, 0) and (-a, 0) when (a2 > b2)
⇒ (7, 0) and (-7, 0)
Length of major axis:
Length of major axis = 2a (when a2 > b2)
= 2 × 7
⇒ Length of major axis = 14
Length of minor axis:
Length of minor axis = 2b (when a2 > b2)
= 2 × 6
⇒ Length of minor axis = 12
Eccentricity:
Eccentricity = c/a (when a2 > b2)
= √13/7
Length of the latus rectum:
Length of the latus rectum = 2b2/a (when a2 > b2)
= 2 × 36/7
= 72/7
Question 6. 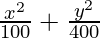 = 1
= 1
Solution:
Since denominator of y2/400 is larger than the denominator of x2/100,
the major axis is along the y-axis.
Comparing the given equation with 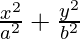 = 1, we get
= 1, we get
a2 = 100 and b2 = 400
⇒ a = ±10 and b = ±20
The Foci:
Foci = (0, c) and (0, -c) when (a2 < b2)
c = √(b2 – a2) -(when a2 < b2)
c = √(400 – 100)
c = √300
c = 10√3
⇒ (0, 10√3) and (0, -10√3)
Vertices:
Vertices = (0, b) and (0, -b) when (a2 < b2)
⇒ (0, 20) and (0, -20)
Length of major axis:
Length of major axis = 2b (when a2 < b2)
= 2 × 20
⇒ Length of major axis = 40
Length of minor axis:
Length of minor axis = 2a (when a2 < b2)
= 2 × 10
⇒ Length of minor axis = 20
Eccentricity:
Eccentricity = c/b (when a2 < b2)
= 10√3/20
= √3/2
Length of the latus rectum:
Length of the latus rectum = 2a2/b (when a2 < b2)
= 2×100/20
= 10
Question 7. 36x2 + 4y2 = 144
Solution:
36x2 + 4y2 = 144
Dividing LHS and RHS by144,
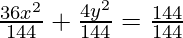
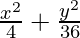 = 1 (Obtained Equation)
= 1 (Obtained Equation)
Since denominator of y2/36 is larger than the denominator of x2/4,
the major axis is along the y-axis.
Comparing the given equation with 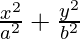 = 1, we get
= 1, we get
a2 = 4 and b2 = 36
⇒ a = ±2 and b = ±6
The Foci:
Foci = (0, c) and (0, -c) when (a2 < b2)
c = √(b2 – a2) -(when a2 < b2)
c = √(36 – 4)
c = √32
c = 4√2
⇒ (0, 4√2) and (0, -4√2)
Vertices:
Vertices = (0, b) and (0, -b) when (a2 < b2)
⇒ (0, 6) and (0, -6)
Length of major axis:
Length of major axis = 2b (when a2<b2)
= 2 × 6
⇒ Length of major axis = 12
Length of minor axis
Length of minor axis = 2a (when a2 < b2)
= 2 × 2
⇒ Length of minor axis = 4
Eccentricity:
Eccentricity = c/b (when a2 < b2)
= 4√2/6
= 2√2/3
Length of the latus rectum:
Length of the latus rectum = 2a2/b (when a2 < b2)
= 2 × 4/6
= 4/3
Question 8. 16x2 + y2 = 16
Solution:
16x2 + y2 = 16
Dividing LHS and RHS by16,
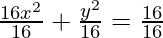
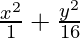 = 1 (Obtained Equation)
= 1 (Obtained Equation)
Since denominator of y2/16 is larger than the denominator of x2/1,
the major axis is along the y-axis.
Comparing the given equation with 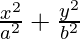 = 1, we get
= 1, we get
a2 = 1 and b2 = 16
⇒ a = ±1 and b = ±4
The Foci:
Foci = (0, c) and (0, -c) when (a2 < b2)
c = √(b2 – a2) -(when a2 < b2)
c = √(16 – 1)
c = √15
⇒ (0, √15) and (0, -√15)
Vertices:
Vertices = (0, b) and (0, -b) when (a2 < b2)
⇒ (0, 4) and (0, -4)
Length of major axis:
Length of major axis = 2b (when a2 < b2)
= 2 × 4
⇒ Length of major axis = 8
Length of minor axis:
Length of minor axis = 2a (when a2 < b2)
=2 × 1
⇒ Length of minor axis = 2
Eccentricity:
Eccentricity = c/b (when a2 < b2)
= √15/4
Length of the latus rectum:
Length of the latus rectum = 2a2/b (when a2 < b2)
= 2 × 1/4
= 1/2
Question 9. 4x2 + 9y2 = 36
Solution:
4x2 + 9y2 = 36
Dividing LHS and RHS by 36,
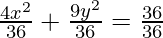
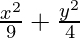 = 1 (Obtained Equation)
= 1 (Obtained Equation)
Since denominator of x2/9 is larger than the denominator of y2/4,
the major axis is along the x-axis.
Comparing the given equation with 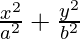 = 1, we get
= 1, we get
a2 = 9 and b2 = 4
⇒ a = ±3 and b = ±2
The Foci:
Foci = (c, 0) and (-c, 0) when (a2 > b2)
c = √(a2 – b2) -(when a2 > b2)
c = √(9 – 4)
c = √5
⇒ (√5, 0) and (-√5, 0).
Vertices
Vertices = (a, 0) and (-a, 0) when (a2 > b2)
⇒ (3, 0) and (-3, 0).
Length of major axis
Length of major axis = 2a (when a2 > b2)
= 2 × 3
⇒ Length of major axis = 6
Length of minor axis
Length of minor axis = 2b (when a2 > b2)
= 2 × 2
⇒ Length of minor axis = 4
Eccentricity
Eccentricity = c/a (when a2 > b2)
= √5/3
Length of the latus rectum
Length of the latus rectum = 2b2/a (when a2 > b2)
= 2 × 4/3
= 8/3
In each of the following Exercises 10 to 20, find the equation for the ellipse that satisfies the given conditions:
Question 10. Vertices (± 5, 0), foci (± 4, 0).
Solution:
Since the vertices are on x-axis, the equation will be of the form
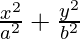 = 1, where a is the semi-major axis. (where a2 > b2)
= 1, where a is the semi-major axis. (where a2 > b2)
Given that a = ±5, c = ±4
As, from the relation
c2 = a2 – b2 (when a2 > b2)
b2 = a2 – c2
b2 = 25 – 16
b2 = 9
So, a2 = 25 and b2 = 9
Hence, the required equation of ellipse,
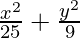 = 1
= 1
Question 11. Vertices (0, ± 13), foci (0, ± 5).
Solution:
Since the vertices are on y-axis, the equation will be of the form
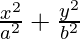 = 1, where b is the semi-major axis. (where a2 < b2)
= 1, where b is the semi-major axis. (where a2 < b2)
Given that b = ±13, c = ±5
As, from the relation
c2 = b2 – a2 (when a2 < b2)
a2 = b2 – c2
a2 = 169 – 25
a2 = 144
So, a2 = 144 and b2 = 169
Hence, the required equation of ellipse,
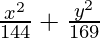 = 1
= 1
Question 12. Vertices (± 6, 0), foci (± 4, 0).
Solution:
Since the vertices are on x-axis, the equation will be of the form
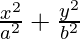 = 1, where a is the semi-major axis. (where a2 > b2)
= 1, where a is the semi-major axis. (where a2 > b2)
Given that a = ±6, c = ±4
As, from the relation
c2 = a2 – b2 (when a2 > b2)
b2 = a2 – c2
b2 = 36 – 16
b2 = 20
So, a2 = 36 and b2 = 20
Hence, the required equation of ellipse,
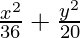 = 1
= 1
Question 13. Ends of major axis (± 3, 0), ends of minor axis (0, ± 2).
Solution:
Since the major axis are on x-axis, and minor axis on the y-axis, the equation will be of the form
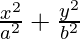 = 1, where a is the semi-major axis. (where a2 > b2)
= 1, where a is the semi-major axis. (where a2 > b2)
Given that a = ±3, b = ±2
So, a2 = 9 and b2 = 4
Hence, the required equation of ellipse,
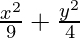 = 1
= 1
Question 14. Ends of major axis (0, ±√5), ends of minor axis (± 1, 0).
Solution:
Since the major axis are on y-axis, and minor axis on the x-axis, the equation will be of the form
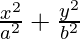 = 1, where b is the semi-major axis. (where a2 < b2)
= 1, where b is the semi-major axis. (where a2 < b2)
Given that a = ±1, b = ±√5
So, a2 = 1 and b2 = 5
Hence, the required equation of ellipse,
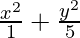 = 1
= 1
Question 15. Length of major axis 26, foci (± 5, 0).
Solution:
Since the foci are on x-axis, the equation will be of the form
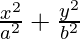 = 1, where a is the semi-major axis. (where a2 > b2)
= 1, where a is the semi-major axis. (where a2 > b2)
Given that c = ±5 and Length of major axis = 26
As, Length of major axis = 2a (when a2 > b2)
2a = 26
a = 13
As, from the relation
c2 = a2 – b2 (when a2 > b2)
b2 = a2 – c2
b2 = 169 – 25
b2 = 144
So, a2 = 169 and b2 = 144
Hence, the required equation of ellipse,
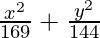 = 1
= 1
Question 16. Length of minor axis 16, foci (0, ± 6).
Solution:
Since the foci are on y-axis, the equation will be of the form
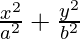 = 1, where b is the semi-major axis. (where a2 < b2)
= 1, where b is the semi-major axis. (where a2 < b2)
Given that c = ±6 and Length of minor axis = 16
As, Length of minor axis = 2a (when a2 < b2)
2a = 16
a = 8
As, from the relation
c2 = b2 – a2 (when a2 < b2)
b2 = c2 + a2
b2 = 36 + 64
b2 = 100
So, a2 = 64 and b2 = 100
Hence, the required equation of ellipse,
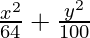 = 1
= 1
Question 17. Foci (± 3, 0), a = 4.
Solution:
Since the foci are on x-axis, the equation will be of the form
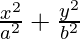 = 1, where a is the semi-major axis. (where a2 > b2)
= 1, where a is the semi-major axis. (where a2 > b2)
Given that a = 4 and c = ±3
As, from the relation
c2 = a2 – b2 (when a2 > b2)
b2 = a2 – c2
b2 = 16 – 9
b2 = 7
So, a2 = 16 and b2 = 7
Hence, the required equation of ellipse,
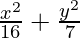 = 1
= 1
Question 18. b = 3, c = 4, centre at the origin; foci on the x axis.
Solution:
Since the foci are on x-axis, the equation will be of the form
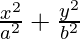 = 1, where a is the semi-major axis. (where a2 > b2)
= 1, where a is the semi-major axis. (where a2 > b2)
Given that b = 3 and c = 4
As, from the relation
c2 = a2 – b2 (when a2 > b2)
a2 = b2 + c2
a2 = 9 + 16
a2 = 25
So, a2 = 25 and b2 = 9
Hence, the required equation of ellipse,
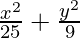 = 1
= 1
Question 19. Centre at (0,0), major axis on the y-axis and passes through the points (3, 2) and (1, 6).
Solution:
The standard equation of ellipse having centre (0, 0) will be of the form
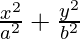 = 1
= 1
Since the points (3, 2) and (1, 6) lie on the ellipse, we can have
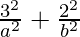 = 1
= 1
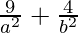 = 1 -(1)
= 1 -(1)
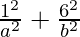 = 1
= 1
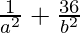 = 1 -(2)
= 1 -(2)
Eq(2) subtracted from (multiplying eq(1) by 9) and, we get
9×(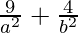 ) – (
) – (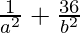 ) = 9 – 1
) = 9 – 1
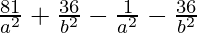 = 8
= 8
80/a2 = 8
a2 = 80/8
a2 = 10
Now, substituting a2 = 10 in eq(1)
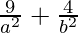 = 1
= 1
9/10 + 4/b2 = 1
4/b2 = 1 – 9/10
4/b2 = 1/10
b2 = 10 × 4 = 40
So, a2 = 10 and b2 = 40
Hence, the required equation of ellipse,
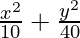 = 1
= 1
Question 20. Major axis on the x-axis and passes through the points (4, 3) and (6, 2).
Solution:
The standard equation of ellipse having centre (0, 0) will be of the form
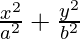 = 1
= 1
Since the points (4,3) and (6,2) lie on the ellipse, we can have
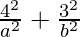 = 1
= 1
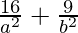 = 1 -(1)
= 1 -(1)
and, 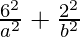 = 1
= 1
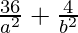 = 1 -(2)
= 1 -(2)
(multiplying eq(2) by 9) subtracted from (multiplying eq(1) by 4) and, we get
9×(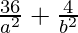 ) – 4×(
) – 4×(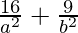 ) = 9 – 4
) = 9 – 4
 = 5
= 5
260/a2 = 5
a2 = 260/5
a2 = 52
Now, substituting a2 = 52 in eq(1)
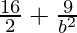 = 1
= 1
9/b2 = 1 – 16/52
9/b2 = 36/52
9/b2 = 36/52
b2 = 9 × 36/52 = 13
So, a2 = 52 and b2 = 13
Hence, the required equation of ellipse,
 = 1
= 1
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...