Algebraic Expressions and Identities | Class 8 Maths
Last Updated :
27 Oct, 2020
In mathematics, an algebraic expression is an expression built up from integer constants, variables, and algebraic operations. This article is about Expressions and Identities in Algebra. In order to understand these terms, we need to have an understanding of terms, factors, and coefficients. There are many types of expressions and identities that are discussed in detail
Basic Terminology
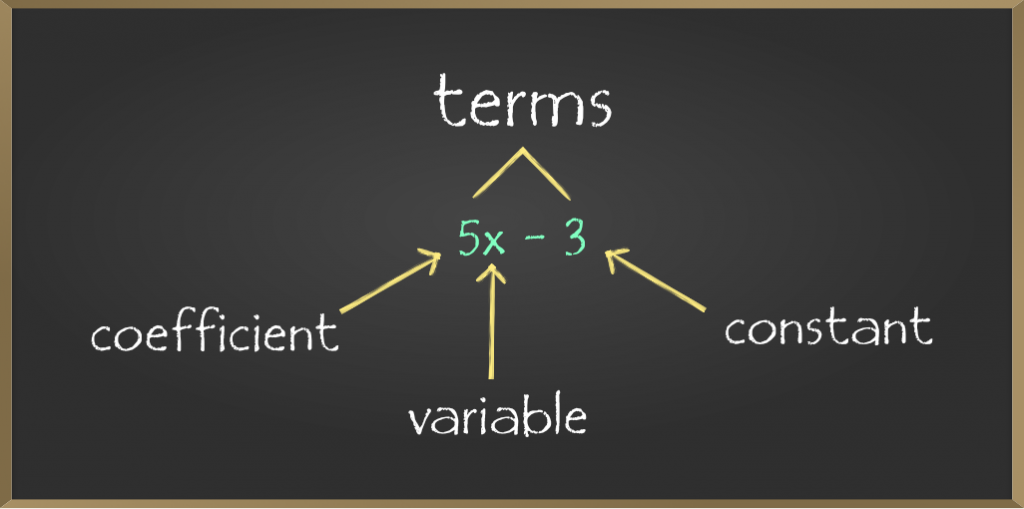
Terms: In algebra, a term can be a variable or a constant or a constant multiplied by a variable.
Example: 3x, 4, xy.
Factors: In algebra, factors are all the possible parts of the product.
Note: 1 is a factor for everything.
Example 1: Factors of 5x are 1,5,x, and 5x.
Example 2: Factors of 6x(y+7) are 1,6,x, y+7.
Coefficients: In algebra, When a term is formed when a constant multiplied by a variable or variables, that constant is called a coefficient.
Example1: 5x: In this term, 5 is the coefficient.
Reason: As 5 is a constant and is being multiplied to a variable ‘x’ by definition ‘5’ is called a coefficient.
Example 2: 3x+4y: In this expression, 3, 4 are coefficient.
Reason: s 3 and 4 are constants and are being multiplied to a variable ‘x’ and ‘y’ so by definition ‘3,4’ are called as coefficients.
Expressions in Algebra
An algebraic expression is an expression that is made up of variables and constants, along with algebraic operations (like subtraction, addition, multiplication, etc.). Expressions are made up of terms.
Example: 5x+20y, 6-8x.
Types of Expression in Algebra
Expressions in Algebra are divided into three types based on the number of Terms involved in the expression. These types are:
- Monomial Expression
- Binomial Expression
- Polynomial Expression
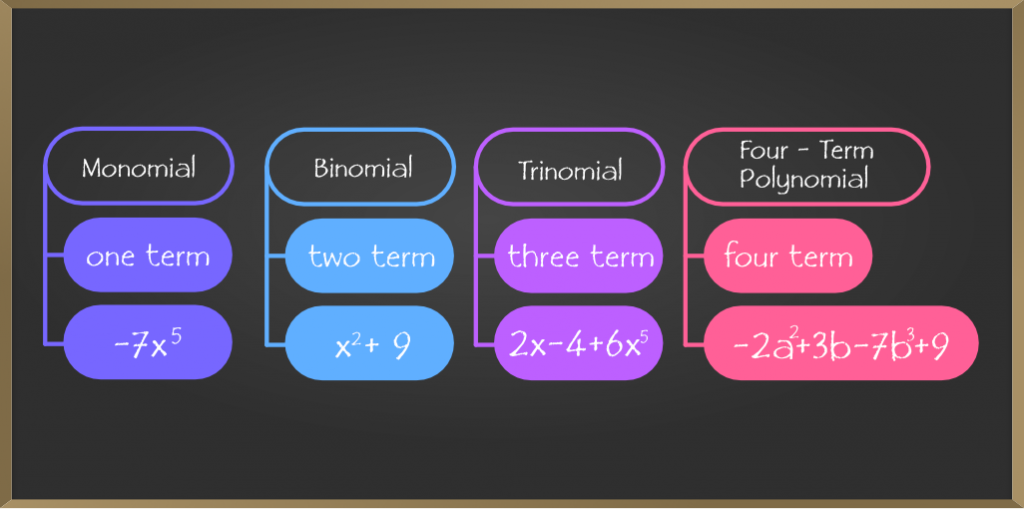
Monomial Expression
Algebraic expressions that contain only one term are called Monomial Expressions.
Examples: 5x, 10y, 25yz, etc.

Binomial Expression
Algebraic expression which has two terms (different or unlike terms) is called binomial expression.
Examples: 30xy+60, 25x+24y, 7+8yz, etc.

Polynomial Expression
Algebraic expression which contains more than one term with non-negative integer exponents is called Polynomial Expression.
Examples: 2x+3y+4z, 10x+20y+45,etc.
Basic Algebraic Identities
In algebra, if equality holds true for all variables then it is defined as an identity. In general, there are 4 basic Identities, and using this we can create many different identities.

Example: Implement the first Identity on x = 4, and y = 3
Solution:
Applying the identity:
L.H.S => (x+y)2 = (4+3)2
= (7)2
= 49
R.H.S => 42 +32+ 2 (4) (3) = 49
As L.H.S = R.H.S, this identity is verified and true.

Example: Implement the second Identity on x = 4, and y = 3
Solution:
Applying the identity:
L.H.S => (x – y)2 = (4 – 3)2
= (1)2
= 1
R.H.S => 42 + 32 – 2 (4) (3) = 1
As L.H.S = R.H.S, this identity is verified and true.

Example: Implement the third Identity on x = 4, and y = 3
Solution:
Applying the identity:
L.H.S => (x + y)(x – y) = (4 + 3)(4 – 3)
= (7)(1)
= 7
R.H.S : x2 – y2 = (4)2 – (3)2
= 16 – 9
= 7
As L.H.S = R.H.S, this identity is verified and true.

Example: Implement the fourth Identity on x = 3, y = 4, and z = 5.
Solution:
Applying the identity:
L.H.S => (x + y + z)2 = (3 + 4 + 5)2
= (12) 2
= 144
R.H.S => x2 – y2 = (3)2 + (4)2 + (5)2 + 2(3)(4) + 2(4)(5) + 2(5)(3)
= 144
As L.H.S = R.H.S, this identity is verified and true.
Using the above Identities we can derive many identities, some of the popularly used identities are written below:
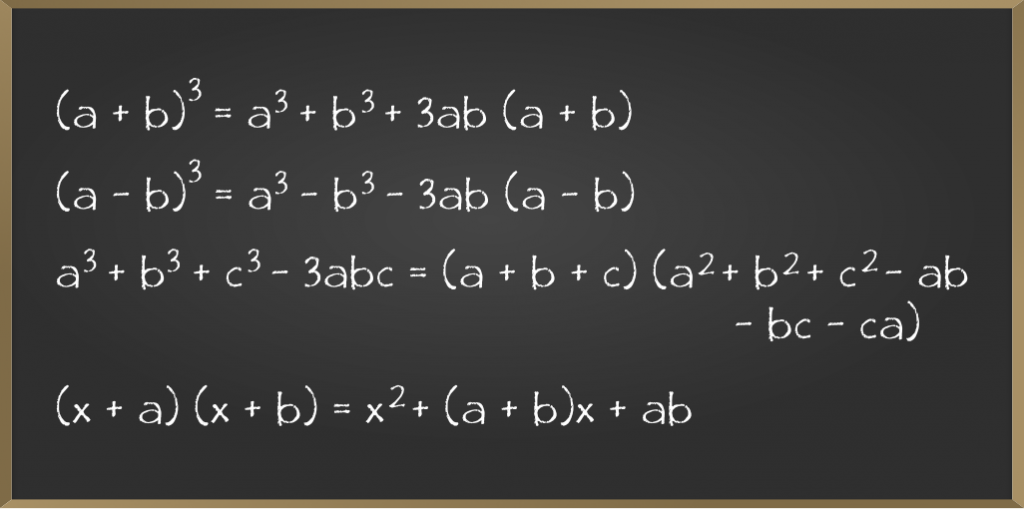
Share your thoughts in the comments
Please Login to comment...