Distance Formula in 3D calculates the distance between two points, a point and a line, and a point and a plane in three-dimensional coordinates as well as a two-dimensional Cartesian Plane. This article deals with the distance formula of points in three-dimensional space. In three dimensions, a point is represented as P(x, y, z). In this article, we will learn the 3D Distance formula, its derivation, and solved examples based on it.
What is 3D Distance Formula?
The 3D Distance formula is used to calculate the distance between two points, a point, and a line, and between a point and a plane in a three-dimensional space. 3D geometry comes into the picture to model real-world quantities such as velocity, fluid flows, electrical signals, and many other physical quantities. 3D geometry deals with three coordinate points represented using three coordinate axes namely x, y, and z which are mutually perpendicular. In 3D Distance Formula we will learn the 3D Distance formula for the following cases:
- Distance between Two Points in 3D
- Distance between a Point and Origin in 3D
- Distance of Point From a Line
- Distance Between Parallel Lines
- Distance of a Point from a Plane
Distance between Two Points in 3D
For two points P(x1, y1, z1) and Q(x2, y2, z2) located in three dimensional space, the 3D distance formula is given as

In case of origin one of the points will be O(0, 0, 0) and hence we will use x1 = 0, y1 = 0 and z1 = 0 in the formula to calculate the distance.
Example: Find the distance between two points P(2, 5, 6) and Q(3, 4, 7)
Answer:
For point P, x1 = 2, y1 = 5, z1 = 6
For point Q, x2 = 3, y2 = 4, z2 = 7
Distance between P and Q is given as
PQ = √[(x2 – x1)2 + (y2 – y1)2 + (z2 – z1)2]
Now filling the values of coordinates in the above formula we get
PQ = √[(3 – 2)2 + (4 – 5)2 + (7 – 6)2]
⇒ PQ = √(1 + 1 + 1) = √3 units
Distance between a Point and Origin in 3D
Like 2D system we can also calculate the distance between a point and origin. In 3D system the coordinates of origin is given as O(0, 0, 0). Hence, we need to put the values of x1 = 0, y1 = 0 and z1 = 0 or even can chose x2, y2 and z2 to be zero as this does not cause any change is the value. The distance formula to calculate the distance between a point and origin in 3D is given in the image attached below:

Example: Calculate the distance between P(-1, 2, 4) and origin O.
Solution:
We know that the coordinates for origin is O(0, 0, 0)
Hence, the Distance between origin O(0, 0, 0) and P(-1, 2, 4) is given as
OP = √(x2 + y2 + z2)
⇒ OP = √{(-1)2 + 22 + 42}
⇒ OP = √{1 + 4 + 16} = √21 units
Derivation of 3D Distance Formula between Two Points
The derivation of 3D Distance Formula can be understood with the help of the following image.

Let there be two points P(x1, y1, z1) and Q(x2, y2, z2) in three-dimensional space and are part of rectangular axes. Through Points P and Q draw planes parallel to the coordinate plane. Thus we get a rectangular parallelepiped in which PQ is body diagonal.
Consider Point A adjacent to Q such that AP is face diagonal. Now, AP is along one of the coordinate axes, hence AP is perpendicular to AQ.
Using Pythagoras Theorem
PQ2 = AP2 + AQ2 ….. (i)
Now take a point M adjacent to P and A such that MQ is a body diagonal
AP2 = AM2 + PM2 ……(ii)
Putting the values of AP2 from (ii) to (i)
⇒ PQ2 = AM2 + PM2 + AQ2
PM = x2 – x1
AQ = y2 – y1
AM = z2 – z1
Hence,
PQ2 = (x2 – x1)2 + (y2 – y1)2 + (z2 – z1)2
Hence, if PQ = d
then distance formula between two points in 3D is given as
d2 = (x2 – x1)2 + (y2 – y1)2 + (z2 – z1)2
⇒ d = √[(x2 – x1)2 + (y2 – y1)2 + (z2 – z1)2]
If the distance is measured from the origin then the 3D Distance formula is given as
d = √(x2 + y2 + z2)
Example 1: Find the distance between the points P(1, –3, 4) and Q (– 4, 1, 2).
Solution:
Using the formula to calculate the distance between point P and Q,
Distance (d) = √[(x2 – x1)2 + (y2 – y1)2 + (z2 – z1)2]
d = √[(-4-1)2+(1+3)2+(2-4)2] = √(25 + 16 + 4) = √45 units
Example 2: Show that the points P (–2, 3, 5), Q (1, 2, 3), and R (7, 0, –1) are collinear.
Solution:
We know that points are said to be collinear if they lie on a line.
PQ = √{(1+2)2 + (2-3)2 + (3-5)2} = √{9+1+4} = √14 units
QR = √{(7-1)2 + (0-2)2+(-1-3)2} = √{36+4+16} = √56 = 2√14
PR = √{(7+2)2 + (0-3)2 + (-1-5)2} = √{81+9+36} = √126 = 3√14
As PQ + QR = PR
Hence P, Q, and R are collinear.
Distance of Point From a Line
The distance of a point from a line is the perpendicular distance from the point to the line.
Suppose we have to find the distance of a point P(x0, y0, z0) from line l, then the formula is,
Distance (d) = 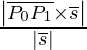
Where ‘s’ is the directing vector of line l.
Example: Find the distance from point P(-6, 1, 21) to a line 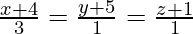 ?
?
Solution:
Let Line L : 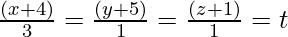
P(-6, 1, 21) and P'(3t-4, t-5, t-1)
⇒ 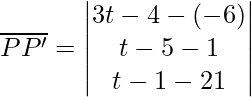
⇒ 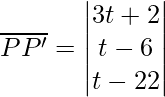
Now, 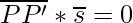
⇒ 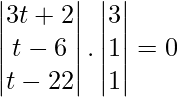
⇒ 9t + 6+t -6+t-22 = 0, 11t – 22=0 and t=2
⇒ 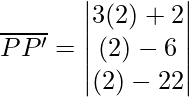
⇒ 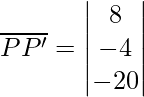
⇒ 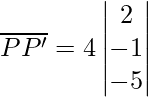
⇒ d = 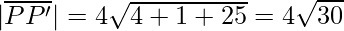
Distance of a Point from a Plane
The distance from a point to a plane is the perpendicular distance from a point on a plane.

If Qx + Ry + Sz + T = 0 is a plane equation, then the distance from point P(Px, Py, Pz) to the plane can be found using the following formula:
Distance (d) = 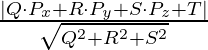
Example: Find the distance between plane 2x + 4y – 4z – 6 = 0 and point P(0, 3, 6)?
Solution:
Using the formula:
Distance (d) = 
⇒ d = 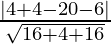
⇒ d = |-18|/√36 = 18/6 = 3
Distance Between Parallel Lines
The distance between any two parallel lines is the perpendicular distance from any point on one line to the other line.

Suppose there are two parallel lines y = mx + c1 and y = mx + c2, then the formula is,
Distance (d) =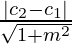
If the equation of two parallel lines is given as:
ax + by + d1 = 0 and ax + by + d2 = 0, then the formula is,
Distance (d) = 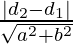
Where a and b are the coefficients of variables x and y in the line.
Example 1: Find the distance between parallel lines y = 2x + 10 and y = 2x + 12.
Solution:
The lines y = 2x + 10 and y = 2x + 12 are in form y = mx + c.
Where c1 = 10, c2 = 12, m = 2
Using formula, the distance (d) = |12-10|/√(1 + 22) = 2/5
Example 2: Find the distance between two parallel lines 4x + 3y + 6 = 0 and 4x + 3y – 3 = 0
Solution:
The lines given are 4x + 3y + 6 = 0 and 4x + 3y – 3 = 0. Both lines are in the form ax + by + d = 0.
Hence, d1 = 6, d2 = −3, a = 4, b = 3
Using the formula for this case, distance (d) will be calculated as:
⇒ d = 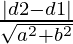
⇒ d = 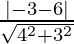
⇒ d = |-9|/√(16 + 9)
⇒ d = 9/√25
⇒ d = 9/5
Read More,
Practice Questions on 3D Distance Formula
Q1: Calculate the distance between the points P(-1, 0, 1) and Q(2, -1, 3)
Q2: Calculate the distance of the point (3, -5, 4) from the Origin.
Q3: Calculate the distance between the plane x + 2y – z + 3 = 0 and the Point (1, -2, 1)
Q4: Calculate the distance between two parallel lines 3x + 2y + 5 = 0 and 3x + 2y + 6 = 0
FAQs on 3D Distance Formula
1. How is a Point represented in 3D?
A Point is represented in 3D by using three coordinates as P(x, y, z) where, x, y, z are the coordinates of point P along the x, y, and z axis
2. What is 3D Distance Formula?
The 3D Distance Formula is used to calculate the distance between two points, between a point and a line, and between a point and a plane in three-dimensional space.
3. What is the Distance Formula between Two Points in 3D?
The distance formula between two points is 3D is given as PQ = √[(x2 – x1)2 + (y2 – y1)2 + (z2 – z1)2]
4. What is the Distance Formula between a Point and the Origin in 3D?
The Distance between a point and origin in 3D is given as PO = √(x2 + y2 +z2)
5. How to Derive Distance Formula for Two Points in 3D?
The distance formula for two points in 3D can be derived by drawing planes parallel to the coordinate axes such that the distance between two points appears as a part of a rectangular parallelepiped. The detailed derivation has been discussed under the heading ‘Derivation of Distance Formula Between Two Points in 3D’.
Share your thoughts in the comments
Please Login to comment...