Distance Formula in Coordinate Geometry is used to compute the distance between two points, a point, and a line, and two line segments. The distance formula is based on the Pythagorean theorem. In the formula, d represents the distance, y2 is the y-coordinate of the second point, y1 is the y-coordinate of the first point, x2 is the x-coordinate of the second point, and x1 is the x-coordinate of the first point.
Coordinate geometry, commonly referred to as analytic geometry or Cartesian geometry, is a branch of geometry based on a coordinate system. Its applications include physics, engineering, air travel, rocketry, space research, and spaceflight.
In this article, we will learn about the distance between two points in coordinate geometry, the formula for the distance between two points, a point, a line, a point and a plane, and others in detail.
Distance Formula in coordinate geometry is an important mathematical formula to calculate the distance between two points, two lines, two planes, a point, and a line, and a line and a plane. For instance, Distance Formula can be used to calculate the distance between two points of the let’s say XY plane. An ordered pair (x, y) represents the coordinate of the point, where the x-coordinate is defined as the distance of the point from the x-axis and the y-coordinate is the distance of the point from the y-axis. The x coordinate of the point is known as the abscissa whereas the y coordinate is known as the ordinate.
Distance Between Two Points Formula Definition
Distance formula is a mathematical formula used to calculate the distance between two points in a two-dimensional or three-dimensional space. It is a fundamental concept in geometry and can be applied in various fields, including physics, engineering, and computer science.
The lengths of the sides of triangles are also computed using the distance formula. The type of triangle, scalene, isosceles or equilateral can also be determined using the distance formula.
Coordinate Distance Calculator
To calculate the distance between two points on a 2D cartesian plane, use the below calculator:
Distance formula in math is used to find the distance between two points either in 2D or in 3D. The respective distance formula in 2D and 3D is discussed below in the article.
Distance between two points in a two-dimensional Cartesian coordinate system (or Euclidean space) can be calculated using the distance formula.
Let’s say you have two points: P (x1,y1) and Q (x2,y2).
Distance d between P and Q is given by the formula:
d = √ [(x2−x1)2 + (y2−y1)2]
In words, to find the distance between two points, you subtract the x-coordinates and square the result, then subtract the y-coordinates and square the result. Add these squared values together, and then take the square root of the sum.
This formula is derived from the Pythagorean theorem applied to the right triangle formed by the line segment connecting the two points and the coordinate axes.
The distance between two points is always a positive value or zero.
The Distance Formula used to find the distance between two points in a 2D plane is given as follows:
Consider any two arbitrary points A (x1, y1) and B (x2, y2) on the given coordinate axis. The distance between the following two points is given by the following Distance Formula:

d = √{ (x2 – x1)2 + (y2 – y1)2 }
Derivation of Distance Formula
Derivation of the Distance Formula is given using the Pythagoras Theorem. In the right-angled triangle ABC, we have:
AB2 = AC2 + BC2
Distance between points A and C is (x2 – x1)
Distance between points B and C is (y2 – y1)
Distance, d is calculated as:
d2 = (x2 – x1)2 + (y2 – y1)2
Now,
Taking the square root on both sides,
d = √[(x2 – x1)2 + (y2 – y1)2]
Thus, d is the distance between two points.
In a 3D plane, we use three coordinates to define the position of any point. Now to find the distance between two points in 3D lets first take two points A (x1, y1, z1) and B (x2, y2, z2) then the shortest distance between these two points AB in 3D is given using the Distance Formula:
d = √[(x2 – x1)2 + (y2 – y1)2 + (z2 -z1)2]
where d is the shortest distance between points A and B.
Example: Find the distance between point A (2, 5, 6) and point B (3, 4, 8).
Solution:
Distance between points A and B is given using the formula,
d = √[(x2 – x1)2 + (y2 – y1)2 + (z2 -z1)2]
given points, A (2, 5, 6) and B (3, 4, 8), comparing with A (x1, y1, z1) and B (x2, y2, z2)
we get, x1 = 2, y1 = 5, z1 = 6 and x2 = 3, y2 = 4, z2 = 8 substituting these values in the above formula we get,
d = √[(3-2)2 + (4-5)2 + (8-6)2]
⇒ d = √[(1)2 + (-1)2 + (2)2]
⇒ d = √[1 + 1 + 4]
⇒ d = √(6) unit
Distance between Two Points in Polar Co-ordinates
We can also calculate the distance between two points using the polar coordinates.
Let’s take two points A (r1, θ1) and B (r2, θ2) then the distance between them is calculated using the Distance Formula:
AB = √[(r1)2 + (r2)2 – 2r1r2 cos (θ1 – θ2)]
The shortest distance between a point and a line can easily be calculated using the distance formula discussed in this section of the article. The distance between a point and the line can be in 2D or 3D space.
Let’s learn about the distance of a point to a line in 2D and 3D in this article.
Distance Formula From a Point To a Line in 2D
The distance between a point and a line in 2D is calculated using the formula discussed below:

Let’s take a point (x1, y1) and a line ax + by + c = 0 then the distance between them is given using the Distance Formula:
d = [Tex]\frac{|ax_1+by_1+c|}{\sqrt{a^2+b^2}}
[/Tex]
Distance Formula From a Point To a Line in 3D
We can also calculate the distance of a point from the line in the 3D plane.
Let’s take a point A (x1, y1, z1) and a line (x – x2)/a = (y – y2)/b = (z – z2)/c in the 3D plane then the distance between them is given using the Distance Formula:
[Tex]\bold{d= \frac{|\vec{AB} × \vec{s}|}{| \vec{s}|}}
[/Tex]
Where,
- A is the point (x1, y1, z1) from which the distance is to be calculated
- Q is the point (x2, y2, z2) on the line L from which distance is calculated
- [Tex]\bold{\vec{AB}}[/Tex] is (x2 -x1, y2 – y1, z2 – z1)
- [Tex]\bold{\vec{s}}[/Tex] is the direction vector of the line <a, b, c>
Distance Between Two Lines
Distance Formula Between Two Lines
The distance between two parallel lines in 2D or 3D can be calculated using various formulas, some of which are discussed below:
Distance Formula Between Two Parallel Lines in 2D
The distance between two parallel lines is given by the Distance Formula, let’s take two parallel line ax + by + c1 = 0 and ax + by + c2 = 0

[Tex]\bold{d = \frac{|c_2-c_1|}{\sqrt{a^2+b^2}}}
[/Tex]
Shortest Distance Between Two Skew Lines in 3D
In 3D lines can be:
- Parallel lines
- Skew Lines
- Intersecting Lines
Skew lines are the lines that are at a specific distance apart from one another in 3D space.
Let’s take two lines L1 is (x – x1)/a1 = (y – y2)/b1 = (z – z1)/c1 and L2 is (x – x2)/a2 = (y – y2)/b2 = (z – z2)/c2 then the distance between them is given using the Distance Formula:

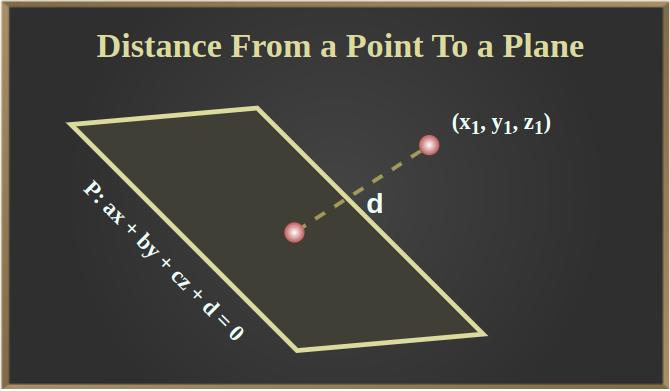
Distance From a Point To a Plane
Distance Formula From a Point To a Plane
In 3D we can also calculate the distance between a point and the plane using the distance formula.
Let’s take point A (x1, y1, z1) and plane P: ax + by + cz + d = 0 then the distance between the point and the plane is given using the Distance Formula:
d = |ax1 + by1 + cz1| / √(a2 + b2 + c2)
The image below shows the distance between the point and the plane:
Distance Between Two Parallel Planes
Distance Formula Between Two Parallel Planes
3D formulas are used to find the distance between two parallel planes.
Let’s take two parallel planes P1: ax + by + cz + d1 = 0 and the plane P2: ax + by + cz + d2 = 0 then the distance between the planes is given using the following Distance Formula:
d = |d2 – d1| / √(a2 + b2 + c2)
The image below shows the distance between two parallel planes:

Distance Formula has various applications in Mathematics, Sciences, and others and some of the most important applications of the Distance Formula are:
- Distance of a point from the origin is calculated using the Distance Formula.
- Distance between two points in 2D and 3D planes is calculated using the Distance Formula.
- The magnitude of the vector is calculated using the Distance Formula.
- The magnitude of the complex number is calculated using the Distance formula.
Apart from this distance formula also has some real-life applications which are:
- Distance Formula is used to find the distance between two stars.
- Distance Formula is also used to find the distance between various points in the sea and oceans.
- Distance Formula is used to find the linear distance between two points in the Globe.
Question 1: Calculate the distance between the points X(5, 15) and Y(4, 14).
Solution:
Distance between point X and Y is given by distance formula
d = √[( x2 – x1 )2 + ( y2 – y1 )2]
⇒ d = √[( 4 – 5 )2 + ( 14 – 15 )2]
⇒ d = √[( 1 )2 + ( 1 )2]
⇒ d = √(2)
Distance between X and Y is √2 or 1.41
Question 2: Find the distance between the parallel lines -6x + 20y + 10 = 0 and -6x + 20y + 20 = 0.
Solution:
General equation of parallel lines is
Ax + By + C1 = 0 and Ax + By + C2 = 0,
Here,
A = -6, B = 20, C1 = 10, and C2 = 20
Applying formula
d = [Tex]\frac{|c_2-c_1|}{\sqrt{a^2+b^2}}
[/Tex]
⇒ d = [Tex]\frac{|20-10|}{\sqrt{-6^2+20^2}}\\ \frac{|10|}{\sqrt{36+400}}\\ \frac{10}{\sqrt{436}}
[/Tex]
⇒ d = 10 / √436
Thus, the distance between two parallel lines is d = 10 / √436
Question 3: Calculate the distance between line 4a + 6b – 26 = 0 from the point (2, –4) using the Distance Formula in maths.
Solution:
General equation of parallel lines is
A point (x1, y1) and a line ax + by + c = 0
Here,
A = 4, B = 6 and C = –26
Applying formula
d = [Tex]\frac{|ax_1+by_1+c|}{\sqrt{a^2+b^2}}
[/Tex]
⇒ d = [Tex]\frac{|4\times2+6\times(-4)+(-26)|}{\sqrt{4^2+6^2}}\\ =\frac{8-24-26}{\sqrt{16+36}}\\ =\frac{-42}{\sqrt{52}}
[/Tex]
⇒ d = -42 / √52
Thus, the distance between lines and point is d = -42 / √52
Question 4: Calculate the distance between points A(-25, -5) and B(-16, -4) using the Distance Formula in Maths.
Solution:
Distance between point A and B is given by distance formula
d = √[( x2 – x1 )2 + ( y2 – y1 )2]
⇒ d = √[( (-16) – (-25) )2 + ( (-4) – (-5) )2]
⇒ d = √[( 9 )2 + ( 1 )2]
⇒ d = √(82)
Distance between A and B is √82 or 9.05
1. A square has one vertex at (1, 1) and the opposite vertex at (4, 4). Calculate the length of the diagonal.
2. Calculate the distance between the points (-5, -5) and (-1, -1).
3. Find the distance between the points (2, -3) and (-4, 5).
4. Two points, A and B, have coordinates (2, 3) and (10, 7) respectively. A third point, C, lies on the line segment AB and divides it into a ratio of 2:1. Find the coordinates of point C and calculate the distance from C to point A.
5. Calculate the distance between the points (1, 2, 3) and (4, 6, 9).
6. Two vertices of a cube are (0, 0, 0) and (3, 3, 3). Determine the length of the diagonal that connects these two vertices inside the cube.
What is distance formula in maths?
The distance formula in maths is used to find the distance between two points. If we have to find the distance between two points A (x1, y1) and B (x2, y2) then the formula is:
AB = √[(x2−x1)2+(y2−y1)2]
How is Pythagorean Theorem related to the distance formula?
The distance between two points (x1,y1) and (x2,y2) is calculated by:
Distance2 = (x2−x1)2+(y2−y1)2
Distance = √[(x2−x1)2+(y2−y1)2]
What is Manhattan distance formula?
Manhattan Distance is the distance measured between two points along the right angular axis. Manhattan Distance between two points (x1, y1) and (x2, y2) is given by the formula:
D = |x2 – x1| + |y2 – y1|
What is coordinate of a point?
Ordered pair (x,y) which is used to know the position of any point in the Cartesian plane is called the coordinate point. For example, (1,3) is a coordinate point.
What is distance formula in coordinate geometry?
The distance formula gives the shortest distance between two points in the coordinate geometry. The formula between the two points is given by:
d = √[(x2−x1)2+(y2−y1)2]
What is the formula for distance from origin?
The distance of any point P (x1, y1) from the origin O (0,0) is calculated using the formula:
OP = √[(x1)2 + (x2)2]
What are different distance formulas in maths?
There are a number of distance formulas in maths including distance between two points, distance formula between point and a line, distance formula between two points etc.
How to calculate distance between two points?
To calculate the distance between two points in a two-dimensional Cartesian coordinate system, you use the distance formula: d = √[(x2−x1)2+(y2−y1)2]. In this formula, (x1, y1) and (x2, y2) represent the coordinates of the two points. You subtract the x-coordinates of the points, square the result, then subtract the y-coordinates and square the result. Add these squared values together, and finally, take the square root of the sum.
How to find distance between two points on a graph?
To find the distance between two points on a graph, you first locate the coordinates of the two points on the graph. Then, you can use the distance formula mentioned above to calculate the distance between them. This involves subtracting the x-coordinates of the points, squaring the result, subtracting the y-coordinates and squaring the result, adding these squared values together, and finally, taking the square root of the sum.
What is the shortest distance between two points?
In Euclidean geometry, the shortest distance between two points is a straight line. This is known as the Euclidean distance or the straight-line distance. It is the distance that would be traveled along a straight line between the two points, without any deviations or changes in direction. The distance formula mentioned above calculates the Euclidean distance between two points in a two-dimensional Cartesian coordinate system.
Share your thoughts in the comments
Please Login to comment...