Section Formula is a useful tool in coordinate geometry, which helps us find the coordinate of any point on a line which is dividing the line into some known ratio. Suppose a point divides a line segment into two parts which may be equal or not, with the help of the section formula we can find the coordinates of that point.
In this article, we will learn about section formulas, the types of division of lines, and how to solve problems based on them in detail.
Section formula is used to find the coordinates of a point that divides the line in a given ratio or to find the ratio in which the line is divided by a point of given coordinates. Any point can divide a line segment in two ways, either the point can be on the line segment and divide the line internally or the point can be on the extended line segment and divide the line segment externally. For these two case section formula is given differently which is as follows:
- Internal Section Formula
- External Section Formula
The following illustration shows the internal and external division of line segment AB by Point O.

When the point divides the line segment in the ratio m : n internally at point C then that point lies on the line segment i.e., C divides AB internally, then we can use the Internal Section formula to calculate coordinates of C with the help of ratio and coordinates of the endpoints A and B. It is also called Internal Division. The term ‘Sectional Formula’ is generally used for Internal Sectional Formula. If the coordinates of A and B are (x1, y1) and (x2, y2) respectively then Internal Section Formula is given as:
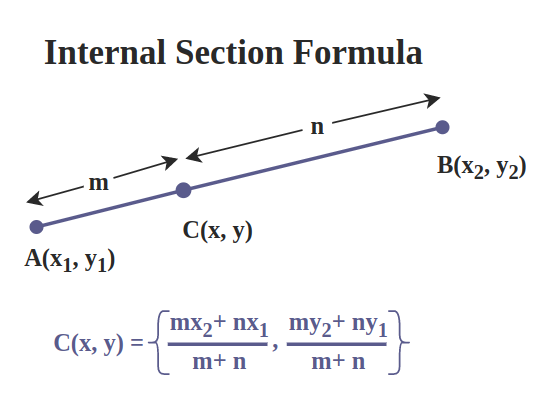
Let A(x1, y1) and B(x2, y2) be the endpoints of the given line segment AB and C(x, y) be the point that internally divides AB in the ratio m : n.
i.e., AC / CB = m / n
We want to find the coordinates of C (x, y). Take the given line segment and draw perpendiculars of A, C, and B parallel to Y coordinate joining at P, Q, and R on the X-axis as illustrated in the diagram below:

From above diagram,
AM = PQ = OQ – OP = (x – x1),
CN = QR = OR – OQ = (x2 – x),
CM = CQ – MQ = (y – y1),
and BN = BR – NR = (y2 – y)
Clearly, ∆AMC ∼ ∆CNB (As all angles are equal for both triangles)
Therefore, ratio of sides are same for similar triangles.
⇒ AC / CB = AM / CN = CM / BN
Now substituting the values in the above relation
⇒ m / n = [(x – x1)/(x2 -x)] = [(y – y1)/(y2 – y)]
⇒ m / n = [(x – x1)/(x2 -x)] and m / n = [(y – y1)/(y2 – y)]
Solving the 1st condition,
⇒ m(x2 – x) = n(x – x1)
⇒ (m + n)x = (mx2 + nx1)
⇒ x = (mx2 + nx1) / (m + n)
Solving the 2nd condition,
⇒ m(y2 – y) = n(y – y1)
⇒ (m + n)y = (my2 + ny1)
⇒ y = (my2 + ny1) / (m + n)
Therefore,

When the point which divides the line segment in the ratio m : n lies outside the line segment i.e., when we extend the line it coincides with the point, then we can use the External Section formula to calculate the coordinates of C. It is also called External Division. If the coordinates of A and B are (x1, y1) and (x2, y2) respectively then the external Section Formula is given as follows:

To derive the internal section we took a line segment and a point C(x, y) which lies on the line, but in the case of the external section formula, we have to take that point C(x, y) outside the line segment.
Let A(x1, y1) and B(x2, y2) be the endpoints of the given line segment AB and C(x, y) be the point that divides AB in the ratio m : n externally. To find the coordinates (x, y) of C takes the external divided line AB and draw perpendiculars from A, B, and C parallel to the y-axis joining at P, Q, and R on the x-axis and perpendicular from A and B parallel to the x-axis which meats the perpendicular drawn from C parallel to y-axis at M and N. The following diagram shows the complete construction.

From the diagram,
AM = PR = OR – OP = (x – x1),
BN = QR = OR – OQ = (x – x2),
CM = RC – MR = (y – y1),
and CN = CR – NR = (y – y2)
Clearly, ∆AMC ∼ ∆CNB (As all angles are equal for both triangles)
As, the ratio of all the sides are same for similar triangles.
⇒ AC / BC = AM / BN = CM / CN
Now substituting the values in the above relation
⇒ m/n = [(x – x1)/(x – x2)] = [(y – y1)/(y – y2)]
⇒ m/n = [(x – x1)/(x – x2)] and m/n = [(y – y1)/(y – y2)]
Solving the 1st condition,
⇒ m(x – x2) = n(x – x1)
⇒ (m – n)x = (mx2 – nx1)
⇒ x = (mx2 – nx1)/(m – n)
Solving the 2nd condition,
⇒ m(y – y2) = n(y – y1)
⇒ (m – n)y = (my2 – ny1)
⇒ y = (my2 – ny1)/(m – n)
Therefore,

When the point dividing the line segment joining the two points A and B coincide with the midpoint of the line segment, then this special case emerges. The section formula for this case is also referred to as the midpoint formula.
Let two points A(x1, y1) and B(x2, y2), and a point C(x, y) be the midpoint of the line segment AB i.e., AC : CB = 1:1, then the section formula becomes as follows:
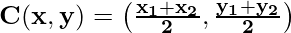
Read More,
Problem 1: Find the coordinates of point C (x, y) where it divides the line segment joining (4, – 1) and (4, 3) in the ratio 3 : 1 internally.
Solution:
Given coordinates are A (4, -3) and B (8, 5)
Let C (x, y) be a point which divides the line segment in the ratio of 3 : 1 i.e m : n = 3 : 1
Now using the formula C(x, y) = { (m × x2 + n × x1) / (m + n ) , (m × y2 + n × y1) / (m + n ) } as C is dividing internally.
⇒ C(x, y) = {(3×4 + 1×4 )/(3+1), (3×3 + 1×(-1))/(3+1)}
⇒ C(x, y) = {16/4, 8/4}
⇒ C(x, y) = {4, 2}
Hence, the coordinates are (4, 2).
Problem 2: If a point P(k, 7) divides the line segment joining A(8, 9) and B(1, 2) in a ratio m : n then find values of m and n.
Solution:
It is not mentioned that the point is dividing the line segment internally or externally. So, at that time we will consider the internal section as the default.
Given coordinates are A (8, 9) and B (1, 2)
Let the given point P (k, 7) divides the line segment in the ratio of m : 1
Using section formula for y coordinate.
⇒ 7 = (m y2 + n y1)/(m + n )
⇒ 7 = (m × 2 + 1 × 9)/(m + 1)
⇒ 7 = (2m + 9)/(m +1)
⇒ 7m + 7 = 2m +9
⇒ 5m = 2
⇒ m = 5 / 2
So the required ratio is 5 : 2
Therefore, value of m is 5 and value of n is 2
Problem 3: A (4, 5) and B (7, -1) are two given points, and point C divides the line-segment AB externally in the ratio 4 : 3. Find the coordinates of C.
Solution:
Given coordinates are A (4, 5) and B (7, -1)
Let C (x, y) be a point which divides the line segment externally in the ratio of 4 : 3 i.e m : n = 4 : 3
Now using the formula C(x, y) = { (m × x2 – n × x1) / (m – n) , (m × y2 – n × y1) / (m – n ) } as C is dividing internally.
C(x) = (mx2 – nx1)/(m – n)
⇒ C(x) = (4 × 7 – 3 × 4)/(4 – 3)
⇒ C(x) = (28 – 12)/(1)
⇒ C(x) = 16
C(y) = (my2 – ny1) / (m – n )
⇒ C(y) = (4 × (-1) – 3 × 5)/(4 – 3)
⇒ C(y) = (-4 – 15)/(1)
⇒ C(y) = -19
Hence, the required coordinates are (16, -19).
Problem 4: Find the coordinates of the midpoint of the line segment joining A(2, 5) and B(8, 1).
Solution:
Let P(x, y) be the mid point of line segment joining A(2, 5) and B(8, 1).
Then, P(x, y) =( (x1 + x2)/2, (y1 + y2)/2)
⇒ P(x, y) = ( (2 + 8)/2, (5 + 1)/2)
⇒ P(x, y) = (5, 3)
Therefore, the coordinates of the midpoint of the line segment AB are (5, 3).
Problem 5: Line 2x+y−4=0 divides the line segment joining the points A(2,−2) and B(3,7). Find the ratio of a line segment in which the line is dividing.
Solution:
Given coordinates are A (2, -2) and B (3, 7).
Let the line with equation 2x + y – 4 = 0 divides the line segment at point C (x, y)
As (x, y) lies on the the 2x + y – 4 = 0, so we can use same varible for this instance only.
Let us assume the given line cuts the line segment in the ratio 1 : n.
By section formula,
⇒ x = (m x2 + n x1)/(m + n)
⇒ x = (3 + 2n)/(1 + n) . . . (1)
Similarly,
⇒ y = (m y2 + n y1)/(m + n)
⇒ y = (7 – 2n)/(1 + n) . . . (2)
Now substituting the equations (1) and (2) in the given equation of the line.
⇒ 2x + y – 4 = 0
⇒ 2 [(3 + 2n)/(1 + n)] + [(7 – 2n)/(1 + n)] – 4 = 0
⇒ 6 + 4n + 7 − 2n − 4(1 + n) = 0
⇒ 13 + 2n − 4 − 4n = 0
⇒ 9 − 2n = 0
⇒ n = 2 / 9
Therefore the ratio at which the line divides is 9 : 2.
Note: We can also find the values of x and y by substituting the value of n in the equation (1) and (2).
Problem 6: Find the point P on the line joining A(2, 3) and B(5, 7) that is equidistant from points A and B.
Solution:
Let the coordinates of the point P be (x, y).
PA = √{(x-2)2 + (y-3)2)}
PB = √{(x-5)2 + (y-7)2}
As P is equidistant from A and B,
PA = PB
⇒ PA2 = PB2
⇒ (x-2)2 + (y-3)2= (x-5)2 + (y-7)2
⇒ x2+4 – 4x + y2 + 9 – 6y = x2 + 25 – 10x + y2 + 49 -14y
⇒ – 4x + 13 – 6y = 74 – 10x -14y
⇒ 6x + 8y = 61 . . .(1)
As line passing through two points (x1, y1) and (x2, y2) is given by:
y – y1 = [(y2 – y1) / (x2 – x1)](x – x1)
Thus, equation of line joining A(2, 3) and B(5, 7) is
y – 3 = [(7-3)(5-2)(x – 2)]
⇒ y – 3 = (4/3)(x-2)
⇒ 3y – 9 = 4x – 8
⇒ 3y – 4x = 1
⇒ y = (1 + 4x)/3 . . .(2)
Using the section formula, we can find the coordinates of the point P that satisfies this equation. Letting m = 1 and n = 1, we have:
Px = (x1 + x2) / 2 = (2 + 5) / 2 = 3.5
Py = (y1 + y2) / 2 = (3 + 7) / 2 = 5
Therefore, the coordinates of the point P that is equidistant from A and B are (3.5, 5).
Problem 7: A(2, 7) and B(–4, –8) are the coordinates of the line segment AB. There are two points that trisected the segment. Find their coordinates of them.
Solution:
TLet S(x1, y1) and T(x2, y2) be the two points, which divides the line segment AB into 3 equal parts i.e.,
AS = ST = TB . . . (1)
⇒ S divides the line segment AB in the ratio = AS/SB
⇒ Required ratio = AS/(ST + TB)
⇒ Required ratio = AS/(AS + AS) [from equation (1)]
⇒ Required ratio = AS/2 AS
⇒ Required ratio =1/2
So, S divides the line segment AB in the ratio of 1 : 2
Now applying section formula to find the coordinates of point S
⇒ x1 = (1 × (-4) + 2 × 2)/(1 + 2)
⇒ x1 = (-4 + 4)/3
⇒ x1 = 0
Similarly, for y coordinate,
⇒ y1 = (1 × (-8) + 2 × 7)/(1 + 2)
⇒ y1 = (14 – 8)/3
⇒ y1 = 2
Thus, S(x1, y1) = (0, 2)
Similarly T divides line segement AB in 2:1.
Now applying section formula to find the coordinates of point T
⇒ x2 = (2 × (-4) + 1 × 2)/(2 + 1)
⇒ x2 = (-8 + 2)/3
⇒ x2 = -2
Similarly, for y coordinate
⇒ y2 = (2 × (-8) + 1 × 7)/(2 + 1)
⇒ y2 = (-16 + 7)/3
⇒ y2 = -3
Thus, T (x2, y2) = (-2, -3)
Therefore the coordinates of required points are S (x1, y1) = (0, 2) and T (x2, y2) = (-2, -3).
What is Section Formula?
If a point C divides a line joining A(x1, y1) and B(x2, y2) internally in a ratio of m:n, then section formula is given as follows:

If a point C divides a line joining A(x1, y1) and B(x2, y2) externally in a ratio of m:n, then section formula is given as follows:

What is Internal Division of a line?
When a point lies on the line segement to divide it in some ratio, it is called internal division of line.
What is External Division of line?
When a point lies on the extented line segement to divide it in some ratio externally, it is called external division of line.
Can the Section Formula be used to find the Midpoint of a Line Segment?
Yes, section formula can be used to find the coodtinates of midpoint of a line segment, as mid point is the point which divides the line segment in 1:1.
What is the special case of the Section Formula for the Midpoint?
The case of midpoint of line segment is the special case of the section formula, and coordinates of midpoint of a line segment joining A(x1, y1) and B(x2, y2), is given as follows:
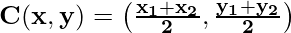
Share your thoughts in the comments
Please Login to comment...