Vector Calculus in Maths

Last Updated : 04 Sep, 2023

Vector Calculus in maths is a sub-division of Calculus that deals with the differentiation and integration of Vector Functions. We already know that Calculus is a branch of mathematics that deals with the rate of change of a function concerning another function. There are two major divisions of Calculus namely, Differential Calculus and Integral Calculus.

The branch of Differential Calculus deals with the process of finding derivatives or differentiation of functions while Integral Calculus deals with finding the antiderivative of a function whose derivative is given. In this article, we will learn in detail about Vector Calculus which is a lesser-known branch of calculus, and the basic formulas of Vector Calculus.

In this article, you are going to read everything about what is vector calculus in engineering mathematics, vector calculus formulas, vector analysis, etc.

Table of Content

What is Vector Calculus?
Operation in Vector
Divergence and Curl
Vector Calculus Formulas
Vector Calculus Identities
Vector Calculus Applications
Solved Examples
FAQs

What is Vector Calculus?

Vector Calculus is a branch of mathematics that deals with the operations of calculus i.e. differentiation and integration of vector field usually in a 3 Dimensional physical space also called Euclidean Space. The applicability of Vector calculus is extended to partial differentiation and multiple integration. Vector Field refers to a point in space that has magnitude and direction. These Vector Fields are nothing but Vector Functions. Vector calculus is also known as vector analysis.

The vector fields are the vector functions whose domain and range are not dimensionally related to each other. The branch of Vector Calculus corresponds to the multivariable calculus which deals with partial differentiation and multiple integration. This differentiation and integration of vector is done for a quantity in 3D physical space represented as R³. For n-dimensional space, it is represented as Rⁿ.

Vector Calculus Definition

Vector calculus, also known as vector analysis or vector differential calculus, is a branch of mathematics that deals with vector fields and the differentiation and integration of vector functions

Vector Calculus often called Vector Analysis deals with vector quantities i.e. the quantities that have both magnitude as well as direction. Since we know that Vector Calculus deals with differentiation and integration of functions, there are three types of integrals dealt with in Vector Calculus that are

Line Integral
Surface Integral
Volume Integral

Let’s learn about these integrals in detail.

Line Integral

Line Integral in mathematics is the integration of a function along the line of the curve. The function can be a scalar or vector whose line integral is given by summing up the values of the field at all points on a curve weighted by some scalar function on the curve. Line Integral is also called Path Integral and is represented by Φ = ∫_Lf. Line Integral has got its application in physics. For Example, Work Done by Force is along a path given as W = ∫_LF(s).ds because we know that work done is given as the product of force and distance covered.

Surface Integral

Surface Integral in mathematics is the integration of a function along the whole region or space that is not flat. In Surface integral, the surfaces are assumed of small points hence, the integration is given by summing up all the small points present on the surface. The surface integral is equivalent to the double integration of a line integral. Surface Integral has got its application in Electromagnetism and many more branches of physics where the vector function is spread over the surface. Surface Integral is represented as ∬_sf(x,y)dA.

Learn more about Double Integral.

Volume Integral

A volume integral, also known as a triple integral, is a mathematical concept used in calculus and vector calculus to calculate the volume of a three-dimensional region within a space. It is an extension of the concept of a definite integral in one dimension to three dimensions.

Mathematically, the volume integral of a scalar function f(x, y, z) over a region R in three-dimensional space is denoted as:

$\bold{\iiint_R f(x, y, z) \ dV}$

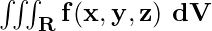
Where

dV represents an infinitesimal volume element, and
Integral is taken over region R.

Operation in Vector

The different operations performed with vector quantities are tabulated below with their notation and illustration.

Operation	Notation	Illustration
Vector Addition	r₁ + r₂	Addition of two vectors gives a vector
Scalar Multiplication	q.r₁	Multiplying a vector ‘r₁‘ with scalar ‘q’ result in a vector
Dot Product	r₁ · r₂	Dot product of two vectors gives a scalar
Cross Product	r₁ ⨯ r₂	Cross product of two vectors gives a vector
Scalar Triple Product	r₁ · (r₂ ⨯ r₃)	Dot Product of Cross product of two vectors
Vector Triple Product	r₁ ⨯ (r₂ ⨯ r₃)	Cross Product of Cross Product of two Vectors

Learn More, Dot and Cross Product of Vectors

Divergence and Curl

Divergence and Curl are two important operators used in Vector Calculus. Divergence is a scalar operator which tells about the behaviour of a function towards or away from a point. Curl is a vector operator which tells about the behaviour of a function around a point. The vector operator is represented by ∇ which accounts for the partial differentiation of the vector field. The Vector Differential Operator (∇) also called Nabla is expressed as ∇ = ∂/∂x i + ∂/∂y j + ∂/∂z k.

Divergence of Vector

If a vector field is given by f(x,y,z) = f_xi + f_yj + f_zk then its divergence is given by taking the scalar of the vector operator is given by

div(f) = ∇.f(x,y,z) = (∂/∂x i + ∂/∂y j + ∂/∂z k) · (f_xi + f_yj + f_zk )

⇒ ∇.f(x,y,z) = ∂_x/∂x + ∂_y/∂y + ∂_z/∂z.

Curl of Vector

If a vector field is given by f(x,y,z) = f_xi + f_yj + f_zk then its curl is given by taking the vector of the vector operator

∇ × f(x,y,z) = (∂/∂x i + ∂/∂y j + ∂/∂z k) ⨯ (f_xi + f_yj + f_zk )

⇒ ∇ × f(x,y,z) = 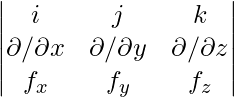$\begin{vmatrix} i & j & k \\ \partial /\partial x& \partial /\partial y & \partial /\partial z \\ f_{x} & f_{y} & f_{z} \\ \end{vmatrix}$

⇒ ∇ × f(x,y,z) = (∂_z/∂y – ∂_y/∂z)i + (∂_x/∂z – ∂_z/∂x)j + (∂_y/∂x – ∂_x/∂y).

Gradient of Scalar

The gradient of a scalar field F is given by grad(F) or ∇ F. It gives the measurement of the rate and direction of a scalar-valued function. In the Cartesian system, the gradient of a scalar-valued function is given by

∇ F = (∂/∂x i + ∂/∂y j + ∂/∂z k)F = ∂/∂x i + ∂/∂y j + ∂/∂z k

Vector Calculus Formulas

For a vector field given as F(x,y,z) = p(x,y,z)i + q(x,y,z)j + r(x,y,z)k. The following formulas are given.

Fundamental Theorem of Line Integral

if F = ∇Φ and Curve C has A and B endpoints then its line integral is given as

∫_cF.dr = Φ(B) – Φ(A)

Circulation Curl Form

There are two theorems under Circulation Curl Form, namely the Green theorem and Stokes theorem.

Green Theorem: If D is the region bounded by curve C then, ∮_cF.dr = ∬_D(∂Q/∂x – ∂P/∂y)dA

Stoke’s Theorem: For a surface S bounded by curve C stokes theorem given by ∮_cF.dr = ∬_S(∇ ⨯ F)dS

Flux Divergence Theorem

The Flux Divergence Form of Green’s Theorem is given as ∬_D∇. F dA = ∮_cF.n ds

The Flux Divergence Form of Stoke’s Theorem is given as ∭_D∇. F dV = ∯_sF.n dσ

Vector Calculus Identities

The list of Vector Calculus Identities have been tabulated under three categories.

Gradient Function Identities

The Gradient Function Identities are tabulated below:

$\vec{\nabla}$ (f + g)	$\vec{\nabla}$ f + $\vec{\nabla}$ g
$\vec{\nabla}$ (cf)	c $\vec{\nabla}$ f, where C is constant
$\vec{\nabla}$ (fg)	f $\vec{\nabla}$ g + g $\vec{\nabla}$ f
$\vec{\nabla}$ (f/g)	(g $\vec{\nabla}$ f – f $\vec{\nabla}g$ )/g2 at point $\vec{x}$ where g( $\vec{x}$ ) ≠ 0
$\vec{\nabla}(\vec{F}+\vec{G})$	$\vec{F} \times(\vec{\nabla} \times \vec{G})-(\vec{\nabla} \times \vec{F}) \times \vec{G}+(\vec{G} \cdot \vec{\nabla}) \vec{F}+(\vec{F} \cdot \vec{\nabla}$

Divergence Function Identities

The identity formula for Divergence Function is tabulated below:

$\vec{\nabla}(\vec{F}+\vec{G})$	$\vec{\nabla} \cdot \vec{F}+\vec{\nabla} \cdot \vec{G}$
$\vec{\nabla} \cdot(c \vec{F})$	$c \vec{\nabla} \cdot \vec{F}$
$\vec{\nabla} \cdot(f \vec{F})$	$f \vec{\nabla} \cdot \vec{F}+\vec{F} \cdot \vec{\nabla}$
$\vec{\nabla} \cdot(\vec{F} \times \vec{G})$	$\vec{G} \cdot(\nabla \times \vec{F})-\vec{F} \cdot(\nabla \times \vec{G})$

Curl Function Identities

The identities for curl function is tabulated below:

$\vec{\nabla} \times(\vec{F}+\vec{G})$	$\nabla \times \vec{F}+\vec{\nabla} \times \vec{G}$
$\vec{\nabla} \times(c \vec{F})$	$c \vec{\nabla} \times \vec{F}$
$\vec{\nabla} \times(f \vec{F})$	$f \vec{\nabla} \times \vec{F}+\vec{\nabla} f \times \vec{F}$
$\vec{\nabla} \times(\vec{F} \times \vec{G})$	$\vec{F} \cdot(\vec{\nabla} \cdot \vec{G})-(\vec{\nabla} \vec{F}) \vec{G}+(\vec{G} \cdot \vec{\nabla}) \vec{F}-(\vec{F} \cdot \vec{\nabla})$

Laplacian Function Identities

The identities for Laplacian Function is tabulated below:

$\vec{\nabla}^2(f+g)$	$\vec{\nabla}^2 f+\vec{\nabla}^2 g$
$\vec{\nabla}^2(c f)$	$c \vec{\nabla}^2 f$ , where C is a constant
$\vec{\nabla}^2(f g)$	$f \vec{\nabla}^2 g+2 \vec{\nabla} f \cdot g+g \vec{\nabla}^2$

Degree Two Function Identities

The vector calculus identities for two degree function is tabulated below:

$\vec{\nabla} \cdot(\nabla \times \vec{F})$	0
$\vec{\nabla} \times(\vec{\nabla} f)$	0
$\vec{\nabla} \cdot(\overrightarrow{\nabla f} \times \overrightarrow{\nabla g})$	0
$\vec{\nabla} \cdot(f \overrightarrow{\nabla g}-g \vec{\nabla})$	$f \vec{\nabla}^2 g-g \vec{\nabla}^2 f$
$\vec{\nabla} \times(\nabla \times \vec{F})$	$\vec{\nabla}(\vec{\nabla} \cdot \vec{F})-\vec{\nabla}^2$

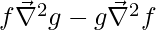
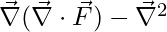
Vector Calculus Applications

Vector Calculus or vector analysis has a number of applications in the real world:

Navigation
Sports
Partial differential equation
Three-dimensional geometry
Used in heat transfer

Related Resources,

Implicit Differentiation in Calculus
How to find Derivatives?
Vector Algebra

Solved Examples on Vector Calculus

Example 1: If F(x,y,z) = 3xy² – y²z³ then find gradF or ∇ f.

Solution:

∇ f = (∂/∂x i + ∂/∂y j + ∂/∂z k)(3xy² – y²z³)

⇒ ∇ f = ∂/∂x(3xy² – y²z³)i + ∂/∂y(3xy² – y²z³)j + ∂/∂z (3xy² – y²z³)k

⇒ ∇ f = 3y²i + (6xy – 2yz³) + (-3y²z²)k

Example 2: Find the div(F) or ∇·F, if F = xz²i – 2y²z³j + x²yz k

Solution:

div(F) = ∇·F = (∂/∂x i + ∂/∂y j + ∂/∂z k)·(xz2 i – 2y2z3 j + x2yz k)

⇒ ∇·F = ∂/∂x(xz2) + ∂/∂y(- 2y2z3) + ∂/∂z(x2yz)

⇒ ∇·F = z² – 4yz³ + x²y

Example 3: Find curl F i.e. ∇ × f if F = xz² i – 2x³yz j + 2yz⁴ k

Solution:

∇ × f= (∂/∂x i + ∂/∂y j + ∂/∂z k) ⨯ (xz² i – 2x³yz j + 2yz⁴ k)

⇒ ∇ × f = 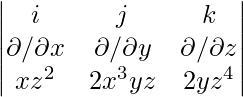$\begin{vmatrix} i & j & k \\ \partial /\partial x& \partial /\partial y & \partial /\partial z \\ xz^{2} & 2x^{3}yz & 2yz^{4} \\ \end{vmatrix}$

⇒ ∇ × f = [∂/∂y(2yz⁴) – ∂/∂z(-2x³yz)]i + [∂/∂z(xz²) – ∂/∂x(2yz⁴)]j + [∂/∂x(-2x³yz) – ∂/∂y(xz²)]k

⇒ ∇ × f = [2z⁴ + 2x³y]i + [2xz – 0]j + [-6x²yz – 0]k

⇒ ∇ × f = (2z⁴ + 2x³y)i + (2xz)j -(6x²yz)k

FAQs on Vector Calculus

1. What is Vector Calculus?

Vector Calculus is branch of mathematics that deals with the differentiation and integration of Vector Function.

2. What is Gradient in Vector Calculus?

Gradient in Vector Calculus is rate of change of a scalar valued function in a vector space.

3. What is Divergence in Vector Calculus?

Divergence in Vector Calculus is the scalar of the vector operation of a function.

4. What is Curl in Vector Calculus?

Curl in Vector Calculus is vector of vector operation of a function.

5. What is Line Integral?

Line integral is the integration of the function along the lines of the curve.

6. What is Surface Integral?

Surface Integral of the function is the integration of the function over the whole surface.

7. Who invented Vector Calculus?

The concept of Vector Calculus was given by J. Willard Gibbs and Oliver Heaviside.

8. is Vector Calculus same as vector analysis?

Yes, Vector Calculus is also called vector analysis.

Suggest improvement

Homogeneous Differential Equations

Share your thoughts in the comments

Limits

Continuity and Differentiability

Derivatives

Derivatives of Various Functions

Advanced Differentiation

Application of Derivatives

Integrals

Indefinite Integration

Definite Integration

Application of Integration

Differential Equation

Vector Calculus in Maths

What is Vector Calculus?

Vector Calculus Definition

Line Integral

Surface Integral

Volume Integral

Operation in Vector

Divergence and Curl

Divergence of Vector

Curl of Vector

Gradient of Scalar

Vector Calculus Formulas

Fundamental Theorem of Line Integral

Circulation Curl Form

Flux Divergence Theorem

Vector Calculus Identities

Gradient Function Identities

Divergence Function Identities

Curl Function Identities

Laplacian Function Identities

Degree Two Function Identities

Vector Calculus Applications

Solved Examples on Vector Calculus

FAQs on Vector Calculus

1. What is Vector Calculus?

2. What is Gradient in Vector Calculus?

3. What is Divergence in Vector Calculus?

4. What is Curl in Vector Calculus?

5. What is Line Integral?

6. What is Surface Integral?

7. Who invented Vector Calculus?

8. is Vector Calculus same as vector analysis?

Please Login to comment...

Similar Reads

What kind of Experience do you want to share?