L’ Hospital Rule in Calculus: L’Hospital Rule is one of the most frequently used tools in entire calculus, which helps us calculate the limit of those functions that seem indeterminate forms. For many years, these indeterminate forms have been considered impossible to solve for function but some scholars found out that some functions have limits which can be seen in the graph but the calculation seems to result in an indeterminate form. Hence, the L’hospital rule is born.
In this article, we will learn about the concept of the L’Hospital Rule in detail. Other than that, this article also covers indeterminate forms, the L’Hospital Rule formula, and proof of the L’Hospital Rule formula with examples as well.
What is L’Hospital Rule in Calculus?
L’Hospital rule states that when the limit is applied to a fraction of two functions resulting in an indeterminate form then it is equal to the limit of the fraction formed by the individual derivatives of functions. The L’Hospital rule uses derivatives of each function to solve the limit which helps us evaluate the limits which results in an indeterminate form.
L’Hospital Rule Definition
L’Hôpital’s Rule, named after the French mathematician Guillaume de l’Hôpital, is a mathematical theorem used to evaluate limits of indeterminate forms.
The indeterminate forms are the forms with two functions whose limits cannot be determined by putting the limits in the function. The indeterminate form is the form that is undefined mathematically. The forms whose value cannot be evaluated by directly applying the limits are called indeterminate forms. Indeterminate form includes 0/0, ±∞/±∞, 0×∞, ∞-∞, 00, 1∞ etc. The 0/0, and ±∞/±∞ are the most common indeterminate forms in which the L’Hospital rule is applied.
For two continuous and differentiable functions f(x) and g(x) if limits x tends to result in an indeterminate form, then the L’Hospital rule is applied and it states,
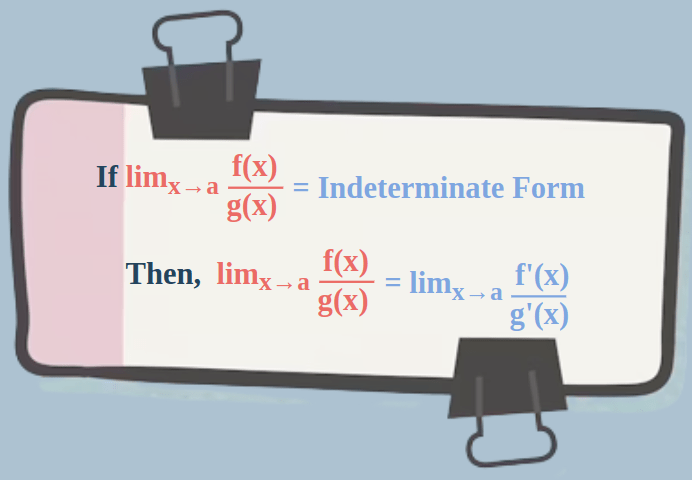
Where,
- a is any real number or infinity.
- f'(x) is derivative of f(x)
- g'(x) is derivative of g(x) and g(x) and g(a) ≠ 0
When to use L’Hospital Rule
The L’Hospital rule is used when the limits of two differentiable functions after applying the limit gives an indeterminate form. Commonly, for the indeterminate forms 0/0, ±∞/±∞ we apply the L’Hospital rule directly to evaluate the limit.
Conditions for L’Hospital Rule
Some necessary conditions for applying the L’Hospital rule
- f(x) and g(x) must be differentiable.
- The limit of the quotient of the derivatives of a given function should exist i.e.,
limx→a f'(x) / g'(x) = Some Finite Number
L’Hospital Rule Proof
The L’Hospital rule is applied when limits result in indeterminate form 0/0, ±∞/±∞. We can prove the L’Hospital rule by using Cauchy’s Mean Value Theorem.
Let f(x) and g(x) be two continuous functions on the interval [a, b] and differentiable on the interval (a, b) and we know for any function f(x), its derivative at x = c is given as
f'(c) = [f(x) – f(c)]/(x – c)
Assume that g(x) = 0 on (a, b), then there exists c in (a, b) such that
lim x→b [f'(x) / g'(x)] = lim x→b [{(f(x)- f(b)) / (x – b)} / {(g(x)- g(b)) / (x – b)}]
Let the functions f and g be differentiable at x = c satisfying where c belongs to the interval in which functions are defined. Let f(c) = g(c) = 0.
By Cauchy’s Mean Value Theorem,
limx→c [f(x) / g(x)] = lim x→c[f(x) -f(c)]/[g(x) – g(c)]
⇒ lim x→c [f(x) / g(x)] = lim x→c[f(x) – 0] / [g(x) – 0] {as f(c) = g(c) = 0}
⇒ lim x→c [f(x) / g(x)] = lim x→c[f(x) – f(c)] / [g(x) – g(c)]
⇒ limx→c [f(x) / g(x)] = lim x→c [{(f(x)- f(c)) / (x – c)} / {(g(x)- g(c)) / (x – c)}]
⇒ limx→c [f(x) / g(x)] = limx→c [f'(x) / g'(x)]
Which is the required result.
Learn more about Mean Value Theorem.
How to Apply L’Hospital Rule?
L’Hospital rule is applied when we get an indeterminate form after applying the limits. For applying the L’Hospital Rule these are the following steps:
- First check after applying the limit we get indeterminate form or not. If we do not get indeterminate form then, we cannot apply L’Hospital rule.
- When we get indeterminate form, simplify the fraction before applying the rule.
- Find the derivatives of the functions separately.
- Determine the value of ratio of derivatives to get the result.
Example: Find limx→1 [(x10 – 1) / (x2 – 1)]
Solution:
First apply the limit
limx→1 [(x10 – 1) / (x2 – 1)] = [110 -1] / [12 -1] = 0 / 0
After applying the limit, we get 0 / 0 form so, we apply L’Hospital rule
f(x) = x10 – 1
⇒ f'(x) = 10x9
g(x) = x2 – 1
⇒ g'(x) = 2x
limx→1 [(x10 – 1) / (x2 – 1)] = (10x9) / 2x
Now, put limit x = 1, we get
⇒ limx→1 [(x10 – 1) / (x2 – 1)] = [(10×19 )-1] / [2×1] = 10 / 2
⇒ limx→1 [(x10 – 1) / (x2 – 1)] = 5
Applying L’Hospital Rule Multiple Times
When the L’Hospital rule is applied once and also after applying the limit we get an indeterminate form then after simplifying the fraction, we can again apply L’Hospital Rule. We can apply the rule multiple times until we get an indeterminate form. Before each application of the L’Hospital rule, we should simplify the fractions.
Example: Find limx→0 [(sinx – x) / x2]
Solution:
First apply the limit
limx→0 [(sinx – x) / x2] = (sin0 – 0) / 02 = 0/0
After applying the limit, we get 0 / 0 form so, we apply L’Hospital rule
f(x) = sin x – x
⇒ f'(x) = cos x -1
g(x) = x2
⇒ g'(x) = 2×0
limx→0 [(sinx – x) / x2] = (cos x -1) / 2x
Now, put limit x = 0, we get
limx→0 [(sinx – x) / x2] = (cos 0 -1) / 2×0 = 0 / 0
Again we get 0 / 0 form so, we again apply L’Hospital rule
f(x) = cos x – 1
⇒ f'(x) = -sinx
g(x) = 2x
⇒ g'(x) = 2
limx→0 [(sinx – x) / x2] = (-sin x) / 2
Now, put limit x = 0, we get
limx→0 [(sinx – x) / x2] = (- sin 0) / 2 = 0
⇒ limx→0 [(sinx – x) / x2] = 0
How to apply L’Hospital Rule for Exponents
When the variable is in power, we equate the limit with a variable and take the logarithm on both sides and then apply the L’Hospital rule.
Example: Evaluate: limx→∞ x1/x
Solution:
The given limit gives ∞0
In this question we have variable in the exponent, so we take ln
y = x1/x
Taking ln both sides in the above equation.
ln y = ln x1/x
⇒ ln y = (1 / x) ln x
Applying limit
limx→∞ ln y = limx→∞ (1 / x) × ln x
⇒ limx→∞ ln y = limx→∞ (ln x) / x
Applying L’Hospital rule
limx→∞ ln y = limx→∞ (1 / x) / 1
⇒ limx→∞ ln y = limx→∞ (1 / x)
putting limit
limx→∞ ln y = 1 / ∞ = 0
⇒ ln [limx→∞ y] = 0
⇒ limx→∞ y = e0
⇒ limx→∞ y = 1
⇒ limx→∞ x1/x = 1
Key Points about L’ Hospital Rule
Some of the key points which we need to remember related to L’Hospital’s rule are:
- If the limit does not result in an indeterminate form after applying the limit, then we cannot apply the L’Hospital rule (it provides an incorrect result).
- Each time before applying the rule, we should simplify the rational expression.
- If the limit is given in product form like f(x). g(x) then, for applying the rule we can rewrite it as f(x) / 1 / g(x) or g(x) / 1 / f(x).
- While applying the L’Hospital rule multiple times always check if the resulting rational expression gives an indeterminate form or not.
People Also Read:
L’Hospital Rule Examples with Solutions
Problem 1: Find limx→-2 [(x + 2) / (x2 + 3x + 2)]
Solution:
First apply the limit
limx→-2 [(x + 2) / (x2 + 3x + 2)] = limx→-2 [(- 2 + 2) / ((-2)2 + 3×(-2) + 2)] = 0 / 0
After applying the limit, we get 0 / 0 form so, we apply L’Hospital rule
f(x) = x + 2
⇒ f'(x) = 1
g(x) = x2 + 3x + 2
⇒ g'(x) = 2x + 3
limx→-2 [(x + 2) / (x2 + 3x + 2)] = 1 / (2x + 3)
Now, put limit x = -2, we get
limx→-2 [(x + 2) / (x2 + 3x + 2)] = 1 / [2×(-2) + 3] = 1 / (-4 + 3)
⇒ limx→-2 [(x + 2) / (x2 + 3x + 2)] = -1
Problem 2: Find limx→0 [sin 3x / x]
Solution:
First apply the limit
limx→0 [sin 3x / x] = sin 3(0) / 0 = 0 / 0
After applying the limit, we get 0 / 0 form so, we apply L’Hospital rule
f(x) = sin3x
⇒ f'(x) = 3cos3x
g(x) = x
⇒ g'(x) = 1
limx→0 [sin 3x / x] = 3cos 3x / 1
Now, put limit x = 0, we get
limx→0 [sin 3x / x] = [3cos 3(0)] / 1 = 3 / 1
⇒ limx→0 [sin 3x / x] = 3
Problem 3: Find limx→∞ [x2 / ex]
Solution:
First apply the limit
limx→∞ [x2 / ex] = ∞2 / e ∞ = ∞ / ∞
After applying the limit, we get ∞ / ∞ form so, we apply L’Hospital rule
f(x) = x2
⇒ f'(x) = 2x
g(x) = ex
⇒ g'(x) = ex
⇒ limx→∞ [x2 / ex] = 2x / ex
Now, put limit x = ∞, we get
limx→∞ [x2 / ex] = (2 × ∞)/ e∞ = ∞ / ∞
Again we get ∞ / ∞ form so, we again apply L’Hospital rule
f(x) = 2x
⇒ f'(x) = x
g(x) = ex
⇒ g'(x) = ex
limx→∞ [x2 / ex] = 2 / ex
Now, put limit x = ∞, we get
limx→∞ [x2 / ex] = 2 / ex = 2 / e∞ = 2 / ∞
⇒ limx→∞ [x2 / ex] = 0
Problem 4: Evaluate: limx→∞ xx
Solution:
The given limit gives ∞∞
In this question we have variable in the exponent, so we take ln
y = xx
Taking ln
ln y = ln xx
⇒ ln y = x ln x
Applying Limit
limx→∞ ln y = limx→∞ xlnx
⇒ limx→∞ ln y = limx→∞ [lnx / ( 1 / x)]
Applying L’Hospital rule
limx→∞ ln y = limx→∞ [(1 / x) / ( -1 / x2)]
⇒ limx→∞ ln y = limx→∞ [-(1 / x) / (1 / x)2]
⇒ limx→∞ ln y = limx→∞ [-1 / (1 / x)]
⇒ limx→∞ ln y = limx→∞ (-x)
putting limit
limx→∞ ln y = -∞
⇒ ln limx→∞ y = -∞
⇒ limx→∞ y = e-∞
⇒ limx→∞ y = 0
⇒ limx→∞ xx = 0
Practice Problems on L’Hospital Rule
Find the following limits.
- [Tex]\lim_{{x \to 2}} \frac{{x^2 – 4}}{{x – 2}}
[/Tex]
- [Tex]\lim_{{x \to 0}} \frac{{e^x – 1}}{{x}}
[/Tex]
- [Tex]\lim_{{x \to \infty}} \frac{{x^2 + 3x}}{{2x^2 – 5}}
[/Tex]
- [Tex]\lim_{{x \to \infty}} \frac{{\ln(x)}}{{x}}
[/Tex]
- [Tex]\lim_{{x \to 0}} \frac{{\sin(x)}}{{x}}
[/Tex]
- [Tex]\lim_{{x \to 0}} \frac{{1 – \cos(x)}}{{x^2}}
[/Tex]
- [Tex]\lim_{{x \to \infty}} \left(1 + \frac{2}{x}\right)^x
[/Tex]
- [Tex]\lim_{{x \to \infty}} \left(\frac{{x + 1}}{{x}}\right)^{3x}
[/Tex]
FAQs on L’Hospital Rule in Calculus
What is L’Hospital Rule?
L’Hospital rule states that when the limit is applied to ratio of two differentiable functions whose value after putting the limit results in indeterminate form is equal to the limit of the ratio of each function’s derivatives.
If limx→a [f(x) / g(x)] = Indeterminate form, L’Hospital Rule Formula is given by:
limx→a [f(x) / g(x)] = limx→a [f'(x) / g'(x)]
Where,
- a is any real number or infinity,
- f'(x) is derivative of f(x), and
- g'(x) is derivative of g(x) and g(x) and g(a) ≠ 0.
When we apply L’Hospital Rule?
When for the given limits after applying the limit, we get indeterminate form (mostly 0/0, ±∞/±∞) and both functions are differentiable then, we apply L’Hospital rule.
Can L’Hospital Rule be applied multiple times?
Yes, L’Hospital rule can be applied multiple times if the resultant fraction gives indeterminate form again and again.
Indeterminate forms are the forms with the ratio of two functions whose value in indeterminate after applying the limits. Some of the indeterminate forms are: 0/0, ±∞/±∞, 0×∞, ∞-∞, 00, 1∞ .
What are the Limitations of L’Hospital’s Rule?
One of the major limitations of L’Hospital’s Rule is that it can only be applied for indeterminate forms of either 0/0 or (+/-infinity)/(+/-infinity). All the other forms first need to be converted into these forms if possible.
Share your thoughts in the comments
Please Login to comment...