Standard Form of a Straight Line

There are several forms are available to represent the equation of a straight line on the 2-dimensional coordinate plane, out of several forms three major forms are point-slope form, slope-intercept form, and general or standard form. General or standard form is a linear equation where the degree of the equation is one.

Standard form equation

The equation of standard form is

Ax + By + C = 0

Ax + By = C

Here, A, B, and C are the real constant and the value of A and B is not zero simultaneously. So, we can say that an equation of Ax + By + C = 0 form where A and B is not zero simultaneously is known as the general equation of standard equation of a line. The graph of a standard equation is always straight.

If the value of A = 0 then the equation of the line is y = -C/B and the line is horizontal, means parallel to x-axis and if the value of B = 0, then the equation of the line is x = -C/A and the line is vertical, means parallel to y-axis.

For example:

2x + 4y + 3 = 0
4x – 6y = -34
Both the equations are in the standard form
3x = -3y – 2
3y = 2(x + 1)
Both the given equations are not in the standard form

Types of standard form

The standard form of the equation can of represented into three different forms:

Slope-Intercept form: As we know that the equation of slope-intercept form is y = mx + c. Now we see how to represent the general equation i.e., Ax + By + C = 0 in the Slope-intercept form.

So, if the value of B ≠ 0, then the general equation i.e., Ax + By + C = 0 can be written as:

$y = -\frac{A}{B}-\frac{C}{B}$ -(1)

Now, compare the equation(1) with the slope intercept form,i.e. y = mx + c, we get

m = -A/B, and c = -C/B

Hence, the slope of the Ax + By + C = 0 is -A/B and the y-intercept is -C/B.

Examples:

Question 1. Find the slope and the y-intercept of the given equation, 2x + 5y + 1 = 0.

Solution:

Given: equation of line = 2x + 5y + 1 = 0
Find: slope and y-intercept
So the given equation can be written as
y = (-1 – 2x)/5
y = -2x/5 – 1/5 -(1)
As we know that the slope-intercept form is
y = mx + c -(2)
On comparing eq(1) and (2) we get
m = -2/5 and c = -1/5
Hence, the slope is -2/5 and y-intercept is -1/5

Question 2. Find the slope and the y-intercept of the given equation, 3x + 6y – 9 = 0.

Solution:

Given: equation of line = 3x + 6y – 9 = 0
Find: slope and y-intercept
So the given equation can be written as
y = (9 – 6x)/3
y = -2x + 3 -(1)
As we know that the slope-intercept form is
y = mx + c -(2)
On comparing eq(1) and (2) we get
m = -2 and c = 3
Hence, the slope is -2 and y-intercept is 3

Intercept Form: As we know that the intercept form of the equation is 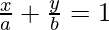$\frac{x}{a}+\frac{y}{b}=1$ . Now we see how to represent the general equation i.e., Ax + By + C = 0 in the intercept form.

So, if the value of C ≠ 0, then the general equation i.e., Ax + By + C = 0 can be represented as:

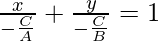$\frac{x}{-\frac{C}{A}}+\frac{y}{-\frac{C}{B}} = 1$ -(1)

Now, compare the equation(1) with the intercept form,i.e. 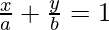$\frac{x}{a}+\frac{y}{b}=1$ , we get

a = -C/A and b = -C/B

So, the x-intercept is -C/A and y-intercept is -C/B. And if the value of C = 0, then the general equation is Ax + By = 0, means the line is pass through origin so, it has zero intercept.

Examples:

Question 1. Find the x and y-intercept of the given equation, 4x + 8y + 2 = 0.

Solution:

Given: 4x + 8y + 2 = 0.
Find: x and y-intercept
So the given equation can be written as
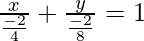$\frac{x}{\frac{-2}{4}}+\frac{y}{\frac{-2}{8}}=1$ -(1)
As we know that the Intercept Form is
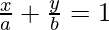$\frac{x}{a}+\frac{y}{b}=1$ -(2)
On comparing eq(1) and (2) we get
a = -2/4 = -1/2
b = -2/8 = -1/4
So the x-intercept is -1/2 and y-intercept is -1/4

Question 2. Find the x and y-intercept of the given equation, 12x – 4y – 2 = 0.

Solution:

Given: 12x – 4y – 2 = 0
Find: x and y-intercept
So the given equation can be written as
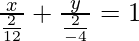$\frac{x}{\frac{2}{12}}+\frac{y}{\frac{2}{-4}}=1$ -(1)
As we know that the Intercept Form is
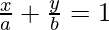$\frac{x}{a}+\frac{y}{b}=1$ -(2)
On comparing eq(1) and (2) we get
a = 2/12 = 1/6
b = -2/4 = -1/2
So the x-intercept is 1/6 and y-intercept is -1/2

Normal Form: As we know that the intercept form of the equation is xcosω + ysinω = p. Now we see how to represent the general equation i.e., Ax + By + C = 0 in the normal form.

So let us considered the normal form is xcosω + ysinω = p of the line represented by the equation Ax + By + C = 0.

So, 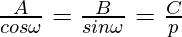$\frac{A}{cos\omega} = \frac{B}{sin\omega} = \frac{C}{p}$

cosω = -Ap/C and sinω = -Bp/C

As we know that

sin²ω + cos²ω = 1 -(1)

So put all these value in equation (1), we get

(-Ap/C)²+ (-Bp/C)²= 1

$p^2 = \frac{C^2}{A^2 +B^2}$

$p = \frac{C}{\sqrt{A^2 + B^2}}$

So, $cos\omega = \frac{A}{\sqrt{A^2 + B^2}} \ and \ sin\omega =\frac{B}{\sqrt{A^2 + B^2}}$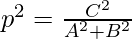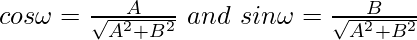

So, the normal form of the general equation is xcosω + ysinω = p.

Examples:

Question 1. Convert the given equation in the normal form 2x – 2y – 6 = 0.

Solution:

Given: 2x – 2y – 6 = 0
Divide the given equation
√(2)² + (-2)² = √4 + 4 = √8 = 2√2
So, 2x/2√2 – 2y/2√2 = 6/2√2
x/√2 – y/√2 = 3/√2 (1)
As we know that the Intercept Form is
xcosω + ysinω = p -(2)
On comparing eq(1) and (2) we get
cosω = 1/√2
sinω = -1/√2
So, xcos45° + ysin225° = 3/√2

Question 2. Find the value of p and ω, equation is x + y + 3 = 0.

Solution:

Given: x + y + 3 = 0
Divide the given equation
√(1)² + (1)² = √2
So, x/√2 + y/√2 = -3/√2 (1)
As we know that the Intercept Form is
xcosω + ysinω = p -(2)
On comparing eq(1) and (2) we get
cosω = 1/√2
sinω = 1/√2
xcos45° + ysin45° = -3/√2
Hence, p = -3/√2 and ω = 45°

Graphing a linear equation: 5x + 2y = 20

To create a graph of the linear equation 5x + 2y = 20. We need to find the coordinates of the x-axis and y-axis.

Step 1: So, we solve for y:

5x + 2y = 20 -(1)

Subtract -5x on both side

5x – 5x + 2y = 20 – 5x

2y = 20 – 5x -(2)

Now divide equation (2) by 2, we get

2/2y = (20 – 5x)/2

y = 10 – 5x/2 -(3)

Now, we arrange equation(3) to the slope intercept form, i.e., y = mx + b

y = -5x/2 + 10

Now, the slope of the equation(m) is -5/2 and y-intercept(b) is 10.

Step 2: Now we create a table to find the points:

x	y = 10 – 5x/2	Points
0	y = 10-5(0)/2	(0, 10)
2	y = 10 – 5(2)/2	(2, 5)
4	y = 10 – 5(4)/2	(4, 0)

Step 3: After finding points, draw x-axis and y-axis on the graph and plot all these coordinates on the graph.

Step 4: Now draw a straight line by joining the points, here this straight line represents the given linear equation.

How to convert slope-intercept to standard form?

Let us discuss how to convert slope-intercept to standard form with the help of an example.

We have an equation y = 3/5x + 2/9. Now we convert the given equation into the standard form. Here, the given equation is written in slope-intercept form, i.e., y = mx + c, and we have to convert the given equation in standard form that is Ax + By + C = 0.

So, the given equation is multiplied by 45 on both sides, because 45 is divisible by 5 and 9

45y = 45(3x/5) + 45(2/9)

45y = 9(3x) + 5(2)

45y = 21x + 10

or 21x – 45y + 10 = 0

So, the standard form of the equation y = 3/5x + 2/9 is 21x – 45y + 10 = 0.

Last Updated : 05 Nov, 2021