A Harmonic Progression (H.P.) is a mathematical sequence generated by taking the reciprocals of an Arithmetic Progression. In this sequence, each term is the harmonic mean of its adjacent terms, this series is called Harmonic Progression.
A Harmonic Progression of separate unit fractions cannot add to an integer (unless in the specific case where (a = 1 and d = 0). The reason lies in the fact that the progression will contain at least one denominator divisible by a prime number that does not a divisor of any other denominator. Harmonic Progression is also called Harmonic Sequence.
In this article, we will discuss the definition, applications, and formula of Harmonic Progression, and understand the difference and relation between arithmetic mean, geometric mean, and harmonic mean to calculate Harmonic Progression in mathematics.
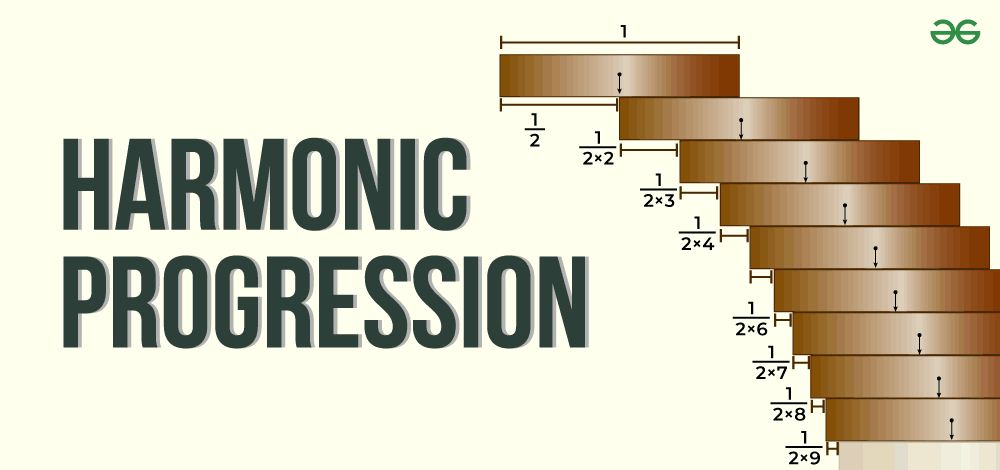
What is Harmonic Progression (HP)?
The Harmonic Progression is derived by taking the reciprocals of the terms in an Arithmetic Progression. If the Arithmetic Progression is represented by the terms a, a + d, a + 2d, a + 3d, and so on, then the corresponding terms in the Harmonic Progression (or Harmonic sequence) are 1/a, 1/(a + d), 1/(a + 2d), 1/(a + 3d), 1/(a + 4d), and so forth up to 1/(a + (n – 1)d). In this context, ‘a’ stands for the initial term and ‘d’ is the common difference, both of which are non-zero values.
Harmonic Progression Definition
A Harmonic Progression (HP) is defined as a sequence of real numbers obtained by taking the reciprocals of an Arithmetic Progression that excludes 0. In this progression, each term is calculated as the Harmonic Mean of its two adjacent terms. For example, if we have a sequence like a, b, c, d, … forming an Arithmetic Progression, the corresponding Harmonic Progression is represented as 1/a, 1/b, 1/c, 1/d, …
Harmonic Progression Example
There are infinitely many examples of Harmonic Progression. Some of the examples of Harmonic Progression are mentioned below:
- Harmonic Progression of Natural Numbers: 1/1, 1/2, 1/3, 1/4…..
- Leaning Tower of Lire: 1/2, 1/4, 1/6, 1/8, 1/10,…..
Some Other Examples of Harmonic Progression are mentioned below:
- 1/3, 1/5, 1/7, 1/9….
- 1/4, 1/8, 1/12, 1/16….
- 1/5, 1/10, 1/15, 1/20….
When expressing the Arithmetic Progression in the format a, a+d, a+2d, a+3d, …, a+(n−1)d, the formula for the Harmonic Progression can be stated as follows: 1/a, 1/(a+d), 1/(a+2d), 1/(a+3d), and so on. The initial term is denoted by ‘a’ and the common difference by ‘d’.
In order to approach Harmonic Progression problems, the first step involves calculating the sum of the corresponding Arithmetic Progression. This calculation says that the nth term in the Harmonic Progression is the reciprocal of the nth term in the analogous Arithmetic Progression.
The general term (an) or nth term of the Harmonic Progression (H.P.) is given by the formula
an = 1 / [a + (n – 1)d]
Where
- “a” represents the initial term of the Harmonic Progression (H.P.)
- “d” stands for the common difference between successive terms,
- “n” denotes the total number of terms in the Harmonic Progression (H.P.)
Harmonic Progression Sum
An Arithmetic Progression (AP), also known as an Arithmetic sequence, is a set of numbers characterized by a constant difference between successive terms. On the other hand, a Harmonic Progression (HP) or Harmonic Sequence is generated by taking the reciprocals of an Arithmetic Progression.
Creating a Harmonic Progression or 1/AP is a straightforward process. Using the formula for the nth term in an Arithmetic Progression, a + (n-1)d, we can quickly generate the Harmonic Progression sequence.
However, calculating the sum of this progression can be tedious. One approach involves either iterating through the sequence or employing approximations to create a formula that provides an accurate value up to a few decimal places.
To find the Sum of n terms in a Harmonic Progression (Sn) for the sequence 1/a, 1/a+d, 1/a+2d, …, 1/a+(n−1)d, the formula is:
Sn= 1/d.ln{2a+(2n−1)d}/(2a − d)}
where,
- “a” denotes the first term of the Harmonic Progression (H.P.)
- “d” represents the common difference in the Harmonic Progression (H.P.)
- “ln” stands for the natural logarithm.
What is Harmonic Sequence?
A Sequence is classified as a Harmonic Sequence when the reciprocals of its elements or numbers create an Arithmetic Sequence.
In a Harmonic Sequence, the progression takes the form of reciprocals: 1/a1, 1/a2, 1/a3, …, 1/an.
For Example, consider the Harmonic Sequence: 1/3, 1/6, 1/9, 1/12, 1/15.
- In this example, the reciprocals of the terms yield an Arithmetic sequence: 3, 6, 9, 12, 15.
- Also, if the sequence a, b, c, d, … is assumed to be an Arithmetic sequence,
- Then the corresponding Harmonic Sequence will be expressed as : 1/a, 1/b, 1/c, 1/d, …
Harmonic Mean
In a harmonic progression, any term of the series is the harmonic mean of its neighboring terms. Harmonic Mean = n /[1/a + 1/(a + d)+ 1/(a + 2d) +1/(a + 3d) +….] Harmonic mean of two terms a and b = (2ab) / (a + b). Harmonic mean of three terms a, b, and c = (3abc) / (ab + bc + ca). The Harmonic Mean is computed as the reciprocal of the Arithmetic Mean of the reciprocals.
To calculate the Harmonic Mean, you can use the formula:
Harmonic Mean = n /[1/a + 1/(a + d) + 1/(a + 2d) + 1/(a + 3d) + ….]
Where
- a is initial value
- d is common difference,
- n is number of terms in the sequence.
The Harmonic Mean between two terms, a and b, can be determined using the formula:
Harmonic Mean between Two Terms = (2ab) / (a + b)
Similarly, the Harmonic Mean for three terms, a, b, and c, is calculated by
Harmonic Mean for Three terms = (3abc) / (ab + bc + ca)
Where a, d, and n represent the values and the number of values present.
Arithmetic Mean (AM), Geometric Mean (GM) and Harmonic Mean (HM)
To know the relation between the AM, GM and HM, we need the formulas of all these three types of mean.
Suppose that “r” and “s” are the two numbers and the number of values = 2, then
AM = (r+s)/2
⇒ 1/AM = 2/(r+s) ……. (1)
GM = √(rs)
Taking square both side
⇒GM2 = rs ……. (2)
HM= 2/[(1/r) + (1/s)]
⇒ HM = 2/[(r+s)/rs]
⇒ HM = 2rs/(r+s) ….. (3)
Now, put (1) and (2) in (3), we get
HM = GM2 /AM
⇒GM2 = AM × HM
GM = √[ AM × HM]
Hence, the relation between AM, GM and HM is
GM2 = AM × HM
Therefore the square of the Geometric Mean is equal to the product of the Arithmetic Mean and the Harmonic Mean.
Read More:
Applications of Harmonic Progression
Harmonic progression finds significant applications in various domains. Some of its applications are listed below:
- Scientific Experimentation Precision: Scientists utilize harmonic formulae to determine experiment values accurately.
- Boiling Point Variation in Water: Harmonic progression aids in understanding how the boiling point of water changes with consistent alterations in temperature.
- Musical Notes: The concept of harmonic sequence is fundamental in music theory, particularly in understanding musical notes.
- Rainfall Estimation and Weather: Harmonic progression is employed to estimate rainfall, the concept’s applicability in weather forecasting and related domains.
- Traffic Flow Analysis: Real-life traffic patterns, such as traffic bunching, can be modeled using harmonic sequences, offering insights for traffic management.
- Geometry and Spatial Relations: In geometry, harmonic progression is used to describe harmonic conjugates and their relationships among collinear points.
- Altitudes and Side Relations in Triangles: Harmonic progression is utilized to establish relationships between altitudes and sides in triangles.
- Business Planning and Predictions: Harmonic progression plays a crucial role in aiding businesses in activities like financial budgeting, sales predictions, and weather forecasts, enabling efficient planning and predictions.
- Electrical Engineering and Power Generation: Concepts of harmonics are fundamental in the field of electrical engineering, particularly in electrical gadgets, machines, and power generation.
People Also View:
Solved Examples on Harmonic Progression
Example 1: Find the value of the 21st term and the nth term of the Harmonic Progression: 1/5, 1/9, 1/13, 1/14 …..?
Solution:
Given the Harmonic sequence: 1/5, 1/9, 1/13, 1/14, …
Comparing this with the general Harmonic sequence formula 1/a, 1/(a + d), 1/(a + 2d), … leads to the identification of the initial terms: 1/a = 1/5 and 1/(a + d) = 1/9.
By solving for ‘a’ and ‘d’, we find that a = 5 and d = 4.
To determine the 21st term, we utilize the formula for the nth term in a Harmonic sequence: 1/(a + (n – 1)d).
The 21st term = 1/(a + 20d) = 1/(5 + 20 x 4) = 1/(5 + 80) = 1/85.
The nth term = 1/(a + (n – 1)d) = 1/(5 + (n – 1)4) = 1/(5 + 4n – 4) = 1/(4n + 1)
Therefore, the 21st term is 1/85, and the nth term is 1/(4n + 1).
Example 2: Determine the 12th term of the Harmonic Progression, if the fifth term is 1/16, and the eighth term is 1/25.
Solution:
Given;
The Fifth term = 1/(a + 4d) = 1/16
The Eight term = 1/(a + 7d) = 1/25
Comparing this with the general Harmonic sequence formula we have a + 4d = 16, and a + 7d = 25.
By solving for ‘a’ and ‘d’, we find that a = 4 and d = 3.
The 12th term of the Harmonic Progression = 1/(a + 11d) = 1/(4 + 11×3) = 1/(4 + 33) = 1/37.
Therefore, the 12th term of the harmonic progression is 1/37.
Example 3: Calculate the 16th term of Harmonic Progession if the 6th and 11th term of Harmonic Progession are 10 and 18, respectively.
Solution:
The Harmonic ProgessionH is written in terms of A.P
We equate the sixth term of the A.P. to a+5d = 1/10
And the eleventh term to a+10d = 1/18
Solving these equations we get, a =13/90, and d = -2/ 225
To determine the 16th term, we use the expression
a+15d = (13/90) – (2/15) = 1/90
Thus the 16th term of the Harmonic Progression equates to the 1/16th term of the Arithmetic Progression (A.P.), which equals 90.
Harmonic Progression Questions
Q1. The second and the fifth term of the Harmonic Progression is 3/14 and 1/10. Calculate the sum of 6th and 7th term of the series.
Q2. The sum of the reciprocals of the first 12 terms in the Harmonic Progression series is 110. Determine the 8 terms of the Harmonic Progression series.
Q3. Determine the 6th and 10th term of the Harmonic Progression 6, 4, 3,…
Q4. Three numbers 6, p and 12 are in Harmonic Progression if p =?
Q5. Find the value of the Harmonic Progression’s 22st and nth terms: 1/5, 1/9, 1/13, 1/14…..?
FAQs on Harmonic Progression
What is Harmonic Progression?
A Harmonic Progression (HP) is defined as a sequence of real numbers obtained by taking the reciprocals of an Arithmetic Progression that excludes 0. For example, if we have a sequence like a, b, c, d, … forming an Arithmetic Progression, the corresponding Harmonic Progression is represented as 1/a, 1/b, 1/c, 1/d, …
What is Harmonic Progression Formula?
If the Arithmetic Progression is written in the form: a, a+d, a+2d, a+3d,…a+(n−1)d
Then the Harmonic Progression formula is as follows: 1/a, 1/a+d, 1/a+2d, 1/a+3d,…
What is Sum of Harmonic Progression Formula?
To find the Sum of n terms in a Harmonic Progression (Sn) for the sequence 1/a, 1/a+d, 1/a+2d, …, 1/a+(n−1)d, the formula is Sn= 1/d.ln{2a+(2n−1)d} /(2a − d)}.
What is Harmonic Mean?
In a Harmonic Progression, each term of the series is the Harmonic Mean of its adjacent terms. The Harmonic Mean is computed as the reciprocal of the Arithmetic Mean of the reciprocals.
What is Harmonic Sequence?
A Sequence is classified as a Harmonic Sequence when the reciprocals of its elements or numbers create an Arithmetic Sequence. In a Harmonic Sequence, the progression takes the form of reciprocals: 1/a1, 1/a2, 1/a3, …, 1/an.
What Is an Example of Harmonic Progression?
An example of Harmonic Progression is 1/3, 1/6, 1/9, 1/12, 1/15……
How do we Solve Harmonic Progression?
The Harmonic Progression is solved by taking its reciprocal to form the Arithmetic Progression. Subsequently, determining the initial term and the common difference is necessary for further analysis. With these parameters, we can solve either the nth term or the sum of n terms within the Harmonic Progression.
Is the Sum of Harmonic Series infinite?
The Harmonic series is characterized by terms that tend to zero. However, the cumulative sum sequence for this series progressively increases infinitly. As a result, the series does not possess a finite sum. Instead, the sum of the initial n terms is referred to as the n-th partial sum of the series.
How much does limitless Harmonic Progession add up to?
The sum of infinite Harmonic Progression: by ∑∞a = 1a = 1 + 1/2 + 1/3 + 1/4 +… Infinite harmonic progressions cannot be added together. This series diverges rather than converges.
What is the Application or Use of Harmonic Progression?
Harmonic progression finds significant applications in various domains:
- Scientific Experimentation Precision: Scientists utilize harmonic formulae to determine experiment values accurately.
- Boiling Point Variation in Water: Harmonic progression aids in understanding how the boiling point of water changes with consistent alterations in temperature.
- Musical Notes: The concept of harmonic sequence is fundamental in music theory, particularly in understanding musical notes.
- Rainfall Estimation and Weather: Harmonic progression is employed to estimate rainfall, the concept’s applicability in weather forecasting and related domains.
What is the Relation between Arithmetic Mean, Geometric Mean and Harmonic Mean?
The relation between Arithmetic Mean, Geometric Mean and Harmonic Mean is given as GM2 = AM × HM
Share your thoughts in the comments
Please Login to comment...