Number of Tangents from a Point on a Circle
Last Updated :
07 May, 2021
A circle is a collection of all the points in a plane that are at a constant distance from a particular point. This distance is called the radius of the circle and the fixed point is called the centre. A straight line and a circle can co-exist in three ways, one can be a straight line with no intersection to the circumference of the circle, there always exists some space between the circle and the line. The second type is when the line lies in such a way that it passes touching the circumference of the circle, known as the Tangents of the circle. The third type is when the line intersects the circumference at two places and is known as a Secant. They are shown below,
- No Intersection
- Tangent
- Secant
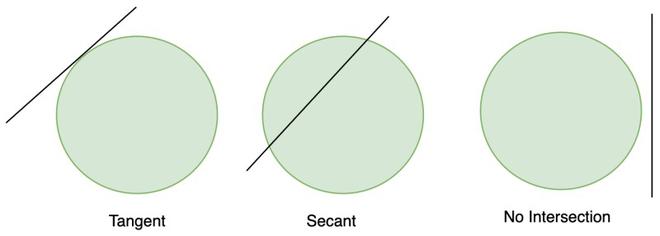
A secant intersects the circle at two points while a tangent intersects at only one point. Let’s study tangents and their properties in detail.
Tangents

A line intersecting circle at only one point is called a tangent. A circle has infinitely many possible tangents. The common point of tangent and the circle is called the point of contact.
Let’s see some properties of tangents through theorems.
Number of Tangents from a Point to a Circle
It is already known that a Tangent is defined as the line that passes touching the circle’s circumference. To get the idea for this, we need to perform some experiments, There are three cases that can be obtained through the different experiments.
Case 1: Tangent from inside a Circle
Let’s try to draw a tangent from inside a circle. Let’s assume a point P inside the circle and try to draw tangents. We observe that it is not possible to draw tangents from inside the circle.

Case 2: A point on the circle
We can see that in the figure at the beginning of the article that we can draw a tangent from any point on the circle. In fact, there can be an infinite number of tangents on a circle.
Case 3: A point outside the circle

We can see in the figure that from a point outside the circle, we can draw two tangents to it.
So, to summarize both the cases:
- There is no tangent to a circle from a point inside the circle.
- There is one tangent to a circle from a point that is on the circle.
- There are two tangents possible to a circle from a point that is outside the circle.
Properties of Tangents
Theorem 1:
The tangent at any point of a circle is perpendicular to the radius through the point of contact.
Proof:
Let’s assume a circle with centre O and a tangent XY to circle.

Let’s assume any point Q on the line XY and join the point of contact with centre. The diagram will look like this,

Now the point Q when joined to centre forms OQ, if it is extended it will become a secant not tangent. Now we can see that,
OQ > OP
This is true when Q is any point on the line XY except the point of contact (P). P is the point on line XY whose distance is shortest from the centre O. Thus, OP must be perpendicular to XY.
Hence, Proved.
This theorem allows us to conclude some other properties also:
- At any point in the circle, there can be only one tangent.
- The line joining the point of contact and centre is perpendicular to the tangent. Thus, it is also called normal to the tangent.
Theorem 2:
A line drawn through the end of the radius and perpendicular to it is a tangent to the circle.

Proof:
Let’s assume a circle with centre O in which OP is the radius. A line AB goes through P such OP is perpendicular to AB.
Now, take a point Q online AB. We know that the distance of Q is shortest from O when Q = P. In every other case,
OQ > OP and Q lies outside the circle. That means AB meets the circle at only one point P. Thus AB is tangent to the circle.
Question 1: In the diagram given below. Two tangents are drawn from an external point which is 41 cm from the centre. The radius of the circle is given as 9 cm. Find the area of the quadrilateral AOBC.

Solution:
We know from the previous theorem that line joining the centre from point of contact is perpendicular to the tangent. This makes OAC and OBC right-angled triangles.
So now,
Area of quadrilateral AOBC = Area of triangle AOC + Area of triangle BOC.
Area of triangle AOC = 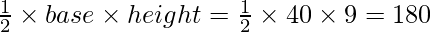 sq units.
sq units.
Since both the triangles are congruent, both have the same area. Thus, area of BOC = 180 sq units.
Area of quadrilateral AOBC = 180 + 180
= 360 sq units.
Question 2: Let’s assume a tangent AB at point A on the circle whose radius is 3cm. The distance of point B from the centre O is 5cm. Find out the length of AB.
Solution:
This is also an application of the theorem studied above, let’s make a diagram first.

We can see a right-angled triangle AOC here ,
OC2 = OA2 + AC2
52 = 32 + AC2
25 = 9 + AC2
16 = AC2
AC = 4cm
Theorem 3:
The lengths of tangents drawn from an external point to a circle are equal.
Proof:
Let’s assume a circle with centre O, a point C lying outside the circle and the tangents from that point to the circle. AC and BC are the tangents from the point. Our goal is to prove AC = BC.

Let’s join OA and OB and consider the two triangles OAC and OBC.
- OC is common.
- ∠OAC = ∠OBC (Right angled triangle)
- OA = OB (Radii of the circle)
Using RHS property we can say that these two triangles are congruent. Thus, AC = BC.
Theorem 4:
If two tangents are drawn from an external point then
- They subtend an equal angle at the centre, and
- They are equally inclined to the line segment joining the centre to that point.
Proof:

In the given figure, we need to prove that
∠POA = ∠POB and ∠OPA = ∠OPB.
Let us consider the two triangles, POA and POB.
PA = PB (By previous theorem)
OA = OB (radii of the circle)
OP = OP (Common)
Thus, these two triangles are congruent. [by SSS]
Hence, ∠POA = ∠POB and ∠OPA = ∠OPB.
Sample Problems
Question 1: In the given figure, AC and BC are the two tangents drawn from point C. Prove that 2∠OAB = ∠ACB.

Solution:
We know from the previous theorem that, AC = BC. This concludes that triangle ABC is an isosceles triangle.
We also know that ∠OAC = 90°. So,
∠BAC = 90° – ∠OAB
In triangle BAC
∠BAC + ∠ABC + ∠ACB = 180°
2∠BAC + ∠ACB = 180°
2(90° – ∠OAB) + ∠ACB = 180°
180° – 2∠OAB + ∠ACB = 180°
∠ACB = 2∠OAB
Question 2: There is a circle inscribed in a quadrilateral PQRS, prove that PQ + RS = PS + QR.

Solution:
A circle is inscribed inside the quadrilateral PQRS. Notice that the sides of the quadrilateral are actually tangents to the circle.
PA = PB,
BQ = QC
DR = RC
SA = SD
We need to prove PQ + RS = PS + QR.
Taking the L.H.S,
PQ + RS
⇒ PB + BQ + DR + DS
⇒ PA + CQ + RC + AS (From the relations stated above)
⇒ (PA + AS) + (CQ + RC)
⇒ PS + QR
Hence Proved
Question 3: In concentric circles, prove that chord of the larger circle which touches the smaller circle is bisected at the point of contact.
Answer:

Let’s say C1 and C2 are two concentric circles. Centre is O and AB is the chord of larger circle. From the previous theorems we know that, OP is perpendicular to AB. As we know from the properties of circle, that perpendicular from the centre bisects the chord.
AB is chord to larger circle C1 and OP is perpendicular to it. Thus is bisects the chord.
Share your thoughts in the comments
Please Login to comment...