Unit Circle is a Circle whose radius is 1. The center of unit circle is at origin(0,0) on the axis. The circumference of Unit Circle is 2π units, whereas area of Unit Circle is π units2. It carries all the properties of Circle. Unit Circle has the equation x2 + y2 = 1. This Unit Circle helps in defining various Trigonometric concepts.

Unit Circle
The Unit Circle is often denoted as S1 generalization to higher dimensions is the unit sphere. Let’s understand more about Unit Circle, Formula and Solved examples in detail below.
What is Unit Circle?
Unit Circle is a circle that has a radius of One(1) unit. We use the cartesian plane to draw a unit circle and a unit circle is a 2-degree polynomial with two variables. The unit circle has various applications in trigonometry and algebra and is majorly used to find the values of different trigonometric ratios such as sin x, cos x, tan x, and others.
Unit Circle Definition
In Mathematics, we define a unit circle as the locus of a fixed point that is at a distance of one unit from the center of the circle. A unit circle has a radius of one unit and hence the name unit circle.
Equation of Unit Circle
We know that the equation of any circle with center (h, k) and radius ‘r’ is,
(x – h)2 + (y – k)2 = r2
For a unit circle we know that r is 1 unit and so the equation of the unit circle is,
(x – h)2 + (y – k)2 = 1
Formula of Unit Circle
If the center of the unit circle is origin, i.e. (h, k) = (0, 0) then the equation of unit circle is,
x2 + y2 = 1
A unit circle is represented in the image added below, with center coordinate h, k and when the circle is at origin the value of h and k is zero and the radius AP is equal to 1 unit.

Trigonometric Functions Using Unit Circle
The application of the Pythagoras theorem in a unit circle can be better used to understand trigonometric functions. For this, we consider a right triangle to be placed inside a unit circle in the Cartesian coordinate plane. If we notice, the radius of this circle denotes the hypotenuse of the right-angled triangle.
The radius of the circle forms a vector. This leads to the formation of an angle, say θ with the positive x-axis. Let us suppose x to be the base length and y to be the altitude length of the right triangle respectively. Also, the coordinates of the radius vector endpoints are (x, y) respectively.
The right-angle triangle holds the sides 1, x, and y respectively. The trigonometric ratio can be computed now, as follows:
sin θ = Altitude/Hypotenuse = y/1
cos θ = Base/Hypotenuse = x/1
Now,
- sin θ = y
- cos θ = x
- tan θ = sin θ /cos θ = y/x
On substituting the values of θ, we can obtain principal values of all the trigonometric functions. Simillarly values of trigonometric functions at different values is found.
Unit Circle with Sin Cos and Tan
Any point on the unit circle with the coordinates (x, y), is represented using trigonometric identies as, (cosθ, sinθ). The coordinates of the radius corners represent the cosine and the sine of the θ values for a particular value of θ and the radius line. We have cos θ = x, and sin θ = y. There are four parts of a circle each lying in one quadrant, making an angle of 90°,180°, 270°, and 360°. The radius values lie between -1 to 1 respectively. Also, the sin θ and cos θ values lie between 1 and -1 respectively.
Unit Circle and Trigonometric Identities
The unit circle trigonometric identities for cotangent, secant, and cosecant can be computed using the identities for sin, cos, and tan. Conclusively, we obtain a right-angled triangle with the sides 1, x, and y respectively. Computing the unit circle identities can be expressed as,
- sin θ = y/1
- cos θ = x/1
- tan θ = y/x
- sec θ = 1/x
- cosec θ = 1/y
- cot θ = x/y
Unit Circle Chart
The unit circle chart is a chart that contains the value of the trigonometric function sine and cosine for various angles. The unit circle chart for the same is added below,
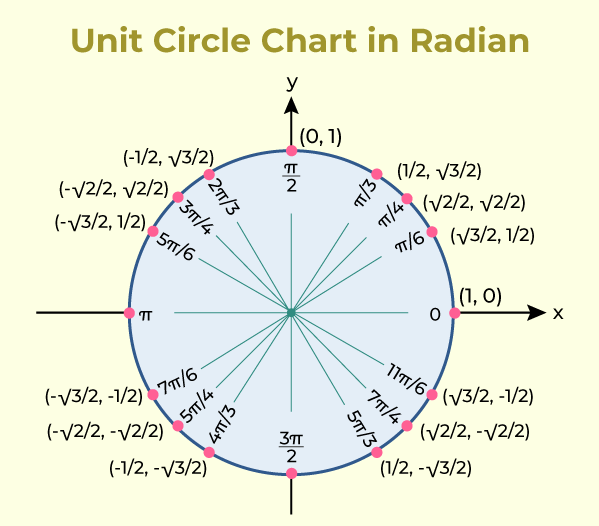
Unit Circle Table
The trigonometric ratios used in the unit circle table are used to list the coordinates of the points on the unit circle that correspond to common angles.
|
Angles
|
0°
|
30°
|
45°
|
60°
|
90°
|
|
sin
|
0
|
1/2
|
1/√(2)
|
√3/2
|
1
|
|
cos
|
1
|
√3/2
|
1/√(2)
|
1/2
|
0
|
|
tan
|
0
|
1/√(3)
|
1
|
√(3)
|
Not Defined
|
|
csc
|
Not Defined
|
2
|
√(2)
|
2/√(3)
|
1
|
|
sec
|
1
|
2/√(3)
|
√(2)
|
2
|
Not Defined
|
|
cot
|
Not Defined
|
√(3)
|
1
|
1/√(3)
|
0
|
Unit Circle Pythagorean Identities
There are three Pythagorean Identities and all of them are easily proved using the concept of the unit circle the three Pythagorean identities are,
- sin2θ + cos2θ = 1
- 1 + tan2θ = sec2θ
- 1 + cot2θ = cosec2θ
Unit Circle Complex Plane
Complex Numbers and Complex Plane are easily explained using the concept of unit circle. The equation of unit circle in complex form is,
|z| = 1
OR
x2+ y2 = 1
In Euler’s Form complex number is represented as,
z = eit = cos t + i(sin t)
Read More
Solved Examples on Unit Circle
Q1: Prove that point Q lies on a unit circle, Q = [1/√(6), √4/√6]
Solution:
Given,
x = 1/√(6), y = √4/√6
Equation of Unit Circle is,
x2 + y2 = 1
LHS = (1/√(6))2 + (√4/√6)2
LHS = 1/6 + 4/6 = 5/6 ≠ 1
LHS ≠ RHS
Thus, point Q[1/√(6), √4/√6] does not lie on the unit circle.
Q2: Compute tan 30o using the sin and cos values of the unit circle.
Solution:
tan 30° using sin and cos values,
tan 30° = (sin 30°)/ (cos 30°)
- sin 30° = 1/2
- cos 30° = √(3)/2
tan 30° = 1/2/√(3)/2
tan 30° = 1/√(3)
Q3: Validate if the point P [1/2, √(3)/2] lies on the unit circle.
Solution:
Given,
P = [1/2, √(3)/2]
Equation of Unit Circle is,
LHS
= (1/2)2 + (√(3)/2)2
= 1/4 + 3/4
= (1 + 3)/4 = 4/4
= 1
= RHS
Practice Questions on Unit Circle
Q1. Check If the points A (1/2, 3/2) lies on a unit circle.
Q2. Check If the points A (2, 1/2) lies on a unit circle.
Q3. Find the value of cos 240°
Q4. Find the value of tan 320°
Q5. Find the value of sin 160°
Unit Circle – FAQs
What is Unit Circle?
A unit circle is defined as the location of a point one unit away from a fixed point. It has a center at (0,0) and value of its radius is 1.
How to check If a Point Lies on Unit Circlet?
Any point lying in a 2D plane that is of the form (x, y) is put in the unit circle equation x2 + y2 = 1 to verify if it lies on the circle or not.
What is the formula of Unit Circle?
The unit circle formula is a formula that is used to represent a unit circle algebraically. The unit circle formula is given as,
x2 + y2 = 1
Why is it Called Unit Circle?
A unit circle is called unit circle because it has a radius of one(1) units.
Share your thoughts in the comments
Please Login to comment...