Constructions of Tangents to a Circle
Last Updated :
05 May, 2021
A line can pass through a circle in three ways- it can either pass through only a single point of the circle, intersect it, or it can pass outside it. A line passing through a single point of a circle is called a tangent. When a line intersects the circle at two points, we call that line a tangent. Architects and designers use this concept every day in their work. In such cases, it becomes essential to know how to construct a tangent to a circle from a point that is outside the circle. Let’s look at that procedure in detail.
Tangent
The tangent of a circle is a line that intersects the circle at a single point. The figure given below shows an example of a tangent passing through a circle. The point at which the tangent intersects the circle is called the point of contact. Notice that the tangent is also perpendicular to the line joining the point of contact with the circle.

Note: The lines which intersect circles at two points are called secants.

Construction of Tangent
Two tangents can be drawn from any point outside the circle. Our goal is to learn how to construct a single tangent from any point that is given outside the circle. The other tangent can be drawn in a similar manner.
Steps of Construction:
We are given a circle with centre O with a radius “r” and a point A outside the circle. Let’s see how to construct a tangent from point A to the circle.
Step 1. Draw a circle with radius r and let’s call its centre O. Draw a point A outside the circle.

Step 2. Join OA and bisect it. We’ll call its midpoint M.

Step 3. Now with M as centre and radius MA. Draw a circle that intersects the given circle at points B and C.

Step 4. Join AB and AC. They are our given tangents.

Sample Problems
Question 1: Draw a tangent from a point P which is 10cm from the centre O of the circle of radius 5cm.
Solution:
Circle with centre O with a radius “5cm” and a point P outside the circle.
Step 1. Draw a circle with radius 5cm and let’s call its centre O. Draw a point A which is 10cm from the centre outside the circle.

Step 2. Join OP and bisect it. We’ll call its midpoint M.

Step 3. Now with M as centre and radius MP. Draw a circle that intersects the given circle at points Q and R.

Step 4. Join PQ and PR. They are our given tangents.

Question 2: Draw a tangent from a point P which 6cm from the centre O of the circle of radius 3cm.
Solution:
Circle with centre O with a radius “3cm” and a point P outside the circle.
Step 1. Draw a circle with radius 3cm and let’s call its centre O. Draw a point A which is 6cm from the centre outside the circle.

Step 2. Join OP and bisect it. We’ll call its midpoint M.

Step 3. Now with M as centre and radius MP. Draw a circle that intersects the given circle at points Q and R.

Step 4. Join PQ and PR. They are our given tangents.

Question 3: How many parallel tangents are possible in a circle?
Answer:
There are at max two possible parallel tangents in a circle. They lie on diametrically opposite points.

Question 4: Draw a tangent from a point P which 15cm from the centre O of the circle of radius 5cm.
Solution:
Circle with centre O with a radius “15cm” and a point P outside the circle.
Step 1. Draw a circle with radius 5cm and let’s call its centre O. Draw a point A which is 15cm from the centre outside the circle.

Step 2. Join OP and bisect it. We’ll call its midpoint M.

Step 3. Now with M as centre and radius MP. Draw a circle that intersects the given circle at points Q and R.

Step 4. Join PQ and PR. They are our given tangents.

Question 5: Draw tangents from a point P inclined at 30° from the line joining the point and the centre of the circle of radius 8cm.
Solution:
Circle with centre O with a radius “8cm” and a point P outside the circle.
We know that the tangents are inclined at 30°. Let’s say they intersect the circle at R and Q. It makes a triangle OPR. We need to know the length of OP. We also know that OR is perpendicular to PR. Thus, it’s a right-angled triangle, and we can use trigonometric formulas to find out OP.
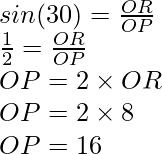
Thus, OP is 16cm. Now we can construct a tangent.
Step 1. Draw a circle with radius 8cm and let’s call its centre O. Draw a point P which is 16cm from the centre outside the circle.

Step 2. Join OP and bisect it. We’ll call its midpoint M.

Step 3. Now with M as centre and radius MP. Draw a circle that intersects the given circle at points Q and R.
Step 4. Join PQ and PR. They are our given tangents.

Question 6: Draw a tangent from a point P which 11cm from the centre O of the circle of radius 6cm.
Solution:
Circle with centre O with a radius “6cm” and a point P outside the circle.
Step 1. Draw a circle with radius 6cm and let’s call its centre O. Draw a point A which is 11cm from the centre outside the circle.

Step 2. Join OP and bisect it. We’ll call its midpoint M.

Step 3. Now with M as centre and radius MP. Draw a circle that intersects the given circle at points Q and R.

Step 4. Join PQ and PR. They are our given tangents.

Share your thoughts in the comments
Please Login to comment...