Volume of a Cylinder is the amount of space contained within the three-dimensional boundaries of the cylinder. Volume of a Cylinder formula is πr2h where r denotes the radius of the base and h is the height of the cylinder.
A cylinder is a 3-dimensional solid figure with two identical bases connected by a curving surface. It can be considered as a collection of many congruent disks, stacked one above the other. The height of a cylinder is simply the length from its top to the bottom base, and the radius of any of its bases is the cylinder’s base itself.
In this article, we will learn about, Volume of a Cylinder Definition, Volume of a Cylinder Formula, and How to Calculate Volume of a Cylinder.
What is a Cylinder?
Cylinder in mathematics is defined as any that has two circular bases and a curved surface that connects them. For example, Gas cylinders and Rolling Pin in our houses resemble cylindrical shapes.
Cylinder Definition
Cylinder is defined as a 3-D figure in which the base are circle and both surfaces are connected by a curved surface.
Types of Cylinders
Below are 5 different types of cylinders:
Right Circular Cylinder: A three-dimensional geometric figure with two circular bases aligned directly above each other, and the axis (line connecting the centers of the circular bases) is perpendicular to the center of the bases.
Oblique Cylinder: A cylinder where the axis is not perpendicular to the center of the circular bases. In other words, the circular bases are not directly above each other.
Elliptic Cylinder: A cylinder with elliptical (oval-shaped) bases instead of circular bases. The axis remains straight, passing through the center of both elliptical bases.
Right Circular Hollow Cylinder: A cylindrical shape with two concentric circular bases (one inside the other), creating a hollow space between them. The axis is perpendicular to the centres of both circular bases.
Right Circular Solid Cylinder: A cylindrical shape characterised by having two congruent circular bases aligned directly above each other. The axis, which is a straight line connecting the centres of the circular bases, is perpendicular to the center of these bases. Unlike a hollow cylinder, a solid cylinder has no empty space within it; it is a continuous, filled structure.
What is Volume of Cylinder?
Volume of a cylinder is the total capacity of any cylinder, i.e. the total amount of liquid any cylinder can hold. It is generally measured in liters, volume can also be measured in m3, cm3, etc. Volume of Cylinder is calculated by multiplying area of circular base (πr2) of cylinder by its height (h).
Volume of Cylinder Definition
Volume of cylinder is a measure of space enclosed within its 3-D shape. For any cylinder of height ‘h’ and radius ‘r’ volume of cylinder is πr2h.
Volume of Solid Cylinder
Volume of a cylinder is also equal to the amount of space taken by it in a three-dimensional space. In other words, it determines the space or region enclosed by the cylinder is its volume, and the unit of volume is cubic unit i.e., the number of unit cubes (cubes of unit length) that may fit into an object.
Volume of Cylinder Formula V = πr2h is also called Volume of Cylinder Equation.

Volume of Cylinder
Volume of a Right Circular Cylinder
In the Right Circular Cylinder angle between the plane of the base or top and the curved surface is a right angle. For a right circular cylinder, the base is a circle with radius r, thus its area is πr2, and the height of the cylinder is h then the volume of the cylinder is:
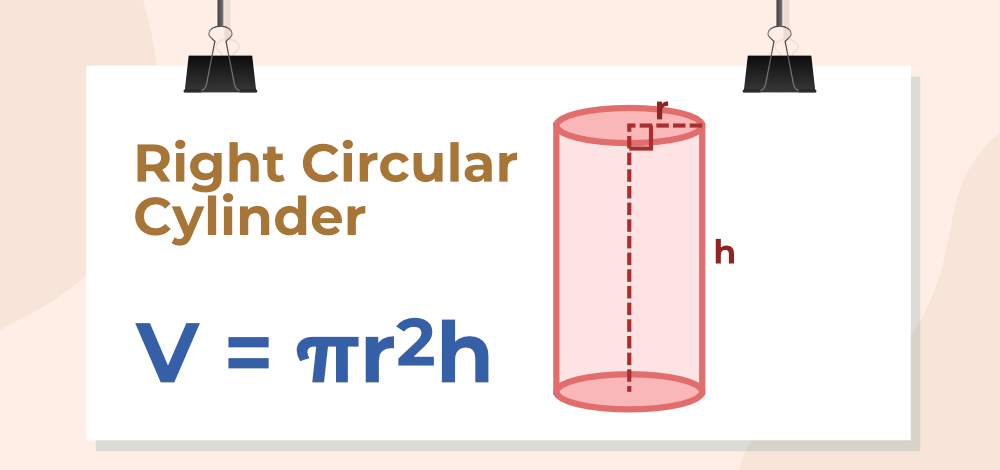
Volume of Right Circular Cylinder
Volume of a Hollow Cylinder
A hollow cylinder is a cylinder that is hollow from the inside thus, its bases form a ring with two radii inner radius and an outer radius. Suppose a hollow cylinder is taken with its inner radius as r and outer radius as R and the height of the cylinder is h then volume of hollow cylinder is given as:

Volume of a Hollow Cylinder
Volume of an Oblique Cylinder
In an Oblique Cylinder angle between the plane of the base or top and the curved surface is not a right angle, but volume is given by the same formula as a product of the area of the base and the height of the cylinder.

Volume of Oblique Cyllinder
Volume of an Elliptic Cylinder
A cylinder; with an ellipse as its base instead of a circle, is known as Elliptic Cylinder. Let both radii of the base which is an ellipse be a and b and the height of the cylinder be h, then

Volume of Elliptic Cylinder
How To Calculate Volume of a Cylinder?
Let’s take an example to understand how we can calculate the volume of a cylinder.
Example: Calculate the volume of a cylinder of radius 4 m and height 5 m.
Step 1: Note the radius and height of cylinder. In this example, the radius of the cylinder is 4 m and height is 5 m.
Step 2: We know that the volume of a cylinder is equal to πr2h. Substitute the given value of radius and height in the formula.
Step 3: So, the volume of cylinder is calculated as, 3.14 × (4)2 × 5 = 251.20 cu. m.
Volume of Cylinder in Liters
Generally, the volume of a cylinder is calculated in cubic meters or cubic centimetres but we can change them in litres by using the conversion discussed below i.e.,
1 cm3 = 1 ml
1000 cm3 = 1 litre
1 m3 = 1000000 cm3 = 1000 litres
Example: If a cylinder has a volume of 32 m3 it can be written as 32×1000 litres = 32000 litres
Some formulas for cylinder other than volume formulas are,
Surface Area of a Cylinder
Surface Area of any figure is defined as the area required to totally cover the surface of any object. So, the surface area of a cylinder can be defined as the area required to cover the surface of the cylinder.
CSA of a Cylinder
Curved Surface Area or CSA is the area of the surface that is not flat but rounded. So, the CSA of the cylinder is all the surface except the base and top. If r is the radius of the base and h is the height of the cylinder, then CSA is given as follows:
CSA of Cylinder = 2πrh
TSA of a Cylinder
Total Surface Area or TSA is the area of the completer surface of the cylinder. So, TSA is the sum of the CSA and the area of the top as well as the base of the cylinder. So, if the base radius of the cylinder is r and the height of the cylinder is h then TSA is given by,
TSA of cylinder = 2πr(r+h)
Related Reads,
Volume of Cylinder Examples
Example 1: Calculate the volume of a cylinder of radius 3 m and a height of 4 m. (take π = 3.14)
Solution:
We have, r = 3 and h = 4
Using the formula we have,
V = πr2h
⇒ V = 3.14 × (3)2 × 4
⇒ V = 113.04 m3
Example 2: Calculate the volume of a cylinder of radius 4 m and a height of 7 m.
Solution:
We have, r = 4 and h = 7
Using the formula we have,
V = πr2h
⇒ V = 3.14 × (4)2 × 7
⇒ V = 351.68 m3
Example 3: Calculate the radius of a cylinder if its volume is 300 m3 and height is 7 m.
Solution:
We have, V = 300 and h = 7
Using the formula we have,
V = πr2h
⇒ r2 = V/πh
⇒ r2 = 300/(3.14 × 7)
⇒ r = 3.68 m
Example 4: Calculate the radius of a cylinder if its volume is 450 m3 and its height is 9 m.
Solution:
We have, V = 450 and h = 9
Using the formula we have,
V = πr2h
⇒ r2 = V/πh
⇒ r2 = 450/(3.14 × 9)
⇒ r = 12.52 m
Example 5: Calculate the height of a cylinder if its volume is 570 m3 and its radius is 4 m.
Solution:
We have, V = 570 and r = 4
Using the formula we have,
V = πr2h
⇒ h = V/πr2
⇒ h = 570/(3.14 × 4 × 4)
⇒ h = 11.34 m
Example 6: Calculate the height of a cylinder if its volume is 341 m3 and its radius is 6 m.
Solution:
We have,
V = 341 m3
r = 6 m
Using the formula we have,
V = πr2h
⇒ h = V/πr2
⇒ h = 341/(3.14 × 6 × 6)
⇒ h = 3.01 m
Practice Questions on Volume of Cylinder
Q1: Find Volume of Cylinder whose diameter is 14 cm and height is 12 cm.
Q2: Find Volume of Cylinder whose surface area of base is 84 cm2 and height is 11 cm.
Q3: Find the height of cylinder whose radius is 7 cm and volume is 770 cm3
Q4: Find the volume of a hollow cylinder of height 13 cm whose inner radius is 6 cm and outer radius is 1 cm.
Volume of Cylinder-FAQs
What is Volume of a Cylinder?
Volume of a cylinder is defined as the capacity of the cylinder, i.e. the amount of substance a cylinder can hold. It can also be defined as the total material required for making a cylinder.
What is Formula for the Volume of a Cylinder?
Volume of the cylinder (V) is given by the formula, V = (Area of Circular Base) × (Height) Or V = πr2h
What is Volume of a Cylinder if its Radius is Doubled?
As the volume of the circle is proportional to the square of the radius. So if the radius of the circle is doubled then its volume becomes four times.
What is Volume of Cylinder if its Radius is halved?
As the volume of the circle is proportional to the square of the radius. So if the radius of the circle is halved then its volume becomes one by four times.
What is Unit for Volume of a Cylinder?
Volume of a cylinder is measured in cubic units, i.e. cubic centimetres (cm3), cubic meters (m3), cubic feet (ft3) and so on for mathematical purposes. In general usage, it is also measured in Litters (l), millilitres (ml), etc.
What Volume of Cylinder with Diameter and Height?
If the diameter of a cylinder is d then its radius is given by radius = (diameter)/2 so r = d/2 and if its height is ‘h’, the volume of cylinder is measured by the formula, V = πdh/4 unit 3
What is Volume of a Hollow Cylinder?
If R is the external radius and r is the internal radius, then the formula for calculating the cylinder’s volume is given by: V = π (R2 – r2) h cubic units.
What is Volume of an Oblique Cylinder?
Formula to find the volume of an oblique cylinder is same as the volume of the cylinder and the volume of the oblique cylinder is calculated using the formula. V = π r2 h cubic units.
What is Volume of an Elliptical Cylinder?
Formula to find the volume of an Elliptical Cylinder is, V = πabh cubic units. Where, a and b are the radii of bases of the cylinder and h is the height of the cylinder.
What is Volume of a Solid Cylinder?
Volume of Solid Cylinder is the volume of material used in making the cylinder. For any solid cylinder of height ‘h’ and radius ‘r’ its volume is given by the formula, V = πr2h
What is Volume of Cylinder Calculator?
Volume of cylinder calculator is a tool which is used to find volume of the cylinder by inputting the value of radius and height of the cylinder as added above.
Share your thoughts in the comments
Please Login to comment...