Inscribed Shapes in a Circle – Problem Solving
Last Updated :
06 May, 2021
In Geometry, there is a specific classification where shapes are found within other shapes, for instance, a circle within a triangle, quadrilateral within a circle, etc. The shapes are called Inscribed and circumscribed. The inner shape is known as the “Inscribed shapes” while the outer shape is known as the “Circumscribed shapes”. Suppose a circle is Inscribed in any other shape (a polygon), the edges of the polygon (all touching the circle) are the tangents to the circle.

Right Angled Triangles Inscribed in a Circle
When a triangle is inserted in a circle in such a way that one of the sides of the triangle is the diameter of the circle then the triangle is a right triangle.

This is also referred to as Thales Theorem.
Proof:
The below diagram has the OC line segment added to it.

Since segments OB, OC, and OA are all radii of the same circle, they are all congruent. Therefore, both triangles COB and COA are isosceles triangles. Angles B and BCO are congruent since they are opposite congruent sides of the isosceles triangle COB. Similarly, angles A and ACO are congruent because they are opposite congruent sides of the triangle COA.
The sum of the measures of the three angles in a triangle is 180 degrees and so,
m(∠A) + m(∠B) + m(∠C) = 180
Using the angle equivalences from the previous paragraph
m(∠C) = m(∠BCO) + m(∠ACO)
= m(∠CBO) + m(∠CAO)
= m(∠B) + m(∠A)
Substituting this into the previous formula we find
2m(∠A) + 2m(∠B) = 180
and so m(∠A) + m(∠B) = 90. Since the measures of the three angles of triangle ABC add to 180 this means that m(∠C) = 90° and so triangle ABC is a right triangle as desired.
Question: Triangle ΔABC is inscribed in a circle O, and side AC passes through the circle’s centre. Find the circle’s diameter.

Answer:
We know that the triangle inscribed by a chord that passes through the centre of the circle is a right triangle.
Given, BC = 16 and AB = 12.
Hypotenuse theorem can be applied here,
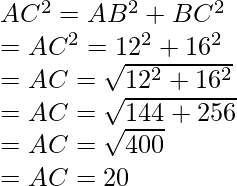
The diameter of the circle is 20.
Inscribed Angles in Circles
An Inscribed angle in a circle is defined in such a way that its two sides/rays are acting as the chord to the circle and the vertex of the angle is placed on the circumference of the circle.

When another angle is added whose vertex is placed at the centre and the rays meet the ends of the previous angle, the angle subtended by the centre angle becomes twice the angle subtended by the other angle.
Cyclic Quadrilaterals
When a quadrilateral is inscribed in a Circle such a way that all the vertices of the quadrilateral are touching the circumference of the circle. There are certain properties for the cyclic Quadrilateral.

Property: The Opposite angles of a cyclic quadrilateral always add up to give 180°. OR It can be said that the Opposite angles are Supplementary in Nature.
Here, ∠A + ∠C = 180°
∠B + ∠D = 180°
When all the angles are added, ∠A + ∠B + ∠C + ∠D = 180 + 180 = 360°
Question 1: In the figure below, find the other angle.

Answer:
Since both the angles inscribed are from the same arc, the angles must be equal.
So, the other angle is also 75o
Question 2: In the figure below, find the length of minor arc AC.

Answer:
By the theorem studied earlier, we know that the angle inscribed on the circle by an arc is half of the angle inscribed at the centre by that same arc. Therefore, ∠AOC = 60°.
Now we have the angle inscribed at the centre and the radius of the circle is 4cm(given).
The length of the arc can be found out by
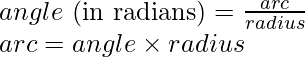
30° is given as 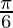 in radian.
in radian.
So, plugging the values in the above formula.

So, the length of the arc is 2.0943.
Question 3: In the given figure, CD is chord which is equal to the radius of the circle, AB is the diameter as shown, Chords AC and BD are extended outside the circle to meet at E. Prove that ∠AEB = 60°

Answer:
To Prove: ∠AEB = 60°
Construction: Join OC, OD and BC with dotted lines.
Proof: △COD is an equilateral triangle since all three sides are equal to the radius of the circle.
So, ∠COD= 60° and ∠CBD = 30° (half of the angle subtended at the centre)
In △ACB, ∠ACB = 90°
∠BCE= 180-90 (as AE is a straight line) = 90°
In △BCE, ∠BEC + 90+ 30 = 180°
∠BEC = 60°
Therefore, ∠AEB = 60°
Share your thoughts in the comments
Please Login to comment...