Introduction and implementation of Karger’s algorithm for Minimum Cut
Last Updated :
19 Apr, 2024
Given an undirected and unweighted graph, find the smallest cut (smallest number of edges that disconnects the graph into two components).
The input graph may have parallel edges.
For example consider the following example, the smallest cut has 2 edges.
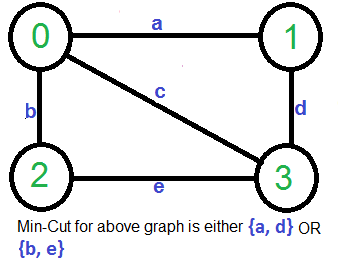
A Simple Solution use Max-Flow based s-t cut algorithm to find minimum cut. Consider every pair of vertices as source ‘s’ and sink ‘t’, and call minimum s-t cut algorithm to find the s-t cut. Return minimum of all s-t cuts. Best possible time complexity of this algorithm is O(V5) for a graph. [How? there are total possible V2 pairs and s-t cut algorithm for one pair takes O(V*E) time and E = O(V2)].
Below is simple Karger’s Algorithm for this purpose. Below Karger’s algorithm can be implemented in O(E) = O(V2) time.
1) Initialize contracted graph CG as copy of original graph
2) While there are more than 2 vertices.
a) Pick a random edge (u, v) in the contracted graph.
b) Merge (or contract) u and v into a single vertex (update
the contracted graph).
c) Remove self-loops
3) Return cut represented by two vertices.
Let us understand above algorithm through the example given.
Let the first randomly picked vertex be ‘a‘ which connects vertices 0 and 1. We remove this edge and contract the graph (combine vertices 0 and 1). We get the following graph.
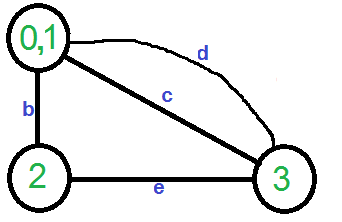
Let the next randomly picked edge be ‘d’. We remove this edge and combine vertices (0,1) and 3.
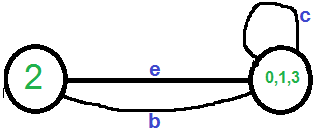
We need to remove self-loops in the graph. So we remove edge ‘c’
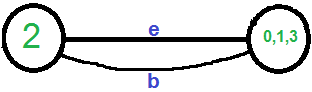
Now graph has two vertices, so we stop. The number of edges in the resultant graph is the cut produced by Karger’s algorithm.
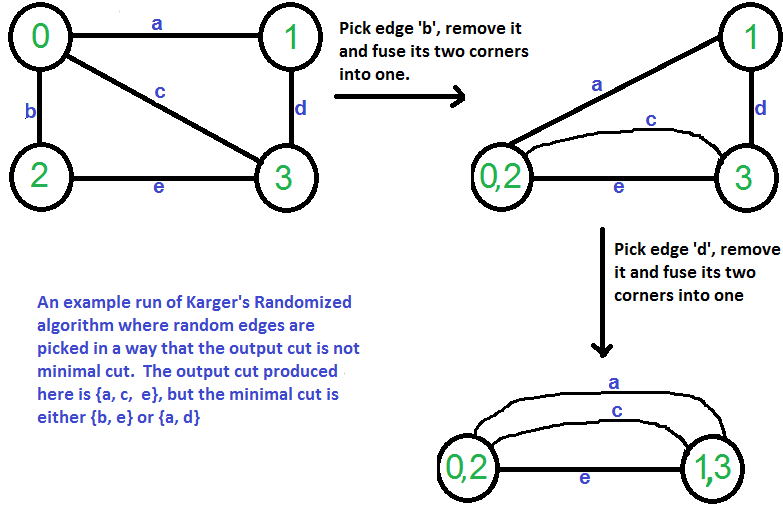
Karger’s algorithm is a Monte Carlo algorithm and cut produced by it may not be minimum. For example, the following diagram shows that a different order of picking random edges produces a min-cut of size 3.
Below is the implementation of above algorithm. The input graph is represented as a collection of edges and union-find data structure is used to keep track of components.
C++
// Karger's algorithm to find Minimum Cut in an
// undirected, unweighted and connected graph.
#include <iostream>
//#include <stdlib.h>
#include <time.h>
// a structure to represent a unweighted edge in graph
struct Edge
{
int src, dest;
};
// a structure to represent a connected, undirected
// and unweighted graph as a collection of edges.
struct Graph
{
// V-> Number of vertices, E-> Number of edges
int V, E;
// graph is represented as an array of edges.
// Since the graph is undirected, the edge
// from src to dest is also edge from dest
// to src. Both are counted as 1 edge here.
Edge* edge;
};
// A structure to represent a subset for union-find
struct subset
{
int parent;
int rank;
};
// Function prototypes for union-find (These functions are defined
// after kargerMinCut() )
int find(struct subset subsets[], int i);
void Union(struct subset subsets[], int x, int y);
// A very basic implementation of Karger's randomized
// algorithm for finding the minimum cut. Please note
// that Karger's algorithm is a Monte Carlo Randomized algo
// and the cut returned by the algorithm may not be
// minimum always
int kargerMinCut(struct Graph* graph)
{
// Get data of given graph
int V = graph->V, E = graph->E;
Edge *edge = graph->edge;
// Allocate memory for creating V subsets.
struct subset *subsets = new subset[V];
// Create V subsets with single elements
for (int v = 0; v < V; ++v)
{
subsets[v].parent = v;
subsets[v].rank = 0;
}
// Initially there are V vertices in
// contracted graph
int vertices = V;
// Keep contracting vertices until there are
// 2 vertices.
while (vertices > 2)
{
// Pick a random edge
int i = rand() % E;
// Find vertices (or sets) of two corners
// of current edge
int subset1 = find(subsets, edge[i].src);
int subset2 = find(subsets, edge[i].dest);
// If two corners belong to same subset,
// then no point considering this edge
if (subset1 == subset2)
continue;
// Else contract the edge (or combine the
// corners of edge into one vertex)
else
{
printf("Contracting edge %d-%d\n",
edge[i].src, edge[i].dest);
vertices--;
Union(subsets, subset1, subset2);
}
}
// Now we have two vertices (or subsets) left in
// the contracted graph, so count the edges between
// two components and return the count.
int cutedges = 0;
for (int i=0; i<E; i++)
{
int subset1 = find(subsets, edge[i].src);
int subset2 = find(subsets, edge[i].dest);
if (subset1 != subset2)
cutedges++;
}
return cutedges;
}
// A utility function to find set of an element i
// (uses path compression technique)
int find(struct subset subsets[], int i)
{
// find root and make root as parent of i
// (path compression)
if (subsets[i].parent != i)
subsets[i].parent =
find(subsets, subsets[i].parent);
return subsets[i].parent;
}
// A function that does union of two sets of x and y
// (uses union by rank)
void Union(struct subset subsets[], int x, int y)
{
int xroot = find(subsets, x);
int yroot = find(subsets, y);
// Attach smaller rank tree under root of high
// rank tree (Union by Rank)
if (subsets[xroot].rank < subsets[yroot].rank)
subsets[xroot].parent = yroot;
else if (subsets[xroot].rank > subsets[yroot].rank)
subsets[yroot].parent = xroot;
// If ranks are same, then make one as root and
// increment its rank by one
else
{
subsets[yroot].parent = xroot;
subsets[xroot].rank++;
}
}
// Creates a graph with V vertices and E edges
struct Graph* createGraph(int V, int E)
{
Graph* graph = new Graph;
graph->V = V;
graph->E = E;
graph->edge = new Edge[E];
return graph;
}
// Driver program to test above functions
int main()
{
/* Let us create following unweighted graph
0------1
| \ |
| \ |
| \|
2------3 */
int V = 4; // Number of vertices in graph
int E = 5; // Number of edges in graph
struct Graph* graph = createGraph(V, E);
// add edge 0-1
graph->edge[0].src = 0;
graph->edge[0].dest = 1;
// add edge 0-2
graph->edge[1].src = 0;
graph->edge[1].dest = 2;
// add edge 0-3
graph->edge[2].src = 0;
graph->edge[2].dest = 3;
// add edge 1-3
graph->edge[3].src = 1;
graph->edge[3].dest = 3;
// add edge 2-3
graph->edge[4].src = 2;
graph->edge[4].dest = 3;
// Use a different seed value for every run.
srand(time(NULL));
printf("\nCut found by Karger's randomized algo is %d\n",
kargerMinCut(graph));
return 0;
}
// Java program to implement the Karger's algorithm to find
// Minimum Cut in an
// undirected, unweighted and connected graph.
import java.io.*;
import java.util.*;
class GFG {
// a structure to represent a unweighted edge in graph
public static class Edge {
int src, dest;
Edge(int s, int d)
{
this.src = s;
this.dest = d;
}
}
// a structure to represent a connected, undirected
// and unweighted graph as a collection of edges.
public static class Graph {
// V-> Number of vertices, E-> Number of edges
int V, E;
// graph is represented as an array of edges.
// Since the graph is undirected, the edge
// from src to dest is also edge from dest
// to src. Both are counted as 1 edge here.
Edge edge[];
Graph(int v, int e)
{
this.V = v;
this.E = e;
this.edge = new Edge[e];
/*for(int i=0;i<e;i++){
this.edge[i]=new Edge(-1,-1);
}*/
}
}
// A structure to represent a subset for union-find
public static class subset {
int parent;
int rank;
subset(int p, int r)
{
this.parent = p;
this.rank = r;
}
}
// A very basic implementation of Karger's randomized
// algorithm for finding the minimum cut. Please note
// that Karger's algorithm is a Monte Carlo Randomized
// algo and the cut returned by the algorithm may not be
// minimum always
public static int kargerMinCut(Graph graph)
{
// Get data of given graph
int V = graph.V, E = graph.E;
Edge edge[] = graph.edge;
// Allocate memory for creating V subsets.
subset subsets[] = new subset[V];
// Create V subsets with single elements
for (int v = 0; v < V; ++v) {
subsets[v] = new subset(v, 0);
}
// Initially there are V vertices in
// contracted graph
int vertices = V;
// Keep contracting vertices until there are
// 2 vertices.
while (vertices > 2) {
// Pick a random edge
int i = ((int)(Math.random() * 10)) % E;
// Find vertices (or sets) of two corners
// of current edge
int subset1 = find(subsets, edge[i].src);
int subset2 = find(subsets, edge[i].dest);
// If two corners belong to same subset,
// then no point considering this edge
if (subset1 == subset2) {
continue;
}
// Else contract the edge (or combine the
// corners of edge into one vertex)
else {
System.out.println("Contracting edge "
+ edge[i].src + "-"
+ edge[i].dest);
vertices--;
Union(subsets, subset1, subset2);
}
}
// Now we have two vertices (or subsets) left in
// the contracted graph, so count the edges between
// two components and return the count.
int cutedges = 0;
for (int i = 0; i < E; i++) {
int subset1 = find(subsets, edge[i].src);
int subset2 = find(subsets, edge[i].dest);
if (subset1 != subset2) {
cutedges++;
}
}
return cutedges;
}
// A utility function to find set of an element i
// (uses path compression technique)
public static int find(subset subsets[], int i)
{
// find root and make root as parent of i
// (path compression)
if (subsets[i].parent != i) {
subsets[i].parent
= find(subsets, subsets[i].parent);
}
return subsets[i].parent;
}
// A function that does union of two sets of x and y
// (uses union by rank)
public static void Union(subset subsets[], int x, int y)
{
int xroot = find(subsets, x);
int yroot = find(subsets, y);
// Attach smaller rank tree under root of high
// rank tree (Union by Rank)
if (subsets[xroot].rank < subsets[yroot].rank) {
subsets[xroot].parent = yroot;
}
else {
if (subsets[xroot].rank > subsets[yroot].rank) {
subsets[yroot].parent = xroot;
}
// If ranks are same, then make one as root and
// increment its rank by one
else {
subsets[yroot].parent = xroot;
subsets[xroot].rank++;
}
}
}
// Driver program to test above functions
public static void main(String[] args)
{
/* Let us create following unweighted graph
0------1
| \ |
| \ |
| \|
2------3 */
int V = 4; // Number of vertices in graph
int E = 5; // Number of edges in graph
// Creates a graph with V vertices and E edges
Graph graph = new Graph(V, E);
// add edge 0-1
graph.edge[0] = new Edge(0, 1);
// add edge 0-2
graph.edge[1] = new Edge(0, 2);
// add edge 0-3
graph.edge[2] = new Edge(0, 3);
// add edge 1-3
graph.edge[3] = new Edge(1, 3);
// add edge 2-3
graph.edge[4] = new Edge(2, 3);
System.out.println(
"Cut found by Karger's randomized algo is "
+ kargerMinCut(graph));
}
}
// This code is contributed by shruti456rawal
# Karger's algorithm to find Minimum Cut in an
# undirected, unweighted and connected graph.
import random
# a class to represent a unweighted edge in graph
class Edge:
def __init__(self, s, d):
self.src = s
self.dest = d
# a class to represent a connected, undirected
# and unweighted graph as a collection of edges.
class Graph:
# V-> Number of vertices, E-> Number of edges
def __init__(self, v, e):
self.V = v
self.E = e
# graph is represented as an array of edges.
# Since the graph is undirected, the edge
# from src to dest is also edge from dest
# to src. Both are counted as 1 edge here.
self.edge = []
# A class to represent a subset for union-find
class subset:
def __init__(self, p, r):
self.parent = p
self.rank = r
# A very basic implementation of Karger's randomized
# algorithm for finding the minimum cut. Please note
# that Karger's algorithm is a Monte Carlo Randomized algo
# and the cut returned by the algorithm may not be
# minimum always
def kargerMinCut(graph):
# Get data of given graph
V = graph.V
E = graph.E
edge = graph.edge
# Allocate memory for creating V subsets.
subsets = []
# Create V subsets with single elements
for v in range(V):
subsets.append(subset(v, 0))
# Initially there are V vertices in
# contracted graph
vertices = V
# Keep contracting vertices until there are
# 2 vertices.
while vertices > 2:
# Pick a random edge
i = int(10 * random.random()) % E
# Find vertices (or sets) of two corners
# of current edge
subset1 = find(subsets, edge[i].src)
subset2 = find(subsets, edge[i].dest)
# If two corners belong to same subset,
# then no point considering this edge
if subset1 == subset2:
continue
# Else contract the edge (or combine the
# corners of edge into one vertex)
else:
print("Contracting edge " +
str(edge[i].src) + "-" + str(edge[i].dest))
vertices -= 1
Union(subsets, subset1, subset2)
# Now we have two vertices (or subsets) left in
# the contracted graph, so count the edges between
# two components and return the count.
cutedges = 0
for i in range(E):
subset1 = find(subsets, edge[i].src)
subset2 = find(subsets, edge[i].dest)
if subset1 != subset2:
cutedges += 1
return cutedges
# A utility function to find set of an element i
# (uses path compression technique)
def find(subsets, i):
# find root and make root as parent of i
# (path compression)
if subsets[i].parent != i:
subsets[i].parent = find(subsets, subsets[i].parent)
return subsets[i].parent
# A function that does union of two sets of x and y
# (uses union by rank)
def Union(subsets, x, y):
xroot = find(subsets, x)
yroot = find(subsets, y)
# Attach smaller rank tree under root of high
# rank tree (Union by Rank)
if subsets[xroot].rank < subsets[yroot].rank:
subsets[xroot].parent = yroot
elif subsets[xroot].rank > subsets[yroot].rank:
subsets[yroot].parent = xroot
# If ranks are same, then make one as root and
# increment its rank by one
else:
subsets[yroot].parent = xroot
subsets[xroot].rank += 1
# Driver program to test above functions
def main():
# Let us create following unweighted graph
# 0------1
# | \ |
# | \ |
# | \ |
# | \ |
# 3------2
V = 4
E = 5
graph = Graph(V, E)
# add edge 0-1
graph.edge.append(Edge(0, 1))
# add edge 0-2
graph.edge.append(Edge(0, 2))
# add edge 0-3
graph.edge.append(Edge(0, 3))
# add edge 1-2
graph.edge.append(Edge(1, 2))
# add edge 2-3
graph.edge.append(Edge(2, 3))
r = random.random()
res = kargerMinCut(graph)
print("Cut found by Karger's randomized algo is", res)
if __name__ == '__main__':
main()
using System;
using System.IO;
using System.Collections.Generic;
class GFG {
// a structure to represent a unweighted edge in graph
public class Edge {
public int src, dest;
public Edge(int s, int d)
{
this.src = s;
this.dest = d;
}
}
// a structure to represent a connected, undirected
// and unweighted graph as a collection of edges.
public class Graph {
// V-> Number of vertices, E-> Number of edges
public int V, E;
// graph is represented as an array of edges.
// Since the graph is undirected, the edge
// from src to dest is also edge from dest
// to src. Both are counted as 1 edge here.
public Edge[] edge;
public Graph(int v, int e)
{
this.V = v;
this.E = e;
this.edge = new Edge[e];
}
}
// A structure to represent a subset for union-find
public class subset {
public int parent;
public int rank;
public subset(int p, int r)
{
this.parent = p;
this.rank = r;
}
}
// A very basic implementation of Karger's randomized
// algorithm for finding the minimum cut. Please note
// that Karger's algorithm is a Monte Carlo Randomized
// algo and the cut returned by the algorithm may not be
// minimum always
public static int kargerMinCut(Graph graph)
{
// Get data of given graph
int V = graph.V, E = graph.E;
Edge[] edge = graph.edge;
// Allocate memory for creating V subsets.
subset[] subsets = new subset[V];
// Create V subsets with single elements
for (int v = 0; v < V; ++v) {
subsets[v] = new subset(v, 0);
}
// Initially there are V vertices in
// contracted graph
int vertices = V;
// Keep contracting vertices until there are
// 2 vertices.
while (vertices > 2) {
// Pick a random edge
int i = ((int)(new Random().NextDouble() * 10))
% E;
// Find vertices (or sets) of two corners
// of current edge
int subset1 = find(subsets, edge[i].src);
int subset2 = find(subsets, edge[i].dest);
// If two corners belong to same subset,
// then no point considering this edge
if (subset1 == subset2) {
continue;
}
// Else contract the edge (or combine the
// corners of edge into one vertex)
else {
Console.WriteLine("Contracting edge "
+ edge[i].src + "-"
+ edge[i].dest);
vertices--;
Union(subsets, subset1, subset2);
}
}
// Now we have two vertices (or subsets) left in
// the contracted graph, so count the edges between
// two components and return the count.
int cutedges = 0;
for (int i = 0; i < E; i++) {
int subset1 = find(subsets, edge[i].src);
int subset2 = find(subsets, edge[i].dest);
if (subset1 != subset2) {
cutedges++;
}
}
return cutedges;
}
// A utility function to find set of an element i
// (uses path compression technique)
public static int find(subset[] subsets, int i)
{
// find root and make root as parent of i
// (path compression)
if (subsets[i].parent != i) {
subsets[i].parent
= find(subsets, subsets[i].parent);
}
return subsets[i].parent;
}
// A function that does union of two sets of x and y
// (uses union by rank)
public static void Union(subset[] subsets, int x, int y)
{
int xroot = find(subsets, x);
int yroot = find(subsets, y);
// Attach smaller rank tree under root of high
// rank tree (Union by Rank)
if (subsets[xroot].rank < subsets[yroot].rank) {
subsets[xroot].parent = yroot;
}
else if (subsets[xroot].rank
> subsets[yroot].rank) {
subsets[yroot].parent = xroot;
}
// If ranks are same, then make one as root and
// increment its rank by one
else {
subsets[yroot].parent = xroot;
subsets[xroot].rank++;
}
}
// Driver program to test above functions
public static void Main()
{
// Let us create following unweighted graph
// 0------1
// | \ |
// | \ |
// | \ |
// | \ |
// 3------2
int V = 4, E = 5;
Graph graph = new Graph(V, E);
// add edge 0-1
graph.edge[0] = new Edge(0, 1);
// add edge 0-2
graph.edge[1] = new Edge(0, 2);
// add edge 0-3
graph.edge[2] = new Edge(0, 3);
// add edge 1-2
graph.edge[3] = new Edge(1, 2);
// add edge 2-3
graph.edge[4] = new Edge(2, 3);
// Use a different seed value for every run.
Random r = new Random();
int res = kargerMinCut(graph);
Console.WriteLine(
"Cut found by Karger's randomized algo is "
+ res);
}
} // this code is contributed by devendrasalunke
class Edge {
constructor(s, d) {
this.src = s;
this.dest = d;
}
}
class Graph {
constructor(v, e) {
this.V = v;
this.E = e;
this.edge = [];
}
}
class subset {
constructor(p, r) {
this.parent = p;
this.rank = r;
}
}
function kargerMinCut(graph) {
let V = graph.V;
let E = graph.E;
let edge = graph.edge;
let subsets = [];
for (let v = 0; v < V; v++) {
subsets[v] = new subset(v, 0);
}
let vertices = V;
while (vertices > 2) {
let i = Math.floor(Math.random() * 10) % E;
let subset1 = find(subsets, edge[i].src);
let subset2 = find(subsets, edge[i].dest);
if (subset1 === subset2) {
continue;
} else {
console.log("Contracting edge " + edge[i].src + "-"
+ edge[i].dest);
vertices--;
Union(subsets, subset1, subset2);
}
}
let cutedges = 0;
for (let i = 0; i < E; i++) {
let subset1 = find(subsets, edge[i].src);
let subset2 = find(subsets, edge[i].dest);
if (subset1 !== subset2) {
cutedges++;
}
}
return cutedges;
}
function find(subsets, i) {
if (subsets[i].parent !== i) {
subsets[i].parent = find(subsets, subsets[i].parent);
}
return subsets[i].parent;
}
function Union(subsets, x, y) {
let xroot = find(subsets, x);
let yroot = find(subsets, y);
if (subsets[xroot].rank < subsets[yroot].rank) {
subsets[xroot].parent = yroot;
} else if (subsets[xroot].rank > subsets[yroot].rank) {
subsets[yroot].parent = xroot;
} else {
subsets[yroot].parent = xroot;
subsets[xroot].rank++;
}
}
// Driver program to test above functions
function main() {
// Let us create following unweighted graph
// 0------1
// | \ |
// | \ |
// | \ |
// | \ |
// 3------2
let V = 4, E = 5;
let graph = new Graph(V, E);
// add edge 0-1
graph.edge[0] = new Edge(0, 1);
// add edge 0-2
graph.edge[1] = new Edge(0, 2);
// add edge 0-3
graph.edge[2] = new Edge(0, 3);
// add edge 1-2
graph.edge[3] = new Edge(1, 2);
// add edge 2-3
graph.edge[4] = new Edge(2, 3);
// Use a different seed value for every run.
let r = Math.random();
let res = kargerMinCut(graph);
console.log(
"Cut found by Karger's randomized algo is " + res
);
}
main();
// this code is contributed by writer
OutputContracting edge 0-1
Contracting edge 1-3
Cut found by Karger's randomized algo is 2
Note that the above program is based on outcome of a random function and may produce different output.
In this post, we have discussed simple Karger’s algorithm and have seen that the algorithm doesn’t always produce min-cut. The above algorithm produces min-cut with probability greater or equal to that 1/(n2). See next post on Analysis and Applications of Karger’s Algorithm, applications, proof of this probability and improvements are discussed.
Complexity Analysis :
Time Complexity : O(EV^2), where E is the number of edges and V is the number of vertices in the graph. The algorithm is not guaranteed to always find the minimum cut, but it has a high probability of doing so with a large number of iterations. The time complexity is dominated by the while loop, which runs for V-2 iterations and performs a constant amount of work on each iteration. The work on each iteration includes finding the subset of an element, union of subsets, and contract the edge. So, the time complexity is O(EV^2) where V is number of vertices and E is number of edges.
Auxiliary Space : The Auxiliary Space of the above code is O(E + V), where E is the number of edges in the graph and V is the number of vertices. This is because the program uses an adjacency list to store the graph, which requires O(E) space. It also uses two lists to store visited vertices and the BFS queue, which require O(V) space. In total, the program uses O(E + V) space.
Share your thoughts in the comments
Please Login to comment...