Depth First Search or DFS for a Graph

Depth First Traversal (or DFS) for a graph is similar to Depth First Traversal of a tree. The only catch here is, that, unlike trees, graphs may contain cycles (a node may be visited twice). To avoid processing a node more than once, use a boolean visited array. A graph can have more than one DFS traversal.

Example:

Input: n = 4, e = 6 
0 -> 1, 0 -> 2, 1 -> 2, 2 -> 0, 2 -> 3, 3 -> 3 
Output: DFS from vertex 1 : 1 2 0 3 
Explanation:
DFS Diagram: 

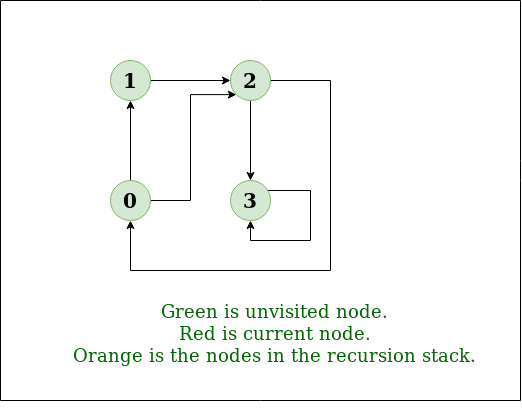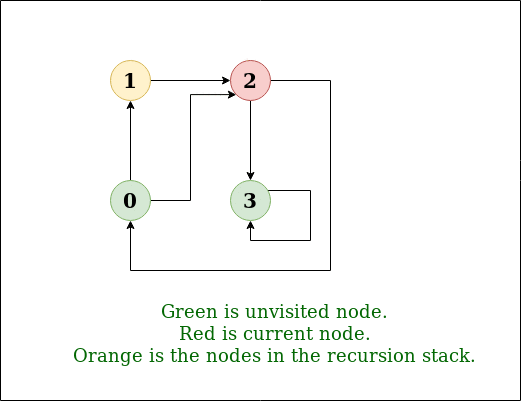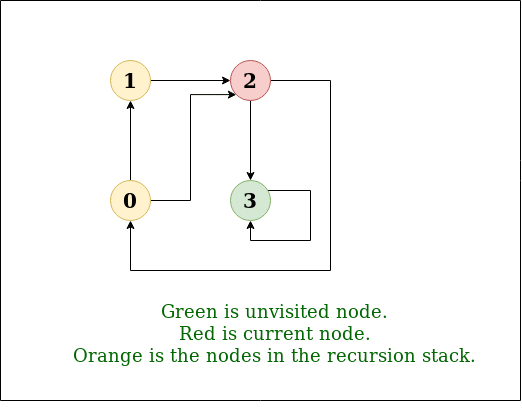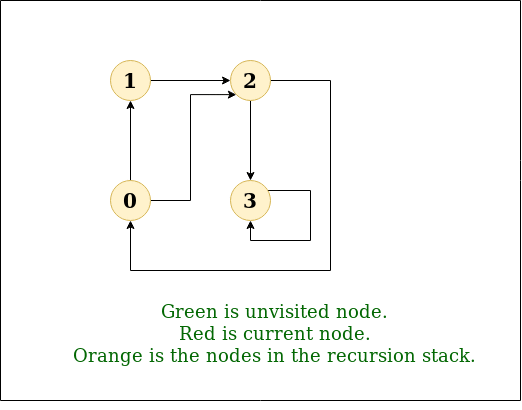
Example 1

Input: n = 4, e = 6 
2 -> 0, 0 -> 2, 1 -> 2, 0 -> 1, 3 -> 3, 1 -> 3 
Output: DFS from vertex 2 : 2 0 1 3 
Explanation:
DFS Diagram: 

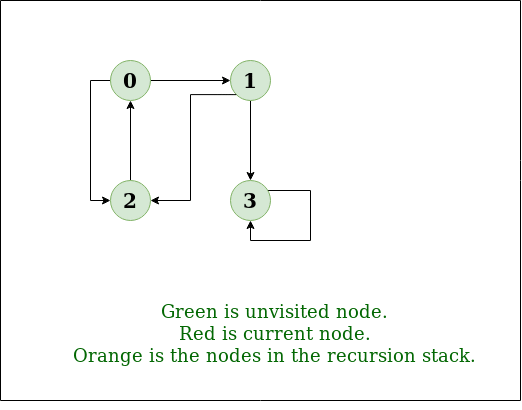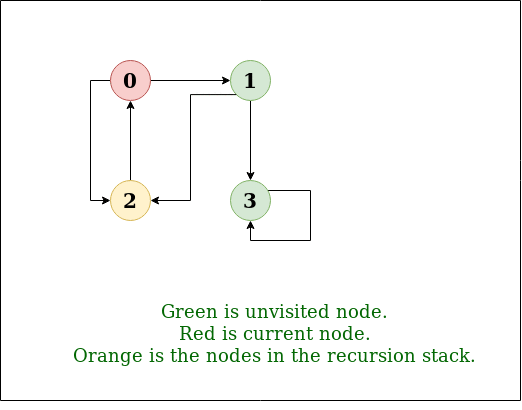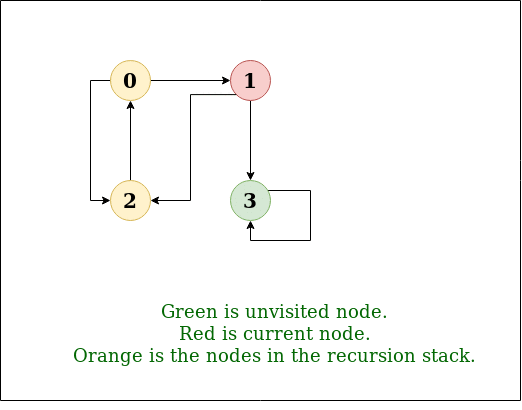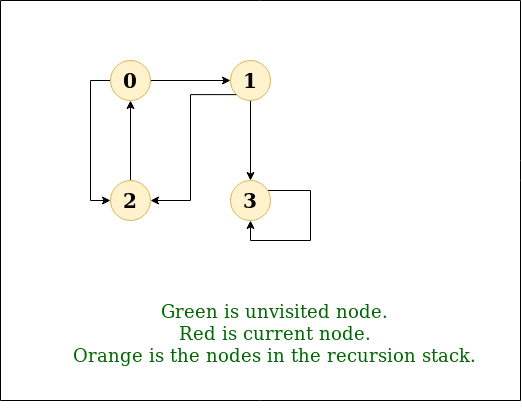
Example 2

Prerequisites:  See this post for all applications of Depth First Traversal.

Depth-first search is an algorithm for traversing or searching tree or graph data structures. The algorithm starts at the root node (selecting some arbitrary node as the root node in the case of a graph) and explores as far as possible along each branch before backtracking. 

So the basic idea is to start from the root or any arbitrary node and mark the node and move to the adjacent unmarked node and continue this loop until there is no unmarked adjacent node. Then backtrack and check for other unmarked nodes and traverse them. Finally, print the nodes in the path.

Implementation of DFS traversal on Graph:

Pseudocode for DFS:

procedure DFS(node):
    mark node as visited
    process(node)
    
    for each neighbor in node.neighbors:
        if neighbor is not visited:
            DFS(neighbor)

Follow the below method to implement DFS traversal.

• Step 1: Create a set or array to keep track of visited nodes.
• Step 2: Choose a starting node.
• Step 3: Create an empty stack and push the starting node onto the stack.
• Step 4: Mark the starting node as visited.
• Step 5: While the stack is not empty, do the following:
  • Pop a node from the stack.
  • Process or perform any necessary operations on the popped node.
  • Get all the adjacent neighbors of the popped node.
  • For each adjacent neighbor, if it has not been visited, do the following:
    • Mark the neighbor as visited.
    • Push the neighbor onto the stack.
• Step 6: Repeat step 5 until the stack is empty.

Illustration:

Step1: Initially stack and visited arrays are empty.

Stack and visited arrays are empty initially.

Step 2: Visit 0 and put its adjacent nodes which are not visited yet into the stack.

 Visit node 0 and put its adjacent nodes (1, 2, 3) into the stack

Step 3: Now, Node 1 at the top of the stack, so visit node 1 and pop it from the stack and put all of its adjacent nodes which are not visited in the stack.

 Visit node 1

Step 4: Now, Node 2 at the top of the stack, so visit node 2 and pop it from the stack and put all of its adjacent nodes which are not visited (i.e, 3, 4) in the stack.

 Visit node 2 and put its unvisited adjacent nodes (3, 4) into the stack

Step 5: Now, Node 4 at the top of the stack, so visit node 4 and pop it from the stack and put all of its adjacent nodes which are not visited in the stack.

 Visit node 4

Step 6: Now, Node 3 at the top of the stack, so visit node 3 and pop it from the stack and put all of its adjacent nodes which are not visited in the stack.

Visit node 3

Now, Stack becomes empty, which means we have visited all the nodes and our DFS traversal ends.

Below is the implementation of the above approach:

C++

// C++ program to print DFS traversal from
// a given vertex in a  given graph
#include <bits/stdc++.h>
using namespace std;

// Graph class represents a directed graph
// using adjacency list representation
class Graph {
public:
    map<int, bool> visited;
    map<int, list<int> > adj;

    // function to add an edge to graph
    void addEdge(int v, int w);

    // DFS traversal of the vertices
    // reachable from v
    void DFS(int v);
};

void Graph::addEdge(int v, int w)
{
    adj[v].push_back(w); // Add w to v’s list.
}

void Graph::DFS(int v)
{
    // Mark the current node as visited and
    // print it
    visited[v] = true;
    cout << v << " ";

    // Recur for all the vertices adjacent
    // to this vertex
    list<int>::iterator i;
    for (i = adj[v].begin(); i != adj[v].end(); ++i)
        if (!visited[*i])
            DFS(*i);
}

// Driver's code
int main()
{
    // Create a graph given in the above diagram
    Graph g;
    g.addEdge(0, 1);
    g.addEdge(0, 2);
    g.addEdge(1, 2);
    g.addEdge(2, 0);
    g.addEdge(2, 3);
    g.addEdge(3, 3);

    cout << "Following is Depth First Traversal"
            " (starting from vertex 2) \n";

    // Function call
    g.DFS(2);

    return 0;
}

// improved by Vishnudev C

Java

// Java program to print DFS
// traversal from a given
// graph
import java.io.*;
import java.util.*;

// This class represents a
// directed graph using adjacency
// list representation
class Graph {
    private int V; // No. of vertices

    // Array  of lists for
    // Adjacency List Representation
    private LinkedList<Integer> adj[];

    // Constructor
    @SuppressWarnings("unchecked") Graph(int v)
    {
        V = v;
        adj = new LinkedList[v];
        for (int i = 0; i < v; ++i)
            adj[i] = new LinkedList();
    }

    // Function to add an edge into the graph
    void addEdge(int v, int w)
    {
        adj[v].add(w); // Add w to v's list.
    }

    // A function used by DFS
    void DFSUtil(int v, boolean visited[])
    {
        // Mark the current node as visited and print it
        visited[v] = true;
        System.out.print(v + " ");

        // Recur for all the vertices adjacent to this
        // vertex
        Iterator<Integer> i = adj[v].listIterator();
        while (i.hasNext()) {
            int n = i.next();
            if (!visited[n])
                DFSUtil(n, visited);
        }
    }

    // The function to do DFS traversal.
    // It uses recursive
    // DFSUtil()
    void DFS(int v)
    {
        // Mark all the vertices as
        // not visited(set as
        // false by default in java)
        boolean visited[] = new boolean[V];

        // Call the recursive helper
        // function to print DFS
        // traversal
        DFSUtil(v, visited);
    }

    // Driver's Code
    public static void main(String args[])
    {
        Graph g = new Graph(4);

        g.addEdge(0, 1);
        g.addEdge(0, 2);
        g.addEdge(1, 2);
        g.addEdge(2, 0);
        g.addEdge(2, 3);
        g.addEdge(3, 3);

        System.out.println(
            "Following is Depth First Traversal "
            + "(starting from vertex 2)");

        // Function call
        g.DFS(2);
    }
}
// This code is contributed by Aakash Hasija

Python3

# Python3 program to print DFS traversal
# from a given  graph
from collections import defaultdict

# This class represents a directed graph using
# adjacency list representation


class Graph:

    # Constructor
    def __init__(self):

        # default dictionary to store graph
        self.graph = defaultdict(list)

    # function to add an edge to graph
    def addEdge(self, u, v):
        self.graph[u].append(v)

    # A function used by DFS
    def DFSUtil(self, v, visited):

        # Mark the current node as visited
        # and print it
        visited.add(v)
        print(v, end=' ')

        # Recur for all the vertices
        # adjacent to this vertex
        for neighbour in self.graph[v]:
            if neighbour not in visited:
                self.DFSUtil(neighbour, visited)

    # The function to do DFS traversal. It uses
    # recursive DFSUtil()
    def DFS(self, v):

        # Create a set to store visited vertices
        visited = set()

        # Call the recursive helper function
        # to print DFS traversal
        self.DFSUtil(v, visited)

# Driver's code


# Create a graph given
# in the above diagram
if __name__ == "__main__":
    g = Graph()
    g.addEdge(0, 1)
    g.addEdge(0, 2)
    g.addEdge(1, 2)
    g.addEdge(2, 0)
    g.addEdge(2, 3)
    g.addEdge(3, 3)

    print("Following is DFS from (starting from vertex 2)")
    # Function call
    g.DFS(2)

# This code is contributed by Neelam Yadav

C#

// C# program to print DFS traversal
// from a given graph
using System;
using System.Collections.Generic;

// This class represents a directed graph
// using adjacency list representation
class Graph {
    private int V; // No. of vertices

    // Array of lists for
    // Adjacency List Representation
    private List<int>[] adj;

    // Constructor
    Graph(int v)
    {
        V = v;
        adj = new List<int>[ v ];
        for (int i = 0; i < v; ++i)
            adj[i] = new List<int>();
    }

    // Function to Add an edge into the graph
    void AddEdge(int v, int w)
    {
        adj[v].Add(w); // Add w to v's list.
    }

    // A function used by DFS
    void DFSUtil(int v, bool[] visited)
    {
        // Mark the current node as visited
        // and print it
        visited[v] = true;
        Console.Write(v + " ");

        // Recur for all the vertices
        // adjacent to this vertex
        List<int> vList = adj[v];
        foreach(var n in vList)
        {
            if (!visited[n])
                DFSUtil(n, visited);
        }
    }

    // The function to do DFS traversal.
    // It uses recursive DFSUtil()
    void DFS(int v)
    {
        // Mark all the vertices as not visited
        // (set as false by default in c#)
        bool[] visited = new bool[V];

        // Call the recursive helper function
        // to print DFS traversal
        DFSUtil(v, visited);
    }

    // Driver's Code
    public static void Main(String[] args)
    {
        Graph g = new Graph(4);

        g.AddEdge(0, 1);
        g.AddEdge(0, 2);
        g.AddEdge(1, 2);
        g.AddEdge(2, 0);
        g.AddEdge(2, 3);
        g.AddEdge(3, 3);

        Console.WriteLine(
            "Following is Depth First Traversal "
            + "(starting from vertex 2)");

        // Function call
        g.DFS(2);
        Console.ReadKey();
    }
}

// This code is contributed by techno2mahi

Javascript

// Javascript program to print DFS
// traversal from a given
// graph

// This class represents a
// directed graph using adjacency
// list representation
class Graph
{

    // Constructor
    constructor(v)
    {
        this.V = v;
        this.adj = new Array(v);
        for(let i = 0; i < v; i++)
            this.adj[i] = [];
    }

    // Function to add an edge into the graph
    addEdge(v, w)
    {

        // Add w to v's list.
        this.adj[v].push(w);
    }

    // A function used by DFS
    DFSUtil(v, visited)
    {

        // Mark the current node as visited and print it
        visited[v] = true;
        document.write(v + " ");

        // Recur for all the vertices adjacent to this
        // vertex
        for(let i of this.adj[v].values())
        {
            let n = i
            if (!visited[n])
                this.DFSUtil(n, visited);
        }
    }

    // The function to do DFS traversal.
    // It uses recursive
    // DFSUtil()
    DFS(v)
    {

        // Mark all the vertices as
        // not visited(set as
        // false by default in java)
        let visited = new Array(this.V);
        for(let i = 0; i < this.V; i++)
            visited[i] = false;

        // Call the recursive helper
        // function to print DFS
        // traversal
        this.DFSUtil(v, visited);
    }
}

// Driver Code
g = new Graph(4);

g.addEdge(0, 1);
g.addEdge(0, 2);
g.addEdge(1, 2);
g.addEdge(2, 0);
g.addEdge(2, 3);
g.addEdge(3, 3);

document.write("Following is Depth First Traversal " +
               "(starting from vertex 2)<br>");

g.DFS(2);

// This code is contributed by avanitrachhadiya2155

Output

Following is Depth First Traversal (starting from vertex 2) 
2 0 1 3 

Time complexity: O(V + E), where V is the number of vertices and E is the number of edges in the graph.
Auxiliary Space: O(V + E), since an extra visited array of size V is required, And stack size for iterative call to DFS function.

Handling A Disconnected Graph:

This will happen by handling a corner case. 

The above code traverses only the vertices reachable from a given source vertex. All the vertices may not be reachable from a given vertex, as in a Disconnected graph. To do a complete DFS traversal of such graphs, run DFS from all unvisited nodes after a DFS. The recursive function remains the same.

Follow the below steps to solve the problem:

• Create a recursive function that takes the index of the node and a visited array.
• Mark the current node as visited and print the node.
• Traverse all the adjacent and unmarked nodes and call the recursive function with the index of the adjacent node.
• Run a loop from 0 to the number of vertices and check if the node is unvisited in the previous DFS, then call the recursive function with the current node.

Below is the implementation of the above approach:

C++

// C++ program to print DFS
// traversal for a given
// graph
#include <bits/stdc++.h>
using namespace std;

class Graph {

    // A function used by DFS
    void DFSUtil(int v);

public:
    map<int, bool> visited;
    map<int, list<int> > adj;
    // function to add an edge to graph
    void addEdge(int v, int w);

    // prints DFS traversal of the complete graph
    void DFS();
};

void Graph::addEdge(int v, int w)
{
    adj[v].push_back(w); // Add w to v’s list.
}

void Graph::DFSUtil(int v)
{
    // Mark the current node as visited and print it
    visited[v] = true;
    cout << v << " ";

    // Recur for all the vertices adjacent to this vertex
    list<int>::iterator i;
    for (i = adj[v].begin(); i != adj[v].end(); ++i)
        if (!visited[*i])
            DFSUtil(*i);
}

// The function to do DFS traversal. It uses recursive
// DFSUtil()
void Graph::DFS()
{
    // Call the recursive helper function to print DFS
    // traversal starting from all vertices one by one
    for (auto i : adj)
        if (visited[i.first] == false)
            DFSUtil(i.first);
}

// Driver's  Code
int main()
{
    // Create a graph given in the above diagram
    Graph g;
    g.addEdge(0, 1);
    g.addEdge(0, 2);
    g.addEdge(1, 2);
    g.addEdge(2, 0);
    g.addEdge(2, 3);
    g.addEdge(3, 3);

    cout << "Following is Depth First Traversal \n";

    // Function call
    g.DFS();

    return 0;
}
// Improved By Priyank Namdeo

Java

// Java program to print DFS
// traversal from a given
// graph
import java.io.*;
import java.util.*;

// This class represents a
// directed graph using adjacency
// list representation
class Graph {
    private int V; // No. of vertices

    // Array  of lists for
    // Adjacency List Representation
    private LinkedList<Integer> adj[];

    // Constructor
    @SuppressWarnings("unchecked") Graph(int v)
    {
        V = v;
        adj = new LinkedList[v];
        for (int i = 0; i < v; ++i)
            adj[i] = new LinkedList();
    }

    // Function to add an edge into the graph
    void addEdge(int v, int w)
    {
        adj[v].add(w); // Add w to v's list.
    }

    // A function used by DFS
    void DFSUtil(int v, boolean visited[])
    {
        // Mark the current node as visited and print it
        visited[v] = true;
        System.out.print(v + " ");

        // Recur for all the vertices adjacent to this
        // vertex
        Iterator<Integer> i = adj[v].listIterator();
        while (i.hasNext()) {
            int n = i.next();
            if (!visited[n])
                DFSUtil(n, visited);
        }
    }

    // The function to do DFS traversal. It uses recursive
    // DFSUtil()
    void DFS()
    {
        // Mark all the vertices as not visited(set as
        // false by default in java)
        boolean visited[] = new boolean[V];

        // Call the recursive helper function to print DFS
        // traversal starting from all vertices one by one
        for (int i = 0; i < V; ++i)
            if (visited[i] == false)
                DFSUtil(i, visited);
    }

    // Driver's Code
    public static void main(String args[])
    {
        Graph g = new Graph(4);

        g.addEdge(0, 1);
        g.addEdge(0, 2);
        g.addEdge(1, 2);
        g.addEdge(2, 0);
        g.addEdge(2, 3);
        g.addEdge(3, 3);

        System.out.println(
            "Following is Depth First Traversal");

        // Function call
        g.DFS();
    }
}
// This code is contributed by Aakash Hasija

Python3

'''Python3 program to print DFS traversal for complete graph'''
from collections import defaultdict

# this class represents a directed graph using adjacency list representation


class Graph:
    # Constructor
    def __init__(self):
        # default dictionary to store graph
        self.graph = defaultdict(list)

    # Function to add an edge to graph
    def addEdge(self, u, v):
        self.graph[u].append(v)
    # A function used by DFS

    def DFSUtil(self, v, visited):
        # Mark the current node as visited and print it
        visited.add(v)
        print(v, end=" ")

    # recur for all the vertices adjacent to this vertex
        for neighbour in self.graph[v]:
            if neighbour not in visited:
                self.DFSUtil(neighbour, visited)
    # The function to do DFS traversal. It uses recursive DFSUtil

    def DFS(self):
        # create a set to store all visited vertices
        visited = set()
    # call the recursive helper function to print DFS traversal starting from all
    # vertices one by one
        for vertex in self.graph:
            if vertex not in visited:
                self.DFSUtil(vertex, visited)
# Driver's code
# create a graph given in the above diagram


if __name__ == "__main__":
    print("Following is Depth First Traversal \n")
    g = Graph()
    g.addEdge(0, 1)
    g.addEdge(0, 2)
    g.addEdge(1, 2)
    g.addEdge(2, 0)
    g.addEdge(2, 3)
    g.addEdge(3, 3)

    # Function call
    g.DFS()

# This code is contributed by Priyank Namdeo

C#

// C# program to print DFS
// traversal from a given
// graph
using System;
using System.Collections.Generic;

// This class represents a
// directed graph using adjacency
// list representation
public class Graph {
    private int V; // No. of vertices

    // Array of lists for
    // Adjacency List Representation
    private List<int>[] adj;

    // Constructor
    Graph(int v)
    {
        V = v;
        adj = new List<int>[ v ];
        for (int i = 0; i < v; ++i)
            adj[i] = new List<int>();
    }

    // Function to add an edge into the graph
    void addEdge(int v, int w)
    {
        adj[v].Add(w); // Add w to v's list.
    }

    // A function used by DFS
    void DFSUtil(int v, bool[] visited)
    {
        // Mark the current
        // node as visited and print it
        visited[v] = true;
        Console.Write(v + " ");

        // Recur for all the
        // vertices adjacent to this
        // vertex
        foreach(int i in adj[v])
        {
            int n = i;
            if (!visited[n])
                DFSUtil(n, visited);
        }
    }

    // The function to do
    // DFS traversal. It uses recursive
    // DFSUtil()
    void DFS()
    {
        // Mark all the vertices as not visited(set as
        // false by default in java)
        bool[] visited = new bool[V];

        // Call the recursive helper
        // function to print DFS
        // traversal starting from
        // all vertices one by one
        for (int i = 0; i < V; ++i)
            if (visited[i] == false)
                DFSUtil(i, visited);
    }

    // Driver's code
    public static void Main(String[] args)
    {
        Graph g = new Graph(4);

        g.addEdge(0, 1);
        g.addEdge(0, 2);
        g.addEdge(1, 2);
        g.addEdge(2, 0);
        g.addEdge(2, 3);
        g.addEdge(3, 3);

        Console.WriteLine(
            "Following is Depth First Traversal");

        // Function call
        g.DFS();
    }
}

// This code is contributed by PrinciRaj1992

Javascript

// JavaScript program to print DFS
      // traversal from a given
      // graph

      // This class represents a
      // directed graph using adjacency
      // list representation
      class Graph
      {

        // Constructor
        constructor(v) {
          this.V = v;
          this.adj = new Array(v).fill([]);
        }

        // Function to Add an edge into the graph
        AddEdge(v, w) {
          this.adj[v].push(w); // Add w to v's list.
        }

        // A function used by DFS
        DFSUtil(v, visited)
        {

          // Mark the current
          // node as visited and print it
          visited[v] = true;
          document.write(v + " ");

          // Recur for all the
          // vertices adjacent to this
          // vertex
          for (const n of this.adj[v]) {
            if (!visited[n]) this.DFSUtil(n, visited);
          }
        }

        // The function to do
        // DFS traversal. It uses recursive
        // DFSUtil()
        DFS()
        {

          // Mark all the vertices as not visited(set as
          var visited = new Array(this.V).fill(false);

          // Call the recursive helper
          // function to print DFS
          // traversal starting from
          // all vertices one by one
          for (var i = 0; i < this.V; ++i)
            if (visited[i] == false) this.DFSUtil(i, visited);
        }
      }

      // Driver Code
      var g = new Graph(4);

      g.AddEdge(0, 1);
      g.AddEdge(0, 2);
      g.AddEdge(1, 2);
      g.AddEdge(2, 0);
      g.AddEdge(2, 3);
      g.AddEdge(3, 3);

      document.write("Following is Depth First Traversal<br>");

      g.DFS();

      // This code is contributed by rdtank.

Output

Following is Depth First Traversal 
0 1 2 3 

Time complexity: O(V + E), where V is the number of vertices and E is the number of edges in the graph.
Auxiliary Space: O(V), since an extra visited array of size V is required.

Advantages of Depth First Search:

• Memory requirement is only linear with respect to the search graph. This is in contrast with breadth-first search which requires more space. The reason is that the algorithm only needs to store a stack of nodes on the path from the root to the current node.
• The time complexity of a depth-first Search to depth d and branching factor b (the number of children at each node, the outdegree) is O(bd) since it generates the same set of nodes as breadth-first search, but simply in a different order. Thus practically depth-first search is time-limited rather than space-limited.
•  If depth-first search finds solution without exploring much in a path then the time and space it takes will be very less.
• DFS requires less memory since only the nodes on the current path are stored. By chance DFS may find a solution without examining much of the search space at all.

Disadvantages of Depth First Search:

• The disadvantage of Depth-First Search is that there is a possibility that it may down the left-most path forever. Even a finite graph can generate an infinite tre One solution to this problem is to impose a cutoff depth on the search. Although ideal cutoff is the solution depth d and this value is rarely known in advance of actually solving the problem. If the chosen cutoff depth is less than d, the algorithm will fail to find a solution, whereas if the cutoff depth is greater than d, a large price is paid in execution time, and the first solution found may not be an optimal one.
•  Depth-First Search is not guaranteed to find the solution.
•  And there is no guarantee to find a minimal solution, if more than one solution.

Applications of DFS.

Breadth-First Traversal for a Graph

Recent Articles on DFS

Would you please write comments if you find anything incorrect or share more information about the topic discussed above?