Articulation Points (or Cut Vertices) in a Graph
Last Updated :
17 Apr, 2024
A vertex v is an articulation point (also called cut vertex) if removing v increases the number of connected components.
Articulation points represent vulnerabilities in a connected network – single points whose failure would split the network into 2 or more components. They are useful for designing reliable networks.
Examples:
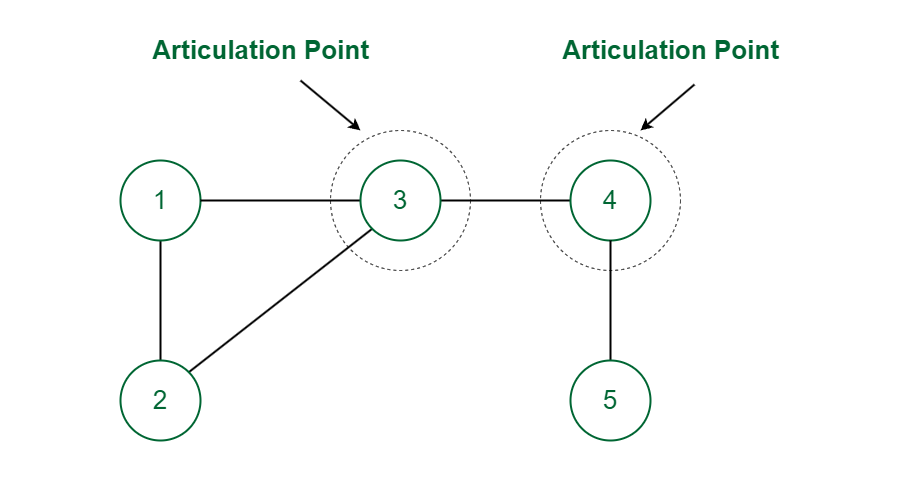
Articulation Point
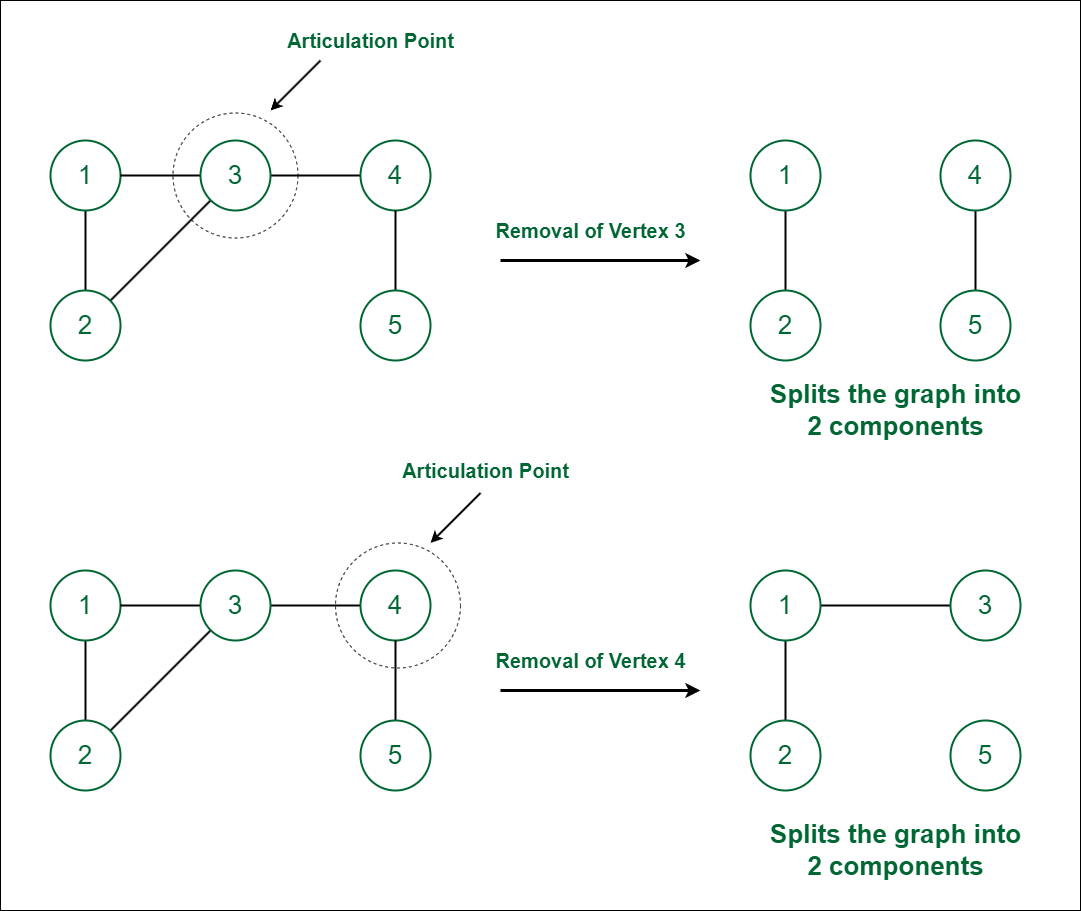
In the above graph vertex 3 and 4 are Articulation Points since the removal of vertex 3 (or 4) along with its associated edges makes the graph disconnected.
Naive approach to find Articulation Points (or Cut Vertices) in a Graph:
A simple approach is to one by one remove all vertices and see if removal of a vertex causes disconnected graph.
Following the below steps to Implement the idea:
- Iterate over all the vertices and for every vertex do the following:
- Remove v from graph
- See if the graph remains connected (We can either use BFS or DFS)
- Add v back to the graph
Below is the implementation of above approach:
C++
// C++ program to find articulation points in an undirected
// graph
#include <bits/stdc++.h>
using namespace std;
// A recursive function to traverse the graph without
// considering the ith vertex and its associated edges
void dfs(vector<int> adj[], int V, vector<int>& vis,
int i, int curr)
{
vis[curr] = 1;
for (auto x : adj[curr]) {
if (x != i) {
if (!vis[x]) {
dfs(adj, V, vis, i, x);
}
}
}
}
// Function to find Articulation Points in the graph
void AP(vector<int> adj[], int V)
{
// Iterating over all the vertices and for each vertex i
// remove the vertex and check whether the graph remains
// connected.
for (int i = 1; i <= V; i++) {
// To keep track of number of components of graph
int components = 0;
// To keep track of visited vertices
vector<int> vis(V + 1, 0);
// Iterating over the graph after removing vertex i
// and its associated edges
for (int j = 1; j <= V; j++) {
if (j != i) {
// If the jth vertex is not visited it will
// form a new component.
if (!vis[j]) {
// Increasing the number of components.
components++;
// dfs call for the jth vertex
dfs(adj, V, vis, i, j);
}
}
}
// If number of components is more than 1 after
// removing the ith vertex then vertex i is an
// articulation point.
if (components > 1) {
cout << i << "\n";
}
}
}
// Utility function to add an edge
void addEdge(vector<int> adj[], int u, int v)
{
adj[u].push_back(v);
adj[v].push_back(u);
}
// Driver Code
int main()
{
// Create graphs given in above diagrams
cout << "Articulation points in the graph \n";
int V = 5;
vector<int> adj1[V + 1];
addEdge(adj1, 1, 2);
addEdge(adj1, 2, 3);
addEdge(adj1, 1, 3);
addEdge(adj1, 3, 4);
addEdge(adj1, 4, 5);
AP(adj1, V);
return 0;
}
import java.util.ArrayList;
import java.util.List;
public class GFG {
// A recursive function to traverse the graph without
// considering the ith vertex and its associated edges
static void dfs(List<Integer>[] adj, int V, List<Integer> vis,
int i, int curr) {
vis.set(curr, 1);
for (int x : adj[curr]) {
if (x != i) {
if (vis.get(x) == 0) {
dfs(adj, V, vis, i, x);
}
}
}
}
// Function to find Articulation Points in the graph
static void AP(List<Integer>[] adj, int V) {
// Iterating over all the vertices and for each vertex i
// remove the vertex and check whether the graph remains
// connected.
for (int i = 1; i <= V; i++) {
// To keep track of number of components of graph
int components = 0;
// To keep track of visited vertices
List<Integer> vis = new ArrayList<>();
for (int j = 0; j <= V; j++) {
vis.add(0);
}
// Iterating over the graph after removing vertex i
// and its associated edges
for (int j = 1; j <= V; j++) {
if (j != i) {
// If the jth vertex is not visited it will
// form a new component.
if (vis.get(j) == 0) {
// Increasing the number of components.
components++;
// dfs call for the jth vertex
dfs(adj, V, vis, i, j);
}
}
}
// If number of components is more than 1 after
// removing the ith vertex then vertex i is an
// articulation point.
if (components > 1) {
System.out.println(i);
}
}
}
// Utility function to add an edge
static void addEdge(List<Integer>[] adj, int u, int v) {
adj[u].add(v);
adj[v].add(u);
}
// Driver Code
public static void main(String[] args) {
// Create graphs given in above diagrams
System.out.println("Articulation points in the graph ");
int V = 5;
List<Integer>[] adj1 = new ArrayList[V + 1];
for (int i = 0; i <= V; i++) {
adj1[i] = new ArrayList<>();
}
addEdge(adj1, 1, 2);
addEdge(adj1, 2, 3);
addEdge(adj1, 1, 3);
addEdge(adj1, 3, 4);
addEdge(adj1, 4, 5);
AP(adj1, V);
}
}
// This code is contributed by shivamgupta310570
# A recursive function to traverse the graph without
# considering the ith vertex and its associated edges
def dfs(adj, V, vis, i, curr):
vis[curr] = 1
for x in adj[curr]:
if x != i and not vis[x]:
dfs(adj, V, vis, i, x)
# Function to find Articulation Points in the graph
def AP(adj, V):
for i in range(1, V + 1):
# To keep track of number of components of graph
components = 0
# To keep track of visited vertices
vis = [0] * (V + 1)
# Iterating over the graph after removing vertex i
# and its associated edges
for j in range(1, V + 1):
if j != i:
# If the jth vertex is not visited, it will
# form a new component.
if not vis[j]:
# Increasing the number of components.
components += 1
# dfs call for the jth vertex
dfs(adj, V, vis, i, j)
# If number of components is more than 1 after
# removing the ith vertex then vertex i is an
# articulation point.
if components > 1:
print(i)
# Utility function to add an edge
def addEdge(adj, u, v):
adj[u].append(v)
adj[v].append(u)
# Driver Code
if __name__ == "__main__":
# Create graphs given in above diagrams
print("Articulation points in the graph")
V = 5
adj1 = [[] for _ in range(V + 1)]
addEdge(adj1, 1, 2)
addEdge(adj1, 2, 3)
addEdge(adj1, 1, 3)
addEdge(adj1, 3, 4)
addEdge(adj1, 4, 5)
AP(adj1, V)
# This code is contributed by shivamgupta310570
using System;
using System.Collections.Generic;
class Program {
// A recursive function to traverse the graph without
// considering the ith vertex and its associated edges
static void Dfs(List<int>[] adj, int V, int[] vis,
int i, int curr)
{
vis[curr] = 1;
foreach(var x in adj[curr])
{
if (x != i) {
if (vis[x] == 0) {
Dfs(adj, V, vis, i, x);
}
}
}
}
// Function to find Articulation Points in the graph
static void AP(List<int>[] adj, int V)
{
// Iterating over all the vertices and for each
// vertex i remove the vertex and check whether the
// graph remains connected.
for (int i = 1; i <= V; i++) {
// To keep track of number of components of
// graph
int components = 0;
// To keep track of visited vertices
int[] vis = new int[V + 1];
// Iterating over the graph after removing
// vertex i and its associated edges
for (int j = 1; j <= V; j++) {
if (j != i) {
// If the jth vertex is not visited it
// will form a new component.
if (vis[j] == 0) {
// Increasing the number of
// components.
components++;
// dfs call for the jth vertex
Dfs(adj, V, vis, i, j);
}
}
}
// If the number of components is more than 1
// after removing the ith vertex, then vertex i
// is an articulation point.
if (components > 1) {
Console.WriteLine(i);
}
}
}
// Utility function to add an edge
static void AddEdge(List<int>[] adj, int u, int v)
{
adj[u].Add(v);
adj[v].Add(u);
}
// Driver Code
static void Main()
{
// Create graphs given in above diagrams
Console.WriteLine(
"Articulation points in the graph:");
int V = 5;
List<int>[] adj1 = new List<int>[ V + 1 ];
for (int i = 0; i <= V; i++) {
adj1[i] = new List<int>();
}
AddEdge(adj1, 1, 2);
AddEdge(adj1, 2, 3);
AddEdge(adj1, 1, 3);
AddEdge(adj1, 3, 4);
AddEdge(adj1, 4, 5);
AP(adj1, V);
}
}
// A recursive function to traverse the graph without
// considering the ith vertex and its associated edges
function dfs(adj, V, vis, i, curr) {
vis[curr] = 1;
for (let x of adj[curr]) {
if (x !== i) {
if (!vis[x]) {
dfs(adj, V, vis, i, x);
}
}
}
}
// Function to find Articulation Points in the graph
function findArticulationPoints(adj, V) {
for (let i = 1; i <= V; i++) {
let components = 0;
const vis = new Array(V + 1).fill(0);
for (let j = 1; j <= V; j++) {
if (j !== i) {
if (!vis[j]) {
components++;
dfs(adj, V, vis, i, j);
}
}
}
if (components > 1) {
console.log(i);
}
}
}
// Utility function to add an edge
function addEdge(adj, u, v) {
adj[u].push(v);
adj[v].push(u);
}
// Driver Code
console.log("Articulation points in the graph");
const V = 5;
const adj1 = new Array(V + 1).fill().map(() => []);
addEdge(adj1, 1, 2);
addEdge(adj1, 2, 3);
addEdge(adj1, 1, 3);
addEdge(adj1, 3, 4);
addEdge(adj1, 4, 5);
findArticulationPoints(adj1, V);
// This code is contributed by shivamgupta310570
OutputArticulation points in the graph
3
4
Time Complexity: O(V*(V+E)) for a graph represented using an adjacency list.
Auxiliary Space: O(V+E)
Finding Articulation Points (or Cut Vertices) in a Graph using Tarjan’s Algorithm:
The idea is to use DFS (Depth First Search). In DFS, follow vertices in a tree form called the DFS tree. In the DFS tree, a vertex u is the parent of another vertex v, if v is discovered by u.
In DFS tree, a vertex u is an articulation point if one of the following two conditions is true.
- u is the root of the DFS tree and it has at least two children.
- u is not the root of the DFS tree and it has a child v such that no vertex in the subtree rooted with v has a back edge to one of the ancestors in DFS tree of u.
Examples:
Let’s consider the following graph:
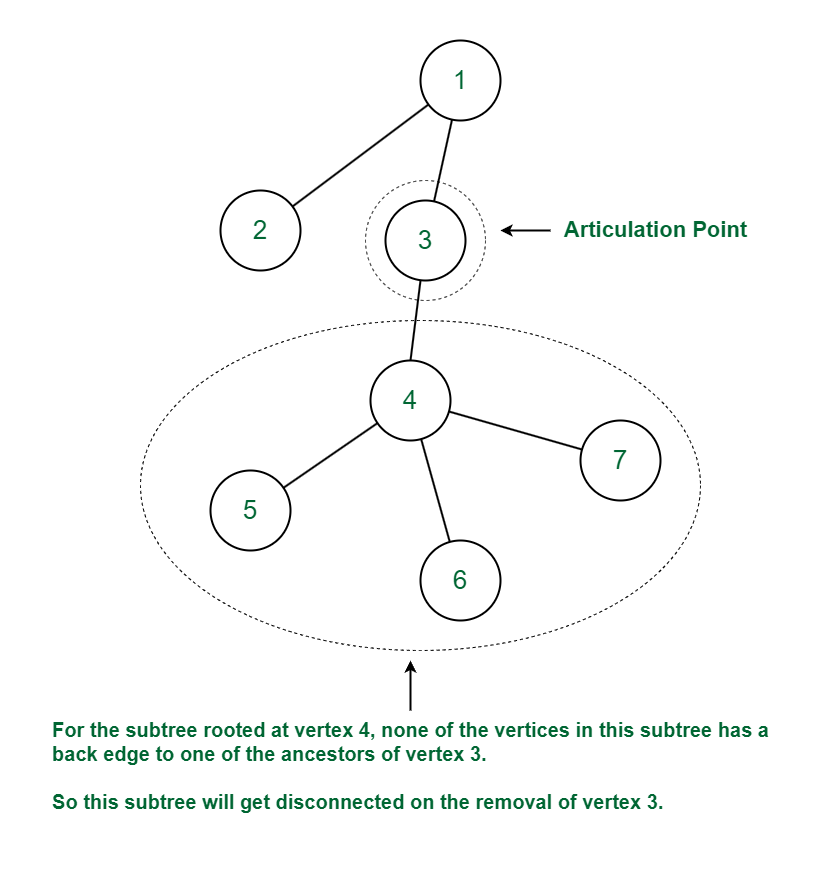
For the vertex 3 (which is not the root), vertex 4 is the child of vertex 3. No vertex in the subtree rooted at vertex 4 has a back edge to one of ancestors of vertex 3. Thus on removal of vertex 3 and its associated edges the graph will get disconnected or the number of components in the graph will increase as the subtree rooted at vertex 4 will form a separate component. Hence vertex 3 is an articulation point.
Now consider the following graph:
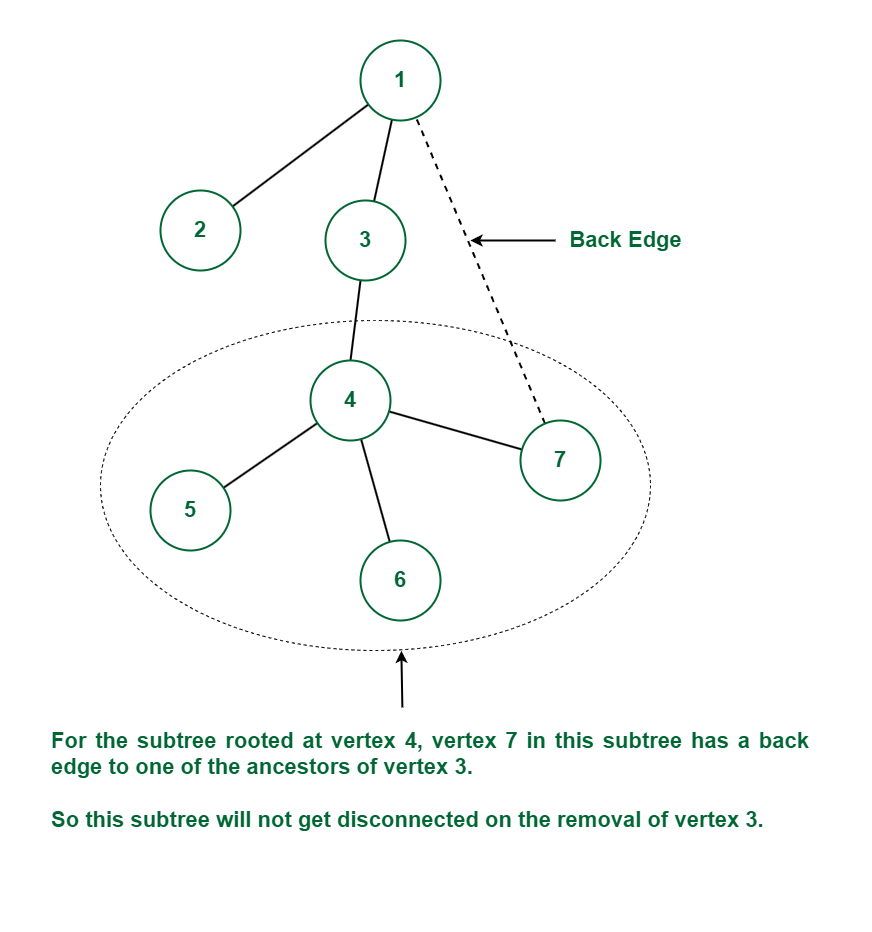
Again the vertex 4 is the child of vertex 3. For the subtree rooted at vertex 4, vertex 7 in this subtree has a back edge to one of the ancestors of vertex 3 (which is vertex 1). Thus this subtree will not get disconnected on the removal of vertex 3 because of this back edge. Since there is no child v of vertex 3, such that subtree rooted at vertex v does not have a back edge to one of the ancestors of vertex 3. Hence vertex 3 is not an articulation point in this case.
Follow the below steps to Implement the idea:
- Do DFS traversal of the given graph
- In DFS traversal, maintain a parent[] array where parent[u] stores the parent of vertex u.
- To check if u is the root of the DFS tree and it has at least two children. For every vertex, count children. If the currently visited vertex u is root (parent[u] is NULL) and has more than two children, print it.
- To handle a second case where u is not the root of the DFS tree and it has a child v such that no vertex in the subtree rooted with v has a back edge to one of the ancestors in DFS tree of u maintain an array disc[] to store the discovery time of vertices.
- For every node u, find out the earliest visited vertex (the vertex with minimum discovery time) that can be reached from the subtree rooted with u. So we maintain an additional array low[] such that:
low[u] = min(disc[u], disc[w]) , Here w is an ancestor of u and there is a back edge from some descendant of u to w.
Below is the Implementation of the above approach:
C++
// C++ program to find articulation points in an undirected graph
#include <bits/stdc++.h>
using namespace std;
// A recursive function that find articulation
// points using DFS traversal
// adj[] --> Adjacency List representation of the graph
// u --> The vertex to be visited next
// visited[] --> keeps track of visited vertices
// disc[] --> Stores discovery times of visited vertices
// low[] -- >> earliest visited vertex (the vertex with minimum
// discovery time) that can be reached from subtree
// rooted with current vertex
// parent --> Stores the parent vertex in DFS tree
// isAP[] --> Stores articulation points
void APUtil(vector<int> adj[], int u, bool visited[],
int disc[], int low[], int& time, int parent,
bool isAP[])
{
// Count of children in DFS Tree
int children = 0;
// Mark the current node as visited
visited[u] = true;
// Initialize discovery time and low value
disc[u] = low[u] = ++time;
// Go through all vertices adjacent to this
for (auto v : adj[u]) {
// If v is not visited yet, then make it a child of u
// in DFS tree and recur for it
if (!visited[v]) {
children++;
APUtil(adj, v, visited, disc, low, time, u, isAP);
// Check if the subtree rooted with v has
// a connection to one of the ancestors of u
low[u] = min(low[u], low[v]);
// If u is not root and low value of one of
// its child is more than discovery value of u.
if (parent != -1 && low[v] >= disc[u])
isAP[u] = true;
}
// Update low value of u for parent function calls.
else if (v != parent)
low[u] = min(low[u], disc[v]);
}
// If u is root of DFS tree and has two or more children.
if (parent == -1 && children > 1)
isAP[u] = true;
}
void AP(vector<int> adj[], int V)
{
int disc[V] = { 0 };
int low[V];
bool visited[V] = { false };
bool isAP[V] = { false };
int time = 0, par = -1;
// Adding this loop so that the
// code works even if we are given
// disconnected graph
for (int u = 0; u < V; u++)
if (!visited[u])
APUtil(adj, u, visited, disc, low,
time, par, isAP);
// Printing the APs
for (int u = 0; u < V; u++)
if (isAP[u] == true)
cout << u << " ";
}
// Utility function to add an edge
void addEdge(vector<int> adj[], int u, int v)
{
adj[u].push_back(v);
adj[v].push_back(u);
}
int main()
{
// Create graphs given in above diagrams
cout << "Articulation points in first graph \n";
int V = 5;
vector<int> adj1[V];
addEdge(adj1, 1, 0);
addEdge(adj1, 0, 2);
addEdge(adj1, 2, 1);
addEdge(adj1, 0, 3);
addEdge(adj1, 3, 4);
AP(adj1, V);
cout << "\nArticulation points in second graph \n";
V = 4;
vector<int> adj2[V];
addEdge(adj2, 0, 1);
addEdge(adj2, 1, 2);
addEdge(adj2, 2, 3);
AP(adj2, V);
cout << "\nArticulation points in third graph \n";
V = 7;
vector<int> adj3[V];
addEdge(adj3, 0, 1);
addEdge(adj3, 1, 2);
addEdge(adj3, 2, 0);
addEdge(adj3, 1, 3);
addEdge(adj3, 1, 4);
addEdge(adj3, 1, 6);
addEdge(adj3, 3, 5);
addEdge(adj3, 4, 5);
AP(adj3, V);
return 0;
}
// A Java program to find articulation
// points in an undirected graph
import java.util.*;
class Graph {
static int time;
static void addEdge(ArrayList<ArrayList<Integer> > adj, int u, int v)
{
adj.get(u).add(v);
adj.get(v).add(u);
}
static void APUtil(ArrayList<ArrayList<Integer> > adj, int u,
boolean visited[], int disc[], int low[],
int parent, boolean isAP[])
{
// Count of children in DFS Tree
int children = 0;
// Mark the current node as visited
visited[u] = true;
// Initialize discovery time and low value
disc[u] = low[u] = ++time;
// Go through all vertices adjacent to this
for (Integer v : adj.get(u)) {
// If v is not visited yet, then make it a child of u
// in DFS tree and recur for it
if (!visited[v]) {
children++;
APUtil(adj, v, visited, disc, low, u, isAP);
// Check if the subtree rooted with v has
// a connection to one of the ancestors of u
low[u] = Math.min(low[u], low[v]);
// If u is not root and low value of one of
// its child is more than discovery value of u.
if (parent != -1 && low[v] >= disc[u])
isAP[u] = true;
}
// Update low value of u for parent function calls.
else if (v != parent)
low[u] = Math.min(low[u], disc[v]);
}
// If u is root of DFS tree and has two or more children.
if (parent == -1 && children > 1)
isAP[u] = true;
}
static void AP(ArrayList<ArrayList<Integer> > adj, int V)
{
boolean[] visited = new boolean[V];
int[] disc = new int[V];
int[] low = new int[V];
boolean[] isAP = new boolean[V];
int time = 0, par = -1;
// Adding this loop so that the
// code works even if we are given
// disconnected graph
for (int u = 0; u < V; u++)
if (visited[u] == false)
APUtil(adj, u, visited, disc, low, par, isAP);
for (int u = 0; u < V; u++)
if (isAP[u] == true)
System.out.print(u + " ");
System.out.println();
}
public static void main(String[] args)
{
// Creating first example graph
int V = 5;
ArrayList<ArrayList<Integer> > adj1 =
new ArrayList<ArrayList<Integer> >(V);
for (int i = 0; i < V; i++)
adj1.add(new ArrayList<Integer>());
addEdge(adj1, 1, 0);
addEdge(adj1, 0, 2);
addEdge(adj1, 2, 1);
addEdge(adj1, 0, 3);
addEdge(adj1, 3, 4);
System.out.println("Articulation points in first graph");
AP(adj1, V);
// Creating second example graph
V = 4;
ArrayList<ArrayList<Integer> > adj2 =
new ArrayList<ArrayList<Integer> >(V);
for (int i = 0; i < V; i++)
adj2.add(new ArrayList<Integer>());
addEdge(adj2, 0, 1);
addEdge(adj2, 1, 2);
addEdge(adj2, 2, 3);
System.out.println("Articulation points in second graph");
AP(adj2, V);
// Creating third example graph
V = 7;
ArrayList<ArrayList<Integer> > adj3 =
new ArrayList<ArrayList<Integer> >(V);
for (int i = 0; i < V; i++)
adj3.add(new ArrayList<Integer>());
addEdge(adj3, 0, 1);
addEdge(adj3, 1, 2);
addEdge(adj3, 2, 0);
addEdge(adj3, 1, 3);
addEdge(adj3, 1, 4);
addEdge(adj3, 1, 6);
addEdge(adj3, 3, 5);
addEdge(adj3, 4, 5);
System.out.println("Articulation points in third graph");
AP(adj3, V);
}
}
# Python program to find articulation points in an undirected graph
from collections import defaultdict
# This class represents an undirected graph
# using adjacency list representation
class Graph:
def __init__(self, vertices):
self.V = vertices # No. of vertices
self.graph = defaultdict(list) # default dictionary to store graph
self.Time = 0
# function to add an edge to graph
def addEdge(self, u, v):
self.graph[u].append(v)
self.graph[v].append(u)
'''A recursive function that find articulation points
using DFS traversal
u --> The vertex to be visited next
visited[] --> keeps track of visited vertices
disc[] --> Stores discovery times of visited vertices
parent[] --> Stores parent vertices in DFS tree
ap[] --> Store articulation points'''
def APUtil(self, u, visited, ap, parent, low, disc):
# Count of children in current node
children = 0
# Mark the current node as visited and print it
visited[u]= True
# Initialize discovery time and low value
disc[u] = self.Time
low[u] = self.Time
self.Time += 1
# Recur for all the vertices adjacent to this vertex
for v in self.graph[u]:
# If v is not visited yet, then make it a child of u
# in DFS tree and recur for it
if visited[v] == False :
parent[v] = u
children += 1
self.APUtil(v, visited, ap, parent, low, disc)
# Check if the subtree rooted with v has a connection to
# one of the ancestors of u
low[u] = min(low[u], low[v])
# u is an articulation point in following cases
# (1) u is root of DFS tree and has two or more children.
if parent[u] == -1 and children > 1:
ap[u] = True
#(2) If u is not root and low value of one of its child is more
# than discovery value of u.
if parent[u] != -1 and low[v] >= disc[u]:
ap[u] = True
# Update low value of u for parent function calls
elif v != parent[u]:
low[u] = min(low[u], disc[v])
# The function to do DFS traversal. It uses recursive APUtil()
def AP(self):
# Mark all the vertices as not visited
# and Initialize parent and visited,
# and ap(articulation point) arrays
visited = [False] * (self.V)
disc = [float("Inf")] * (self.V)
low = [float("Inf")] * (self.V)
parent = [-1] * (self.V)
ap = [False] * (self.V) # To store articulation points
# Call the recursive helper function
# to find articulation points
# in DFS tree rooted with vertex 'i'
for i in range(self.V):
if visited[i] == False:
self.APUtil(i, visited, ap, parent, low, disc)
for index, value in enumerate (ap):
if value == True: print (index,end=" ")
# Create a graph given in the above diagram
g1 = Graph(5)
g1.addEdge(1, 0)
g1.addEdge(0, 2)
g1.addEdge(2, 1)
g1.addEdge(0, 3)
g1.addEdge(3, 4)
print ("\nArticulation points in first graph ")
g1.AP()
g2 = Graph(4)
g2.addEdge(0, 1)
g2.addEdge(1, 2)
g2.addEdge(2, 3)
print ("\nArticulation points in second graph ")
g2.AP()
g3 = Graph (7)
g3.addEdge(0, 1)
g3.addEdge(1, 2)
g3.addEdge(2, 0)
g3.addEdge(1, 3)
g3.addEdge(1, 4)
g3.addEdge(1, 6)
g3.addEdge(3, 5)
g3.addEdge(4, 5)
print ("\nArticulation points in third graph ")
g3.AP()
# This code is contributed by Neelam Yadav
// A C# program to find articulation
// points in an undirected graph
using System;
using System.Collections.Generic;
// This class represents an undirected graph
// using adjacency list representation
public class Graph {
private int V; // No. of vertices
// Array of lists for Adjacency List Representation
private List<int>[] adj;
int time = 0;
static readonly int NIL = -1;
// Constructor
Graph(int v)
{
V = v;
adj = new List<int>[v];
for (int i = 0; i < v; ++i)
adj[i] = new List<int>();
}
// Function to add an edge into the graph
void addEdge(int v, int w)
{
adj[v].Add(w); // Add w to v's list.
adj[w].Add(v); // Add v to w's list
}
// A recursive function that find articulation points using DFS
// u --> The vertex to be visited next
// visited[] --> keeps track of visited vertices
// disc[] --> Stores discovery times of visited vertices
// parent[] --> Stores parent vertices in DFS tree
// ap[] --> Store articulation points
void APUtil(int u, bool[] visited, int[] disc,
int[] low, int[] parent, bool[] ap)
{
// Count of children in DFS Tree
int children = 0;
// Mark the current node as visited
visited[u] = true;
// Initialize discovery time and low value
disc[u] = low[u] = ++time;
// Go through all vertices adjacent to this
foreach(int i in adj[u])
{
int v = i; // v is current adjacent of u
// If v is not visited yet, then make it a child of u
// in DFS tree and recur for it
if (!visited[v]) {
children++;
parent[v] = u;
APUtil(v, visited, disc, low, parent, ap);
// Check if the subtree rooted with v has
// a connection to one of the ancestors of u
low[u] = Math.Min(low[u], low[v]);
// u is an articulation point in following cases
// (1) u is root of DFS tree and has two or more children.
if (parent[u] == NIL && children > 1)
ap[u] = true;
// (2) If u is not root and low value of one of its child
// is more than discovery value of u.
if (parent[u] != NIL && low[v] >= disc[u])
ap[u] = true;
}
// Update low value of u for parent function calls.
else if (v != parent[u])
low[u] = Math.Min(low[u], disc[v]);
}
}
// The function to do DFS traversal.
// It uses recursive function APUtil()
void AP()
{
// Mark all the vertices as not visited
bool[] visited = new bool[V];
int[] disc = new int[V];
int[] low = new int[V];
int[] parent = new int[V];
bool[] ap = new bool[V]; // To store articulation points
// Initialize parent and visited, and
// ap(articulation point) arrays
for (int i = 0; i < V; i++) {
parent[i] = NIL;
visited[i] = false;
ap[i] = false;
}
// Call the recursive helper function to find articulation
// points in DFS tree rooted with vertex 'i'
for (int i = 0; i < V; i++)
if (visited[i] == false)
APUtil(i, visited, disc, low, parent, ap);
// Now ap[] contains articulation points, print them
for (int i = 0; i < V; i++)
if (ap[i] == true)
Console.Write(i + " ");
}
// Driver method
public static void Main(String[] args)
{
// Create graphs given in above diagrams
Console.WriteLine("Articulation points in first graph ");
Graph g1 = new Graph(5);
g1.addEdge(1, 0);
g1.addEdge(0, 2);
g1.addEdge(2, 1);
g1.addEdge(0, 3);
g1.addEdge(3, 4);
g1.AP();
Console.WriteLine();
Console.WriteLine("Articulation points in Second graph");
Graph g2 = new Graph(4);
g2.addEdge(0, 1);
g2.addEdge(1, 2);
g2.addEdge(2, 3);
g2.AP();
Console.WriteLine();
Console.WriteLine("Articulation points in Third graph ");
Graph g3 = new Graph(7);
g3.addEdge(0, 1);
g3.addEdge(1, 2);
g3.addEdge(2, 0);
g3.addEdge(1, 3);
g3.addEdge(1, 4);
g3.addEdge(1, 6);
g3.addEdge(3, 5);
g3.addEdge(4, 5);
g3.AP();
}
}
// This code is contributed by PrinciRaj1992
<script>
// A Javascript program to find articulation points in an undirected graph
// This class represents an undirected graph using adjacency list
// representation
class Graph
{
// Constructor
constructor(v)
{
this.V = v;
this.adj = new Array(v);
this.NIL = -1;
this.time = 0;
for (let i=0; i<v; ++i)
this.adj[i] = [];
}
//Function to add an edge into the graph
addEdge(v, w)
{
this.adj[v].push(w); // Add w to v's list.
this.adj[w].push(v); //Add v to w's list
}
// A recursive function that find articulation points using DFS
// u --> The vertex to be visited next
// visited[] --> keeps track of visited vertices
// disc[] --> Stores discovery times of visited vertices
// parent[] --> Stores parent vertices in DFS tree
// ap[] --> Store articulation points
APUtil(u, visited, disc, low, parent, ap)
{
// Count of children in DFS Tree
let children = 0;
// Mark the current node as visited
visited[u] = true;
// Initialize discovery time and low value
disc[u] = low[u] = ++this.time;
// Go through all vertices adjacent to this
for(let i of this.adj[u])
{
let v = i; // v is current adjacent of u
// If v is not visited yet, then make it a child of u
// in DFS tree and recur for it
if (!visited[v])
{
children++;
parent[v] = u;
this.APUtil(v, visited, disc, low, parent, ap);
// Check if the subtree rooted with v has a connection to
// one of the ancestors of u
low[u] = Math.min(low[u], low[v]);
// u is an articulation point in following cases
// (1) u is root of DFS tree and has two or more children.
if (parent[u] == this.NIL && children > 1)
ap[u] = true;
// (2) If u is not root and low value of one of its child
// is more than discovery value of u.
if (parent[u] != this.NIL && low[v] >= disc[u])
ap[u] = true;
}
// Update low value of u for parent function calls.
else if (v != parent[u])
low[u] = Math.min(low[u], disc[v]);
}
}
// The function to do DFS traversal. It uses recursive function APUtil()
AP()
{
// Mark all the vertices as not visited
let visited = new Array(this.V);
let disc = new Array(this.V);
let low = new Array(this.V);
let parent = new Array(this.V);
let ap = new Array(this.V); // To store articulation points
// Initialize parent and visited, and ap(articulation point)
// arrays
for (let i = 0; i < this.V; i++)
{
parent[i] = this.NIL;
visited[i] = false;
ap[i] = false;
}
// Call the recursive helper function to find articulation
// points in DFS tree rooted with vertex 'i'
for (let i = 0; i < this.V; i++)
if (visited[i] == false)
this.APUtil(i, visited, disc, low, parent, ap);
// Now ap[] contains articulation points, print them
for (let i = 0; i < this.V; i++)
if (ap[i] == true)
document.write(i+" ");
}
}
// Driver method
// Create graphs given in above diagrams
document.write("Articulation points in first graph <br>");
let g1 = new Graph(5);
g1.addEdge(1, 0);
g1.addEdge(0, 2);
g1.addEdge(2, 1);
g1.addEdge(0, 3);
g1.addEdge(3, 4);
g1.AP();
document.write("<br>");
document.write("Articulation points in Second graph <br>");
let g2 = new Graph(4);
g2.addEdge(0, 1);
g2.addEdge(1, 2);
g2.addEdge(2, 3);
g2.AP();
document.write("<br>");
document.write("Articulation points in Third graph <br>");
let g3 = new Graph(7);
g3.addEdge(0, 1);
g3.addEdge(1, 2);
g3.addEdge(2, 0);
g3.addEdge(1, 3);
g3.addEdge(1, 4);
g3.addEdge(1, 6);
g3.addEdge(3, 5);
g3.addEdge(4, 5);
g3.AP();
// This code is contributed by avanitrachhadiya2155
</script>
OutputArticulation points in first graph
0 3
Articulation points in second graph
1 2
Articulation points in third graph
1
Time Complexity: O(V+E), For DFS it takes O(V+E) time.
Auxiliary Space: O(V+E), For visited array, adjacency list array.
Share your thoughts in the comments
Please Login to comment...