Tarjan’s Algorithm to find Strongly Connected Components

A directed graph is strongly connected if there is a path between all pairs of vertices. A strongly connected component (SCC) of a directed graph is a maximal strongly connected subgraph. For example, there are 3 SCCs in the following graph:

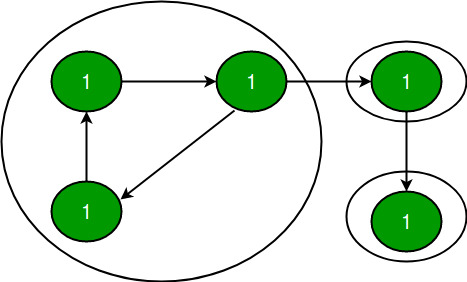
We have discussed Kosaraju’s algorithm for strongly connected components. The previously discussed algorithm requires two DFS traversals of a Graph. In this post, Tarjan’s algorithm is discussed that requires only one DFS traversal:

Tarjan Algorithm is based on the following facts: 

• DFS search produces a DFS tree/forest 
• Strongly Connected Components form subtrees of the DFS tree. 
• If we can find the head of such subtrees, we can print/store all the nodes in that subtree (including the head) and that will be one SCC. 
• There is no back edge from one SCC to another (There can be cross edges, but cross edges will not be used while processing the graph).

To find the head of an SCC, we calculate the disc and low array (as done for articulation point, bridge, and biconnected component). As discussed in the previous posts, low[u] indicates the earliest visited vertex (the vertex with minimum discovery time) that can be reached from a subtree rooted with u. A node u is head if disc[u] = low[u]

Below is an illustration of the above approach:  

To solve the problem follow the below idea:

Strongly Connected Component relates to directed graph only, but Disc and Low values relate to both directed and undirected graph, so in the above pic we have taken an undirected graph.

In the above Figure, we have shown a graph and one of the DFS trees (There could be different DFS trees on the same graph depending on the order in which edges are traversed). In a DFS tree, continuous arrows are tree edges, and dashed arrows are back edges (DFS Tree Edges ). Disc and Low values are shown in the Figure for every node as (Disc/Low). 

Disc: This is the time when a node is visited 1^st time while DFS traversal. For nodes A, B, C, .., and J in the DFS tree, Disc values are 1, 2, 3, .., 10. 

Low: In the DFS tree, Tree edges take us forward, from the ancestor node to one of its descendants. For example, from node C, tree edges can take us to node G, node I, etc. Back edges take us backward, from a descendant node to one of its ancestors. 

For example: From node G, the Back edges take us to E or C. If we look at both the Tree and Back edges together, then we can see that if we start traversal from one node, we may go down the tree via Tree edges and then go up via back edges. 

For example, from node E, we can go down to G and then go up to C. Similarly from E, we can go down to I or J and then go up to F. “Low” value of a node tells the topmost reachable ancestor (with minimum possible Disc value) via the subtree of that node. So for any node, a Low value is equal to its Disc value anyway (A node is the ancestor of itself). Then we look into its subtree and see if there is any node that can take us to any of its ancestors. 

If there are multiple back edges in the subtree that take us to different ancestors, then we take the one with the minimum Disc value (i.e. the topmost one). If we look at node F, it has two subtrees. Subtree with node G takes us to E and C. The other subtree takes us back to F only. Here topmost ancestor is C where F can reach and so the Low value of F is 3 (The Disc value of C). 

Based on the above discussion, it should be clear that the Low values of B, C, and D are 1 (As A is the topmost node where B, C, and D can reach). In the same way, the Low values of E, F, and G are 3, and the Low values of H, I, and J are 6.
For any node u, when DFS starts, Low will be set to its Disc 1^st

Then later on DFS will be performed on each of its children v one by one, Low value of u can change in two cases: 

• Case1 (Tree Edge): If node v is not visited already, then after the DFS of v is complete, a minimum of low[u] and low[v] will be updated to low[u]. 
  low[u] = min(low[u], low[v]); 
• Case 2 (Back Edge): When child v is already visited, then a minimum of low[u] and Disc[v] will be updated to low[u]. 
  low[u] = min(low[u], disc[v]); 

In case two, can we take low[v] instead of the disc[v] ?? The answer is NO. If you can think why the answer is NO, you probably understood the Low and Disc concept.

Same Low and Disc values help to solve other graph problems like articulation point, bridge, and biconnected component. To track the subtree rooted at the head, we can use a stack (keep pushing the node while visiting). When a head node is found, pop all nodes from the stack till you get the head out of the stack. To make sure, we don’t consider cross edges, when we reach a node that is already visited, we should process the visited node only if it is present in the stack, or else ignore the node.  

Below is the implementation of Tarjan’s algorithm to print all SCCs. 

C++

// A C++ program to find strongly connected components in a
// given directed graph using Tarjan's algorithm (single
// DFS)
#include <bits/stdc++.h>
#define NIL -1
using namespace std;

// A class that represents an directed graph
class Graph {
    int V; // No. of vertices
    list<int>* adj; // A dynamic array of adjacency lists

    // A Recursive DFS based function used by SCC()
    void SCCUtil(int u, int disc[], int low[],
                 stack<int>* st, bool stackMember[]);

public:
    Graph(int V); // Constructor
    void addEdge(int v,
                 int w); // function to add an edge to graph
    void SCC(); // prints strongly connected components
};

Graph::Graph(int V)
{
    this->V = V;
    adj = new list<int>[V];
}

void Graph::addEdge(int v, int w) { adj[v].push_back(w); }

// A recursive function that finds and prints strongly
// connected components using DFS traversal u --> The vertex
// to be visited next disc[] --> Stores discovery times of
// visited vertices low[] -- >> earliest visited vertex (the
// vertex with minimum
//             discovery time) that can be reached from
//             subtree rooted with current vertex
// *st -- >> To store all the connected ancestors (could be
// part
//         of SCC)
// stackMember[] --> bit/index array for faster check
// whether
//                 a node is in stack
void Graph::SCCUtil(int u, int disc[], int low[],
                    stack<int>* st, bool stackMember[])
{
    // A static variable is used for simplicity, we can
    // avoid use of static variable by passing a pointer.
    static int time = 0;

    // Initialize discovery time and low value
    disc[u] = low[u] = ++time;
    st->push(u);
    stackMember[u] = true;

    // Go through all vertices adjacent to this
    list<int>::iterator i;
    for (i = adj[u].begin(); i != adj[u].end(); ++i) {
        int v = *i; // v is current adjacent of 'u'

        // If v is not visited yet, then recur for it
        if (disc[v] == -1) {
            SCCUtil(v, disc, low, st, stackMember);

            // Check if the subtree rooted with 'v' has a
            // connection to one of the ancestors of 'u'
            // Case 1 (per above discussion on Disc and Low
            // value)
            low[u] = min(low[u], low[v]);
        }

        // Update low value of 'u' only of 'v' is still in
        // stack (i.e. it's a back edge, not cross edge).
        // Case 2 (per above discussion on Disc and Low
        // value)
        else if (stackMember[v] == true)
            low[u] = min(low[u], disc[v]);
    }

    // head node found, pop the stack and print an SCC
    int w = 0; // To store stack extracted vertices
    if (low[u] == disc[u]) {
        while (st->top() != u) {
            w = (int)st->top();
            cout << w << " ";
            stackMember[w] = false;
            st->pop();
        }
        w = (int)st->top();
        cout << w << "\n";
        stackMember[w] = false;
        st->pop();
    }
}

// The function to do DFS traversal. It uses SCCUtil()
void Graph::SCC()
{
    int* disc = new int[V];
    int* low = new int[V];
    bool* stackMember = new bool[V];
    stack<int>* st = new stack<int>();

    // Initialize disc and low, and stackMember arrays
    for (int i = 0; i < V; i++) {
        disc[i] = NIL;
        low[i] = NIL;
        stackMember[i] = false;
    }

    // Call the recursive helper function to find strongly
    // connected components in DFS tree with vertex 'i'
    for (int i = 0; i < V; i++)
        if (disc[i] == NIL)
            SCCUtil(i, disc, low, st, stackMember);
}

// Driver program to test above function
int main()
{
    cout << "\nSCCs in first graph \n";
    Graph g1(5);
    g1.addEdge(1, 0);
    g1.addEdge(0, 2);
    g1.addEdge(2, 1);
    g1.addEdge(0, 3);
    g1.addEdge(3, 4);
    g1.SCC();

    cout << "\nSCCs in second graph \n";
    Graph g2(4);
    g2.addEdge(0, 1);
    g2.addEdge(1, 2);
    g2.addEdge(2, 3);
    g2.SCC();

    cout << "\nSCCs in third graph \n";
    Graph g3(7);
    g3.addEdge(0, 1);
    g3.addEdge(1, 2);
    g3.addEdge(2, 0);
    g3.addEdge(1, 3);
    g3.addEdge(1, 4);
    g3.addEdge(1, 6);
    g3.addEdge(3, 5);
    g3.addEdge(4, 5);
    g3.SCC();

    cout << "\nSCCs in fourth graph \n";
    Graph g4(11);
    g4.addEdge(0, 1);
    g4.addEdge(0, 3);
    g4.addEdge(1, 2);
    g4.addEdge(1, 4);
    g4.addEdge(2, 0);
    g4.addEdge(2, 6);
    g4.addEdge(3, 2);
    g4.addEdge(4, 5);
    g4.addEdge(4, 6);
    g4.addEdge(5, 6);
    g4.addEdge(5, 7);
    g4.addEdge(5, 8);
    g4.addEdge(5, 9);
    g4.addEdge(6, 4);
    g4.addEdge(7, 9);
    g4.addEdge(8, 9);
    g4.addEdge(9, 8);
    g4.SCC();

    cout << "\nSCCs in fifth graph \n";
    Graph g5(5);
    g5.addEdge(0, 1);
    g5.addEdge(1, 2);
    g5.addEdge(2, 3);
    g5.addEdge(2, 4);
    g5.addEdge(3, 0);
    g5.addEdge(4, 2);
    g5.SCC();

    return 0;
}

Java

// Java program to find strongly connected
// components in a given directed graph
// using Tarjan's algorithm (single DFS)
import java.io.*;
import java.util.*;

// This class represents a directed graph
// using adjacency list representation
class Graph {

    // No. of vertices
    private int V;

    // Adjacency Lists
    private LinkedList<Integer> adj[];
    private int Time;

    // Constructor
    @SuppressWarnings("unchecked") Graph(int v)
    {
        V = v;
        adj = new LinkedList[v];

        for (int i = 0; i < v; ++i)
            adj[i] = new LinkedList();

        Time = 0;
    }

    // Function to add an edge into the graph
    void addEdge(int v, int w) { adj[v].add(w); }

    // A recursive function that finds and prints strongly
    // connected components using DFS traversal
    // u --> The vertex to be visited next
    // disc[] --> Stores discovery times of visited vertices
    // low[] -- >> earliest visited vertex (the vertex with
    //             minimum discovery time) that can be
    //             reached from subtree rooted with current
    //             vertex
    // st -- >> To store all the connected ancestors (could
    // be part
    //         of SCC)
    // stackMember[] --> bit/index array for faster check
    //                   whether a node is in stack
    void SCCUtil(int u, int low[], int disc[],
                 boolean stackMember[], Stack<Integer> st)
    {

        // Initialize discovery time and low value
        disc[u] = Time;
        low[u] = Time;
        Time += 1;
        stackMember[u] = true;
        st.push(u);

        int n;

        // Go through all vertices adjacent to this
        Iterator<Integer> i = adj[u].iterator();

        while (i.hasNext()) {
            n = i.next();

            if (disc[n] == -1) {
                SCCUtil(n, low, disc, stackMember, st);

                // Check if the subtree rooted with v
                // has a connection to one of the
                // ancestors of u
                // Case 1 (per above discussion on
                // Disc and Low value)
                low[u] = Math.min(low[u], low[n]);
            }
            else if (stackMember[n] == true) {

                // Update low value of 'u' only if 'v' is
                // still in stack (i.e. it's a back edge,
                // not cross edge).
                // Case 2 (per above discussion on Disc
                // and Low value)
                low[u] = Math.min(low[u], disc[n]);
            }
        }

        // head node found, pop the stack and print an SCC
        // To store stack extracted vertices
        int w = -1;
        if (low[u] == disc[u]) {
            while (w != u) {
                w = (int)st.pop();
                System.out.print(w + " ");
                stackMember[w] = false;
            }
            System.out.println();
        }
    }

    // The function to do DFS traversal.
    // It uses SCCUtil()
    void SCC()
    {

        // Mark all the vertices as not visited
        // and Initialize parent and visited,
        // and ap(articulation point) arrays
        int disc[] = new int[V];
        int low[] = new int[V];
        for (int i = 0; i < V; i++) {
            disc[i] = -1;
            low[i] = -1;
        }

        boolean stackMember[] = new boolean[V];
        Stack<Integer> st = new Stack<Integer>();

        // Call the recursive helper function
        // to find articulation points
        // in DFS tree rooted with vertex 'i'
        for (int i = 0; i < V; i++) {
            if (disc[i] == -1)
                SCCUtil(i, low, disc, stackMember, st);
        }
    }

    // Driver code
    public static void main(String args[])
    {

        // Create a graph given in the above diagram
        Graph g1 = new Graph(5);

        g1.addEdge(1, 0);
        g1.addEdge(0, 2);
        g1.addEdge(2, 1);
        g1.addEdge(0, 3);
        g1.addEdge(3, 4);
        System.out.println("SSC in first graph ");
        g1.SCC();

        Graph g2 = new Graph(4);
        g2.addEdge(0, 1);
        g2.addEdge(1, 2);
        g2.addEdge(2, 3);
        System.out.println("\nSSC in second graph ");
        g2.SCC();

        Graph g3 = new Graph(7);
        g3.addEdge(0, 1);
        g3.addEdge(1, 2);
        g3.addEdge(2, 0);
        g3.addEdge(1, 3);
        g3.addEdge(1, 4);
        g3.addEdge(1, 6);
        g3.addEdge(3, 5);
        g3.addEdge(4, 5);
        System.out.println("\nSSC in third graph ");
        g3.SCC();

        Graph g4 = new Graph(11);
        g4.addEdge(0, 1);
        g4.addEdge(0, 3);
        g4.addEdge(1, 2);
        g4.addEdge(1, 4);
        g4.addEdge(2, 0);
        g4.addEdge(2, 6);
        g4.addEdge(3, 2);
        g4.addEdge(4, 5);
        g4.addEdge(4, 6);
        g4.addEdge(5, 6);
        g4.addEdge(5, 7);
        g4.addEdge(5, 8);
        g4.addEdge(5, 9);
        g4.addEdge(6, 4);
        g4.addEdge(7, 9);
        g4.addEdge(8, 9);
        g4.addEdge(9, 8);
        System.out.println("\nSSC in fourth graph ");
        g4.SCC();

        Graph g5 = new Graph(5);
        g5.addEdge(0, 1);
        g5.addEdge(1, 2);
        g5.addEdge(2, 3);
        g5.addEdge(2, 4);
        g5.addEdge(3, 0);
        g5.addEdge(4, 2);
        System.out.println("\nSSC in fifth graph ");
        g5.SCC();
    }
}

// This code is contributed by
// Prateek Gupta (@prateekgupta10)

Python3

# Python program to find strongly connected components in a given
# directed graph using Tarjan's algorithm (single DFS)
#Complexity : O(V+E)

from collections import defaultdict

# This class represents an directed graph
# using adjacency list representation


class Graph:

    def __init__(self, vertices):
        # No. of vertices
        self.V = vertices

        # default dictionary to store graph
        self.graph = defaultdict(list)

        self.Time = 0

    # function to add an edge to graph
    def addEdge(self, u, v):
        self.graph[u].append(v)

    '''A recursive function that find finds and prints strongly connected
    components using DFS traversal
    u --> The vertex to be visited next
    disc[] --> Stores discovery times of visited vertices
    low[] -- >> earliest visited vertex (the vertex with minimum
                discovery time) that can be reached from subtree
                rooted with current vertex
     st -- >> To store all the connected ancestors (could be part
           of SCC)
     stackMember[] --> bit/index array for faster check whether
                  a node is in stack
    '''

    def SCCUtil(self, u, low, disc, stackMember, st):

        # Initialize discovery time and low value
        disc[u] = self.Time
        low[u] = self.Time
        self.Time += 1
        stackMember[u] = True
        st.append(u)

        # Go through all vertices adjacent to this
        for v in self.graph[u]:

            # If v is not visited yet, then recur for it
            if disc[v] == -1:

                self.SCCUtil(v, low, disc, stackMember, st)

                # Check if the subtree rooted with v has a connection to
                # one of the ancestors of u
                # Case 1 (per above discussion on Disc and Low value)
                low[u] = min(low[u], low[v])

            elif stackMember[v] == True:

                '''Update low value of 'u' only if 'v' is still in stack
                (i.e. it's a back edge, not cross edge).
                Case 2 (per above discussion on Disc and Low value) '''
                low[u] = min(low[u], disc[v])

        # head node found, pop the stack and print an SCC
        w = -1  # To store stack extracted vertices
        if low[u] == disc[u]:
            while w != u:
                w = st.pop()
                print(w, end=" ")
                stackMember[w] = False

            print()

    # The function to do DFS traversal.
    # It uses recursive SCCUtil()

    def SCC(self):

        # Mark all the vertices as not visited
        # and Initialize parent and visited,
        # and ap(articulation point) arrays
        disc = [-1] * (self.V)
        low = [-1] * (self.V)
        stackMember = [False] * (self.V)
        st = []

        # Call the recursive helper function
        # to find articulation points
        # in DFS tree rooted with vertex 'i'
        for i in range(self.V):
            if disc[i] == -1:
                self.SCCUtil(i, low, disc, stackMember, st)


# Create a graph given in the above diagram
g1 = Graph(5)
g1.addEdge(1, 0)
g1.addEdge(0, 2)
g1.addEdge(2, 1)
g1.addEdge(0, 3)
g1.addEdge(3, 4)
print("SSC in first graph ")
g1.SCC()

g2 = Graph(4)
g2.addEdge(0, 1)
g2.addEdge(1, 2)
g2.addEdge(2, 3)
print("\nSSC in second graph ")
g2.SCC()


g3 = Graph(7)
g3.addEdge(0, 1)
g3.addEdge(1, 2)
g3.addEdge(2, 0)
g3.addEdge(1, 3)
g3.addEdge(1, 4)
g3.addEdge(1, 6)
g3.addEdge(3, 5)
g3.addEdge(4, 5)
print("\nSSC in third graph ")
g3.SCC()

g4 = Graph(11)
g4.addEdge(0, 1)
g4.addEdge(0, 3)
g4.addEdge(1, 2)
g4.addEdge(1, 4)
g4.addEdge(2, 0)
g4.addEdge(2, 6)
g4.addEdge(3, 2)
g4.addEdge(4, 5)
g4.addEdge(4, 6)
g4.addEdge(5, 6)
g4.addEdge(5, 7)
g4.addEdge(5, 8)
g4.addEdge(5, 9)
g4.addEdge(6, 4)
g4.addEdge(7, 9)
g4.addEdge(8, 9)
g4.addEdge(9, 8)
print("\nSSC in fourth graph ")
g4.SCC()


g5 = Graph(5)
g5.addEdge(0, 1)
g5.addEdge(1, 2)
g5.addEdge(2, 3)
g5.addEdge(2, 4)
g5.addEdge(3, 0)
g5.addEdge(4, 2)
print("\nSSC in fifth graph ")
g5.SCC()

# This code is contributed by Neelam Yadav

Javascript

<script>

// Javascript program to find strongly connected
// components in a given directed graph
// using Tarjan's algorithm (single DFS)

// This class represents a directed graph
// using adjacency list representation
class Graph{

// Constructor
constructor(v)
{
    this.V = v;
    this.adj = new Array(v);

    for(let i = 0; i < v; ++i)
        this.adj[i] = [];

    this.Time = 0;
}

// Function to add an edge into the graph
addEdge(v, w)
{
    this.adj[v].push(w);
}

// A recursive function that finds and prints strongly
// connected components using DFS traversal
// u --> The vertex to be visited next
// disc[] --> Stores discovery times of visited vertices
// low[] -- >> earliest visited vertex (the vertex with
//             minimum discovery time) that can be reached
//             from subtree rooted with current vertex
// st -- >> To store all the connected ancestors (could be
//          part of SCC)
// stackMember[] --> bit/index array for faster check
//                   whether a node is in stack
SCCUtil(u, low, disc, stackMember, st)
{

    // Initialize discovery time and low value
    disc[u] = this.Time;
    low[u] = this.Time;
    this.Time += 1;
    stackMember[u] = true;
    st.push(u);

    let n;

    // Go through all vertices adjacent to this
    for(let i of this.adj[u])
    {
        n = i;

        if (disc[n] == -1)
        {
            this.SCCUtil(n, low, disc, stackMember, st);

            // Check if the subtree rooted with v
            // has a connection to one of the
            // ancestors of u
            // Case 1 (per above discussion on
            // Disc and Low value)
            low[u] = Math.min(low[u], low[n]);
        }
        else if (stackMember[n] == true)
        {

            // Update low value of 'u' only if 'v' is
            // still in stack (i.e. it's a back edge,
            // not cross edge).
            // Case 2 (per above discussion on Disc
            // and Low value)
            low[u] = Math.min(low[u], disc[n]);
        }
    }

    // Head node found, pop the stack and print an SCC
    // To store stack extracted vertices
    let w = -1;
    if (low[u] == disc[u])
    {
        while (w != u)
        {
            w = st.pop();
            document.write(w + " ");
            stackMember[w] = false;
        }
        document.write("<br>");
    }
    }

// The function to do DFS traversal.
// It uses SCCUtil()
SCC()
{

    // Mark all the vertices as not visited
    // and Initialize parent and visited,
    // and ap(articulation point) arrays
    let disc = new Array(this.V);
    let low = new Array(this.V);
    for(let i = 0;i < this.V; i++)
    {
        disc[i] = -1;
        low[i] = -1;
    }

    let stackMember = new Array(this.V);
    let st = [];

    // Call the recursive helper function
    // to find articulation points
    // in DFS tree rooted with vertex 'i'
    for(let i = 0; i < this.V; i++)
    {
        if (disc[i] == -1)
            this.SCCUtil(i, low, disc,
                         stackMember, st);
    }
}
}

// Driver code

// Create a graph given in the above diagram
let g1 = new Graph(5);

g1.addEdge(1, 0);
g1.addEdge(0, 2);
g1.addEdge(2, 1);
g1.addEdge(0, 3);
g1.addEdge(3, 4);
document.write("SSC in first graph <br>");
g1.SCC();

let g2 = new Graph(4);
g2.addEdge(0, 1);
g2.addEdge(1, 2);
g2.addEdge(2, 3);
document.write("\nSSC in second graph<br> ");
g2.SCC();

let g3 = new Graph(7);
g3.addEdge(0, 1);
g3.addEdge(1, 2);
g3.addEdge(2, 0);
g3.addEdge(1, 3);
g3.addEdge(1, 4);
g3.addEdge(1, 6);
g3.addEdge(3, 5);
g3.addEdge(4, 5);
document.write("\nSSC in third graph <br>");
g3.SCC();

let g4 = new Graph(11);
g4.addEdge(0, 1);
g4.addEdge(0, 3);
g4.addEdge(1, 2);
g4.addEdge(1, 4);
g4.addEdge(2, 0);
g4.addEdge(2, 6);
g4.addEdge(3, 2);
g4.addEdge(4, 5);
g4.addEdge(4, 6);
g4.addEdge(5, 6);
g4.addEdge(5, 7);
g4.addEdge(5, 8);
g4.addEdge(5, 9);
g4.addEdge(6, 4);
g4.addEdge(7, 9);
g4.addEdge(8, 9);
g4.addEdge(9, 8);
document.write("\nSSC in fourth graph<br> ");
g4.SCC();

let g5 = new Graph (5);
g5.addEdge(0, 1);
g5.addEdge(1, 2);
g5.addEdge(2, 3);
g5.addEdge(2, 4);
g5.addEdge(3, 0);
g5.addEdge(4, 2);
document.write("\nSSC in fifth graph <br>");
g5.SCC();

// This code is contributed by avanitrachhadiya2155

</script>

C#

using System;
using System.Collections.Generic;

// This class represents a directed graph
// using adjacency list representation
class Graph
{
    // No. of vertices
    private int V;

    // Adjacency Lists
    private List<int>[] adj;
    private int Time;

    // Constructor
    public Graph(int v)
    {
        V = v;
        adj = new List<int>[v];

        for (int i = 0; i < v; ++i)
            adj[i] = new List<int>();

        Time = 0;
    }

    // Function to add an edge into the graph
    public void addEdge(int v, int w) { adj[v].Add(w); }

    // A recursive function that finds and prints strongly
    // connected components using DFS traversal
    // u --> The vertex to be visited next
    // disc[] --> Stores discovery times of visited vertices
    // low[] -- >> earliest visited vertex (the vertex with
    //             minimum discovery time) that can be
    //             reached from subtree rooted with current
    //             vertex
    // st -- >> To store all the connected ancestors (could
    // be part
    //         of SCC)
    // stackMember[] --> bit/index array for faster check
    //                   whether a node is in stack
    private void SCCUtil(int u, int[] low, int[] disc,
                 bool[] stackMember, Stack<int> st)
    {

        // Initialize discovery time and low value
        disc[u] = Time;
        low[u] = Time;
        Time += 1;
        stackMember[u] = true;
        st.Push(u);

        int n;

        // Go through all vertices adjacent to this
        foreach (int i in adj[u])
        {
            n = i;

            if (disc[n] == -1)
            {
                SCCUtil(n, low, disc, stackMember, st);

                // Check if the subtree rooted with v
                // has a connection to one of the
                // ancestors of u
                // Case 1 (per above discussion on
                // Disc and Low value)
                low[u] = Math.Min(low[u], low[n]);
            }
            else if (stackMember[n] == true)
            {
                // Update low value of 'u' only if 'v' is
                // still in stack (i.e. it's a back edge,
                // not cross edge).
                // Case 2 (per above discussion on Disc
                // and Low value)
                low[u] = Math.Min(low[u], disc[n]);
            }
        }

        // head node found, pop the stack and print an SCC
        // To store stack extracted vertices
        int w = -1;
        if (low[u] == disc[u])
        {
            while (w != u)
            {
                w = st.Pop();
                Console.Write(w + " ");
                stackMember[w] = false;
            }
            Console.WriteLine();
        }
    }

    // The function to do DFS traversal.
    // It uses SCCUtil()
    public void SCC()
    {
        // Mark all the vertices as not visited
        // and Initialize parent and visited,
        // and ap(articulation point) arrays
        int[] disc = new int[V];
        int[] low = new int[V];
        for (int i = 0; i < V; i++)
        {
            disc[i] = -1;
            low[i] = -1;
        }

        bool[] stackMember = new bool[V];
        Stack<int> st = new Stack<int>();
            // Call the recursive helper function
    // to find strongly connected components
    for (int i = 0; i < V; i++)
        if (disc[i] == -1)
            SCCUtil(i, low, disc, stackMember, st);
}
static void Main(string[] args)
{
    // Create a new graph with 5 vertices
    Graph g = new Graph(5);

    // Add edges to the graph
    g.addEdge(1, 0);
    g.addEdge(0, 2);
    g.addEdge(2, 1);
    g.addEdge(0, 3);
    g.addEdge(3, 4);

    Console.WriteLine("Strongly Connected Components:");
    g.SCC();

        Graph g2 = new Graph(4);
        g2.addEdge(0, 1);
        g2.addEdge(1, 2);
        g2.addEdge(2, 3);
        Console.WriteLine("\nSSC in second graph ");
        g2.SCC();

        Graph g3 = new Graph(7);
        g3.addEdge(0, 1);
        g3.addEdge(1, 2);
        g3.addEdge(2, 0);
        g3.addEdge(1, 3);
        g3.addEdge(1, 4);
        g3.addEdge(1, 6);
        g3.addEdge(3, 5);
        g3.addEdge(4, 5);
      Console.WriteLine("\nSSC in third graph ");
        g3.SCC();

        Graph g4 = new Graph(11);
        g4.addEdge(0, 1);
        g4.addEdge(0, 3);
        g4.addEdge(1, 2);
        g4.addEdge(1, 4);
        g4.addEdge(2, 0);
        g4.addEdge(2, 6);
        g4.addEdge(3, 2);
        g4.addEdge(4, 5);
        g4.addEdge(4, 6);
        g4.addEdge(5, 6);
        g4.addEdge(5, 7);
        g4.addEdge(5, 8);
        g4.addEdge(5, 9);
        g4.addEdge(6, 4);
        g4.addEdge(7, 9);
        g4.addEdge(8, 9);
        g4.addEdge(9, 8);
        Console.WriteLine("\nSSC in fourth graph ");
        g4.SCC();

        Graph g5 = new Graph(5);
        g5.addEdge(0, 1);
        g5.addEdge(1, 2);
        g5.addEdge(2, 3);
        g5.addEdge(2, 4);
        g5.addEdge(3, 0);
        g5.addEdge(4, 2);
        Console.WriteLine("\nSSC in fifth graph ");
        g5.SCC();
}
}

Output

SCCs in first graph 
4
3
1 2 0

SCCs in second graph 
3
2
1
0

SCCs in third graph 
5
3
4
6
2 1 0

SCCs in fourth graph 
8 9
7
5 4 6
3 2 1 0
10

SCCs in fifth graph 
4 3 2 1 0

Time Complexity: The above algorithm mainly calls DFS, DFS takes O(V+E) for a graph represented using an adjacency list. 
Auxiliary Space: O(V)