BFS for Disconnected Graph

In the previous post, BFS only with a particular vertex is performed i.e. it is assumed that all vertices are reachable from the starting vertex. But in the case of a disconnected graph or any vertex that is unreachable from all vertex, the previous implementation will not give the desired output, so in this post, a modification is done in BFS. 

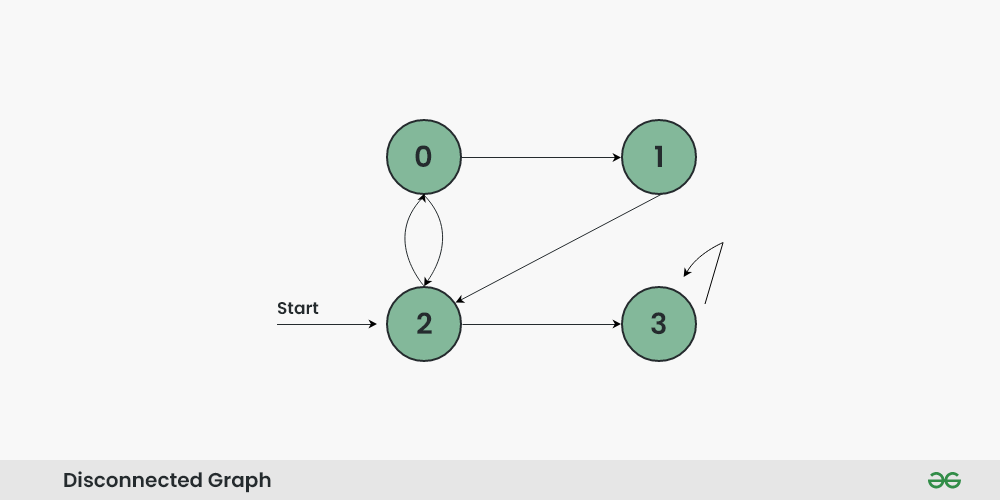
 All vertices are reachable. So, for the above graph, simple BFS will work. 

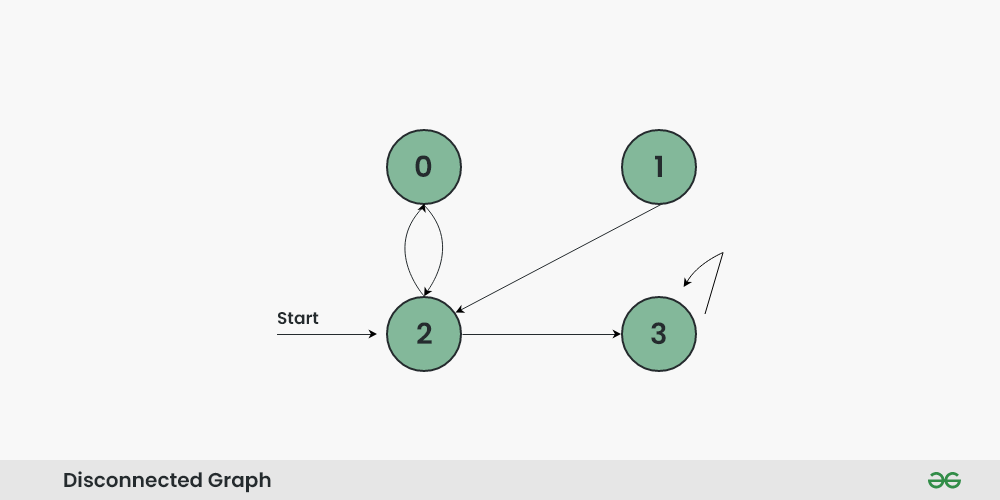
 As in the above graph vertex 1 is unreachable from all vertex, so simple BFS wouldn’t work for it.

Just to modify BFS, perform simple BFS from each 
unvisited vertex of given graph.

Following is the code when adjacency matrix representation is used for the graph.

C++

// C++ implementation of modified BFS for adjacency matrix
// representation
#include <iostream>
#include <queue>
using namespace std;
void printBFS(int** edges, int V, int start, int* visited);
void BFSHelper(int** edges, int V);
void addEdge(int** edges, int f, int s);

void addEdge(int** edges, int f, int s) { edges[f][s] = 1; }
void printBFS(int** edges, int V, int start, int* visited)
{
    if (V == 0)
        return;
    queue<int> BFS;
    BFS.push(start);
    visited[start] = 1;
    while (!BFS.empty()) {
        int data = BFS.front();
        BFS.pop();
        cout << data << " ";
        for (int i = 0; i < V; i++) {
            if (edges[data][i] == 1) {
                if (visited[i] == 0) {
                    BFS.push(i);
                    visited[i] = 1;
                }
            }
        }
    }
}

void BFSHelper(int** edges, int V)
{
    if (V == 0)
        return;
    int* visited = new int[V];
    for (int i = 0; i < V; i++) {
        visited[i] = 0;
    }
    for (int i = 0; i < V; i++) {
        if (visited[i] == 0) {
            printBFS(edges, V, i, visited);
        }
    }
}

int main()
{
    int V = 5;
    int E = 6;
    if (E == 0) {
        for (int i = 0; i < V; i++) {
            cout << i << " ";
        }
        return 0;
    }
    int** edges = new int*[V];
    for (int i = 0; i < V; i++) {
        edges[i] = new int[V];
        for (int j = 0; j < V; j++) {
            edges[i][j] = 0;
        }
    }

    addEdge(edges, 0, 4);
    addEdge(edges, 1, 2);
    addEdge(edges, 1, 3);
    addEdge(edges, 1, 4);
    addEdge(edges, 2, 3);
    addEdge(edges, 3, 4);

    BFSHelper(edges, V);
    return 0;
}

Java

// Java implementation of modified BFS for adjacency matrix
// representation

import java.io.*;
import java.util.*;

class GFG {
  static void addEdge(int[][] edges, int f, int s)
  {
    edges[f][s] = 1;
  }

  static void printBFS(int[][] edges, int V, int start,
                       int[] visited)
  {
    if (V == 0)
      return;
    Queue<Integer> BFS = new LinkedList<Integer>();
    BFS.add(start);
    visited[start] = 1;
    while (!BFS.isEmpty()) {
      int data = BFS.poll();
      System.out.print(data + " ");
      for (int i = 0; i < V; i++) {
        if (edges[data][i] == 1) {
          if (visited[i] == 0) {
            BFS.add(i);
            visited[i] = 1;
          }
        }
      }
    }
  }

  static void bfsHelper(int[][] edges, int V)
  {
    if (V == 0)
      return;
    int[] visited = new int[V];
    for (int i = 0; i < V; i++) {
      visited[i] = 0;
    }
    for (int i = 0; i < V; i++) {
      if (visited[i] == 0) {
        printBFS(edges, V, i, visited);
      }
    }
    System.out.println();
  }

  public static void main(String[] args)
  {
    int V = 5;
    int E = 6;
    if (E == 0) {
      for (int i = 0; i < V; i++) {
        System.out.print(i + " ");
      }
      System.out.println();
      System.exit(0);
    }
    int[][] edges = new int[V][V];
    for (int i = 0; i < V; i++) {
      for (int j = 0; j < V; j++) {
        edges[i][j] = 0;
      }
    }

    addEdge(edges, 0, 4);
    addEdge(edges, 1, 2);
    addEdge(edges, 1, 3);
    addEdge(edges, 1, 4);
    addEdge(edges, 2, 3);
    addEdge(edges, 3, 4);

    bfsHelper(edges, V);
  }
}

// This code is contributed by cavi4762.

Python3

import queue

def add_edge(edges, f, s):
    edges[f][s] = 1

def print_bfs(edges, V, start, visited):
    if V == 0:
        return
    bfs = queue.Queue()
    bfs.put(start)
    visited[start] = 1
    while not bfs.empty():
        data = bfs.get()
        print(data, end=' ')
        for i in range(V):
            if edges[data][i] == 1:
                if visited[i] == 0:
                    bfs.put(i)
                    visited[i] = 1

def bfs_helper(edges, V):
    if V == 0:
        return
    visited = [0] * V
    for i in range(V):
        if visited[i] == 0:
            print_bfs(edges, V, i, visited)

if __name__ == "__main__":
    V = 5
    E = 6
    if E == 0:
        for i in range(V):
            print(i, end=' ')
        exit()

    edges = [[0 for _ in range(V)] for _ in range(V)]

    add_edge(edges, 0, 4)
    add_edge(edges, 1, 2)
    add_edge(edges, 1, 3)
    add_edge(edges, 1, 4)
    add_edge(edges, 2, 3)
    add_edge(edges, 3, 4)

    bfs_helper(edges, V)

C#

// C# implementation of modified BFS for adjacency matrix
// representation

using System;
using System.Collections.Generic;

class Gfg {
  static void AddEdge(int[, ] edges, int f, int s)
  {
    edges[f, s] = 1;
  }

  static void PrintBFS(int[, ] edges, int V, int start,
                       int[] visited)
  {
    if (V == 0)
      return;
    Queue<int> BFS = new Queue<int>();
    BFS.Enqueue(start);
    visited[start] = 1;
    while (BFS.Count > 0) {
      int data = BFS.Dequeue();
      Console.Write(data + " ");
      for (int i = 0; i < V; i++) {
        if (edges[data, i] == 1) {
          if (visited[i] == 0) {
            BFS.Enqueue(i);
            visited[i] = 1;
          }
        }
      }
    }
  }

  static void BFSHelper(int[, ] edges, int V)
  {
    if (V == 0)
      return;
    int[] visited = new int[V];
    for (int i = 0; i < V; i++) {
      visited[i] = 0;
    }
    for (int i = 0; i < V; i++) {
      if (visited[i] == 0) {
        PrintBFS(edges, V, i, visited);
      }
    }
    Console.WriteLine();
  }

  static void Main(string[] args)
  {
    int V = 5;
    int E = 6;
    if (E == 0) {
      for (int i = 0; i < V; i++) {
        Console.Write(i + " ");
      }
      Console.WriteLine();
      Environment.Exit(0);
    }
    int[, ] edges = new int[V, V];
    for (int i = 0; i < V; i++) {
      for (int j = 0; j < V; j++) {
        edges[i, j] = 0;
      }
    }

    AddEdge(edges, 0, 4);
    AddEdge(edges, 1, 2);
    AddEdge(edges, 1, 3);
    AddEdge(edges, 1, 4);
    AddEdge(edges, 2, 3);
    AddEdge(edges, 3, 4);

    BFSHelper(edges, V);
  }
}

// This code is contributed by cavi4762.

Javascript

// Javascript implementation of modified BFS for adjacency matrix representation

  class Queue {
    constructor() {
      this.items = [];
    }

    // add element to the queue
    push(element) {
      return this.items.push(element);
    }

    // remove element from the queue
    pop() {
      if (this.items.length > 0) {
        return this.items.shift();
      }
    }

    // view the first element
    front() {
      return this.items[0];
    }

    // check if the queue is empty
    empty() {
      return this.items.length == 0;
    }
  }

  function addEdge(edges, f, s) {
    edges[f][s] = 1;
  }
  function printBFS(edges, V, start, visited) {
    if (V == 0) return;
    let BFS = new Queue();
    BFS.push(start);
    visited[start] = 1;
    while (!BFS.empty()) {
      data = BFS.front();
      BFS.pop();
      console.log(data);
      for (let i = 0; i < V; i++) {
        if (edges[data][i] == 1) {
          if (visited[i] == 0) {
            BFS.push(i);
            visited[i] = 1;
          }
        }
      }
    }
  }

  function BFSHelper(edges, V) {
    if (V == 0) return;
    let visited = new Array(V);
    for (let i = 0; i < V; i++) {
      visited[i] = 0;
    }
    for (let i = 0; i < V; i++) {
      if (visited[i] == 0) {
        printBFS(edges, V, i, visited);
      }
    }
  }

  let V = 5;
  let E = 6;
  if (E == 0) {
    for (let i = 0; i < V; i++) {
      console.log(i);
    }
  }

  let edges = Array.from(Array(V), () => new Array(V));
  for (let i = 0; i < V; i++) {
    for (let j = 0; j < V; j++) {
      edges[i][j] = 0;
    }
  }

  addEdge(edges, 0, 4);
  addEdge(edges, 1, 2);
  addEdge(edges, 1, 3);
  addEdge(edges, 1, 4);
  addEdge(edges, 2, 3);
  addEdge(edges, 3, 4);

  BFSHelper(edges, V);

Output

0 4 1 2 3 

The time complexity of this algorithm is O(V + E), where V is the number of vertices and E is the number of edges. This is because we traverse each vertex and each edge once. 

The space complexity is O(V), since we use an array to store the visited vertices.

Following is the code when adjacency list representation is used for the graph.

C++

// C++ implementation of modified BFS
#include<bits/stdc++.h>
using namespace std;

// A utility function to add an edge in an
// directed graph.
void addEdge(vector<int> adj[], int u, int v)
{
    adj[u].push_back(v);
}

// A utility function to do BFS of graph
// from a given vertex u.
void BFSUtil(int u, vector<int> adj[],
            vector<bool> &visited)
{

    // Create a queue for BFS
    list<int> q;

    // Mark the current node as visited and enqueue it
    visited[u] = true;
    q.push_back(u);

    // 'i' will be used to get all adjacent vertices 4
    // of a vertex list<int>::iterator i;

    while(!q.empty())
    {
        // Dequeue a vertex from queue and print it
        u = q.front();
        cout << u << " ";
        q.pop_front();

        // Get all adjacent vertices of the dequeued
        // vertex s. If an adjacent has not been visited,
        // then mark it visited and enqueue it
        for (int i = 0; i != adj[u].size(); ++i)
        {
            if (!visited[adj[u][i]])
            {
                visited[adj[u][i]] = true;
                q.push_back(adj[u][i]);
            }
        }
    }
}

// This function does BFSUtil() for all
// unvisited vertices.
void BFS(vector<int> adj[], int V)
{
    vector<bool> visited(V, false);
    for (int u=0; u<V; u++)
        if (visited[u] == false)
            BFSUtil(u, adj, visited);
}

// Driver code
int main()
{
    int V = 5;
    vector<int> adj[V];

    addEdge(adj, 0, 4);
    addEdge(adj, 1, 2);
    addEdge(adj, 1, 3);
    addEdge(adj, 1, 4);
    addEdge(adj, 2, 3);
    addEdge(adj, 3, 4);
    BFS(adj, V);
    return 0;
}

Java

// Java implementation of modified BFS
import java.util.*;
public class graph
{
    //Implementing graph using HashMap
    static HashMap<Integer,LinkedList<Integer>> graph=new HashMap<>();

    //utility function to add edge in an undirected graph
public static void addEdge(int a,int b)
{
    if(graph.containsKey(a))
    {
        LinkedList<Integer> l=graph.get(a);
        l.add(b);
        graph.put(a,l);
    }
    else
    {
        LinkedList<Integer> l=new LinkedList<>();
        l.add(b);
        graph.put(a,l);
    }
}

//Helper function for BFS
public static void bfshelp(int s,ArrayList<Boolean> visited)
{
    // Create a queue for BFS
    LinkedList<Integer> q=new LinkedList<>();

    // Mark the current node as visited and enqueue it
    q.add(s);
    visited.set(s,true);

    while(!q.isEmpty())
    {
        // Dequeue a vertex from queue and print it
        int f=q.poll();
        System.out.print(f+" ");

        //Check whether the current node is
                //connected to any other node or not
        if(graph.containsKey(f))
        {
        Iterator<Integer> i=graph.get(f).listIterator();

        // Get all adjacent vertices of the dequeued
        // vertex f. If an adjacent has not been visited,
        // then mark it visited and enqueue it

            while(i.hasNext())
            {
                int n=i.next();
                if(!visited.get(n))
                {
                visited.set(n,true);
                q.add(n);
                }
            }
        }
    }

}

//BFS function to check each node
public static void bfs(int vertex)
{
    ArrayList<Boolean> visited=new ArrayList<Boolean>();
    //Marking each node as unvisited
    for(int i=0;i<vertex;i++)
    {
        visited.add(i,false);
    }
    for(int i=0;i<vertex;i++)
    {
        //Checking whether the node is visited or not
        if(!visited.get(i))
        {
            bfshelp(i,visited);
        }
    }
}

//Driver Code-The main function
    public static void main(String[] args)
    {
        int v=5;
        addEdge(0, 4);
        addEdge(1, 2);
        addEdge(1, 3);
        addEdge(1, 4);
        addEdge(2, 3);
        addEdge(3, 4);
        bfs(v);
    }

}

Python3

# Python3 implementation of modified BFS
import queue

# A utility function to add an edge
# in an undirected graph.
def addEdge(adj, u, v):
    adj[u].append(v)

# A utility function to do BFS of
# graph from a given vertex u.
def BFSUtil(u, adj, visited):

    # Create a queue for BFS
    q = queue.Queue()

    # Mark the current node as visited
    # and enqueue it
    visited[u] = True
    q.put(u)

    # 'i' will be used to get all adjacent
    # vertices 4 of a vertex list<int>::iterator i

    while(not q.empty()):

        # Dequeue a vertex from queue
        # and print it
        u = q.queue[0]
        print(u, end = " ")
        q.get()

        # Get all adjacent vertices of the
        # dequeued vertex s. If an adjacent
        # has not been visited, then mark
        # it visited and enqueue it
        i = 0
        while i != len(adj[u]):
            if (not visited[adj[u][i]]):
                    visited[adj[u][i]] = True
                    q.put(adj[u][i])
            i += 1

# This function does BFSUtil() for all
# unvisited vertices.
def BFS(adj, V):
    visited = [False] * V
    for u in range(V):
        if (visited[u] == False):
            BFSUtil(u, adj, visited)

# Driver code
if __name__ == '__main__':

    V = 5
    adj = [[] for i in range(V)]

    addEdge(adj, 0, 4)
    addEdge(adj, 1, 2)
    addEdge(adj, 1, 3)
    addEdge(adj, 1, 4)
    addEdge(adj, 2, 3)
    addEdge(adj, 3, 4)
    BFS(adj, V)

# This code is contributed by PranchalK

C#

// C# implementation of modified BFS
using System;
using System.Collections.Generic;

class Graph
{
    //Implementing graph using Dictionary
    static Dictionary<int,List<int>> graph =
            new Dictionary<int,List<int>>();

//utility function to add edge in an undirected graph
public static void addEdge(int a, int b)
{
    if(graph.ContainsKey(a))
    {
        List<int> l = graph[a];
        l.Add(b);
        if(graph.ContainsKey(a))
            graph[a] = l;
        else
            graph.Add(a,l);
    }
    else
    {
        List<int> l = new List<int>();
        l.Add(b);
        graph.Add(a, l);
    }
}

// Helper function for BFS
public static void bfshelp(int s, List<Boolean> visited)
{
    // Create a queue for BFS
    List<int> q = new List<int>();

    // Mark the current node as visited and enqueue it
    q.Add(s);
    visited.RemoveAt(s);
    visited.Insert(s,true);

    while(q.Count != 0)
    {
        // Dequeue a vertex from queue and print it
        int f = q[0];
        q.RemoveAt(0);
        Console.Write(f + " ");

        //Check whether the current node is
        //connected to any other node or not
        if(graph.ContainsKey(f))
        {

        // Get all adjacent vertices of the dequeued
        // vertex f. If an adjacent has not been visited,
        // then mark it visited and enqueue it

            foreach(int iN in graph[f])
            {
                int n = iN;
                if(!visited[n])
                {
                    visited.RemoveAt(n);
                    visited.Insert(n, true);
                    q.Add(n);
                }
            }
        }
    }

}

// BFS function to check each node
public static void bfs(int vertex)
{
    List<Boolean> visited = new List<Boolean>();

    // Marking each node as unvisited
    for(int i = 0; i < vertex; i++)
    {
        visited.Insert(i, false);
    }
    for(int i = 0; i < vertex; i++)
    {
        // Checking whether the node is visited or not
        if(!visited[i])
        {
            bfshelp(i, visited);
        }
    }
}

// Driver Code
public static void Main(String[] args)
{
    int v = 5;
    addEdge(0, 4);
    addEdge(1, 2);
    addEdge(1, 3);
    addEdge(1, 4);
    addEdge(2, 3);
    addEdge(3, 4);
    bfs(v);
}
}

// This code is contributed by Rajput-Ji

Javascript

// JavaScript implementation of modified BFS
class Graph {
  constructor() {
    this.graph = new Map(); // Implementing graph using Map
  }

  // utility function to add edge in an undirected graph
  addEdge(a, b) {
    if (this.graph.has(a)) {
      let l = this.graph.get(a);
      l.push(b);
      this.graph.set(a, l);
    } else {
      this.graph.set(a, [b]);
    }
  }

  // Helper function for BFS
  bfshelp(s, visited) {
    // Create a queue for BFS
    let q = [];
    // Mark the current node as visited and enqueue it
    q.push(s);
    visited[s] = true;

    while (q.length > 0) {
      // Dequeue a vertex from queue and print it
      let f = q.shift();
      console.log(f + " ");

      // Check whether the current node is connected to any other node or not
      if (this.graph.has(f)) {
        let l = this.graph.get(f);
        for (let n of l) {
          // Get all adjacent vertices of the dequeued vertex f.
          // If an adjacent has not been visited, then mark it visited and enqueue it
          if (!visited[n]) {
            visited[n] = true;
            q.push(n);
          }
        }
      }
    }
  }

  // BFS function to check each node
  bfs(vertex) {
    let visited = Array(vertex).fill(false);
    // Marking each node as unvisited
    for (let i = 0; i < vertex; i++) {
      // Checking whether the node is visited or not
      if (!visited[i]) {
        this.bfshelp(i, visited);
      }
    }
  }
}

// Driver Code-The main function
let g = new Graph();
let v = 5;
g.addEdge(0, 4);
g.addEdge(1, 2);
g.addEdge(1, 3);
g.addEdge(1, 4);
g.addEdge(2, 3);
g.addEdge(3, 4);
g.bfs(v);


//This code is contributed by shivamsharma215

Output

0 4 1 2 3 

The time complexity of the given BFS algorithm is O(V + E), where V is the number of vertices and E is the number of edges in the graph. 

The space complexity is also O(V + E) since we need to store the adjacency list and the visited array.

 This article is contributed by Sahil Chhabra (akku). If you like GeeksforGeeks and would like to contribute, you can also write an article using write.geeksforgeeks.org or mail your article to review-team@geeksforgeeks.org. See your article appearing on the GeeksforGeeks main page and help other Geeks.