Fleury’s Algorithm for printing Eulerian Path or Circuit
Last Updated :
06 Jun, 2023
Eulerian Path is a path in a graph that visits every edge exactly once. Eulerian Circuit is an Eulerian Path that starts and ends on the same vertex.
We strongly recommend first reading the following post on Euler Path and Circuit. “https://www.geeksforgeeks.org/eulerian-path-and-circuit/”
In the above-mentioned post, we discussed the problem of finding out whether a given graph is Eulerian or not. In this post, an algorithm to print an Eulerian trail or circuit is discussed.
Following is Fleury’s Algorithm for printing the Eulerian trail or cycle
- Make sure the graph has either 0 or 2 odd vertices.
- If there are 0 odd vertices, start anywhere. If there are 2 odd vertices, start at one of them.
- Follow edges one at a time. If you have a choice between a bridge and a non-bridge, always choose the non-bridge.
- Stop when you run out of edges.
The idea is, “don’t burn bridges“ so that we can come back to a vertex and traverse the remaining edges. For example, let us consider the following graph.
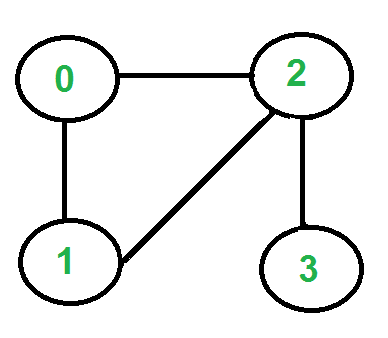
There are two vertices with odd degrees, ‘2’ and ‘3’, and we can start paths from any of them. Let us start the tour from vertex ‘2’.
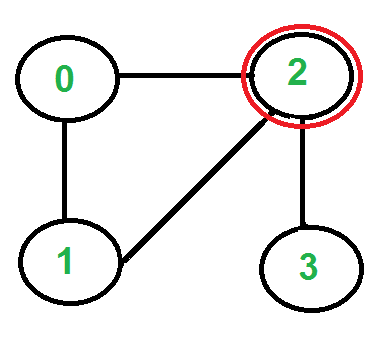
Three edges are going out from vertex ‘2’, which one to pick? We don’t pick the edge ‘2-3’ because that is a bridge (we won’t be able to come back to ‘3’). We can pick any of the remaining two edges. Let us say we pick ‘2-0’. We remove this edge and move to vertex ‘0’.
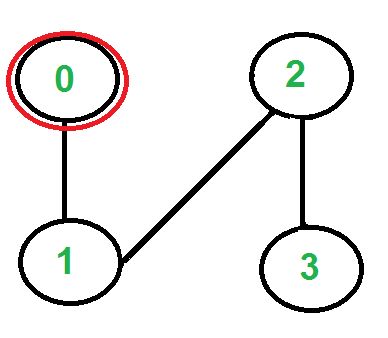
There is only one edge from vertex ‘0’, so we pick it, remove it and move to vertex ‘1’. Euler tour becomes ‘2-0 0-1’.
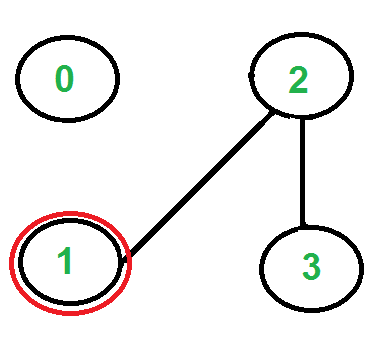
There is only one edge from vertex ‘1’, so we pick it, remove it and move to vertex ‘2’. Euler tour becomes ‘2-0 0-1 1-2’
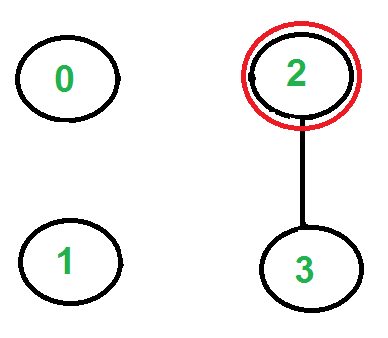
Again there is only one edge from vertex 2, so we pick it, remove it and move to vertex 3. Euler tour becomes ‘2-0 0-1 1-2 2-3’
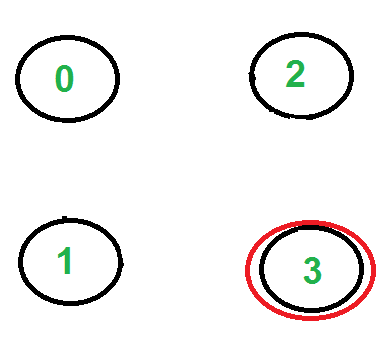
There are no more edges left, so we stop here. Final tour is ‘2-0 0-1 1-2 2-3’.
Following is the C++ implementation of the above algorithm. In the following code, it is assumed that the given graph has an Eulerian trail or Circuit. The main focus is to print an Eulerian trail or circuit. We can use isEulerian() to first check whether there is an Eulerian Trail or Circuit in the given graph.
We first find the starting point which must be an odd vertex (if there are odd vertices) and store it in variable ‘u’. If there are zero odd vertices, we start from vertex ‘0’. We call printEulerUtil() to print Euler tour starting with u. We traverse all adjacent vertices of u, if there is only one adjacent vertex, we immediately consider it. If there are more than one adjacent vertices, we consider an adjacent v only if edge u-v is not a bridge. How to find if a given edge is a bridge? We count several vertices reachable from u. We remove edge u-v and again count the number of reachable vertices from u. If the number of reachable vertices is reduced, then edge u-v is a bridge. To count reachable vertices, we can either use BFS or DFS, we have used DFS in the above code. The function DFSCount(u) returns several vertices reachable from u.
Once an edge is processed (included in the Euler tour), we remove it from the graph. To remove the edge, we replace the vertex entry with -1 in the adjacency list. Note that simply deleting the node may not work as the code is recursive and a parent call may be in the middle of the adjacency list.
C++
#include <algorithm>
#include <iostream>
#include <list>
#include <string.h>
using namespace std;
class Graph {
int V;
list<int>* adj;
public:
Graph(int V)
{
this->V = V;
adj = new list<int>[V];
}
~Graph() { delete[] adj; }
void addEdge(int u, int v)
{
adj[u].push_back(v);
adj[v].push_back(u);
}
void rmvEdge(int u, int v);
void printEulerTour();
void printEulerUtil(int s);
int DFSCount(int v, bool visited[]);
bool isValidNextEdge(int u, int v);
};
void Graph::printEulerTour()
{
int u = 0;
for (int i = 0; i < V; i++)
if (adj[i].size() & 1) {
u = i;
break;
}
printEulerUtil(u);
cout << endl;
}
void Graph::printEulerUtil(int u)
{
list<int>::iterator i;
for (i = adj[u].begin(); i != adj[u].end(); ++i) {
int v = *i;
if (v != -1 && isValidNextEdge(u, v)) {
cout << u << "-" << v << " ";
rmvEdge(u, v);
printEulerUtil(v);
}
}
}
bool Graph::isValidNextEdge(int u, int v)
{
int count = 0;
list<int>::iterator i;
for (i = adj[u].begin(); i != adj[u].end(); ++i)
if (*i != -1)
count++;
if (count == 1)
return true;
bool visited[V];
memset(visited, false, V);
int count1 = DFSCount(u, visited);
rmvEdge(u, v);
memset(visited, false, V);
int count2 = DFSCount(u, visited);
addEdge(u, v);
return (count1 > count2) ? false : true;
}
void Graph::rmvEdge(int u, int v)
{
list<int>::iterator iv
= find(adj[u].begin(), adj[u].end(), v);
*iv = -1;
list<int>::iterator iu
= find(adj[v].begin(), adj[v].end(), u);
*iu = -1;
}
int Graph::DFSCount(int v, bool visited[])
{
visited[v] = true;
int count = 1;
list<int>::iterator i;
for (i = adj[v].begin(); i != adj[v].end(); ++i)
if (*i != -1 && !visited[*i])
count += DFSCount(*i, visited);
return count;
}
int main()
{
Graph g1(4);
g1.addEdge(0, 1);
g1.addEdge(0, 2);
g1.addEdge(1, 2);
g1.addEdge(2, 3);
g1.printEulerTour();
Graph g2(3);
g2.addEdge(0, 1);
g2.addEdge(1, 2);
g2.addEdge(2, 0);
g2.printEulerTour();
Graph g3(5);
g3.addEdge(1, 0);
g3.addEdge(0, 2);
g3.addEdge(2, 1);
g3.addEdge(0, 3);
g3.addEdge(3, 4);
g3.addEdge(3, 2);
g3.addEdge(3, 1);
g3.addEdge(2, 4);
g3.printEulerTour();
return 0;
}
|
Java
import java.util.ArrayList;
public class Graph {
private int vertices;
private ArrayList<Integer>[] adj;
Graph(int numOfVertices)
{
this.vertices = numOfVertices;
initGraph();
}
@SuppressWarnings("unchecked") private void initGraph()
{
adj = new ArrayList[vertices];
for (int i = 0; i < vertices; i++) {
adj[i] = new ArrayList<>();
}
}
private void addEdge(Integer u, Integer v)
{
adj[u].add(v);
adj[v].add(u);
}
private void removeEdge(Integer u, Integer v)
{
adj[u].remove(v);
adj[v].remove(u);
}
private void printEulerTour()
{
Integer u = 0;
for (int i = 0; i < vertices; i++) {
if (adj[i].size() % 2 == 1) {
u = i;
break;
}
}
printEulerUtil(u);
System.out.println();
}
private void printEulerUtil(Integer u)
{
for (int i = 0; i < adj[u].size(); i++) {
Integer v = adj[u].get(i);
if (isValidNextEdge(u, v)) {
System.out.print(u + "-" + v + " ");
removeEdge(u, v);
printEulerUtil(v);
}
}
}
private boolean isValidNextEdge(Integer u, Integer v)
{
if (adj[u].size() == 1) {
return true;
}
boolean[] isVisited = new boolean[this.vertices];
int count1 = dfsCount(u, isVisited);
removeEdge(u, v);
isVisited = new boolean[this.vertices];
int count2 = dfsCount(u, isVisited);
addEdge(u, v);
return (count1 > count2) ? false : true;
}
private int dfsCount(Integer v, boolean[] isVisited)
{
isVisited[v] = true;
int count = 1;
for (int adj : adj[v]) {
if (!isVisited[adj]) {
count = count + dfsCount(adj, isVisited);
}
}
return count;
}
public static void main(String a[])
{
Graph g1 = new Graph(4);
g1.addEdge(0, 1);
g1.addEdge(0, 2);
g1.addEdge(1, 2);
g1.addEdge(2, 3);
g1.printEulerTour();
Graph g2 = new Graph(3);
g2.addEdge(0, 1);
g2.addEdge(1, 2);
g2.addEdge(2, 0);
g2.printEulerTour();
Graph g3 = new Graph(5);
g3.addEdge(1, 0);
g3.addEdge(0, 2);
g3.addEdge(2, 1);
g3.addEdge(0, 3);
g3.addEdge(3, 4);
g3.addEdge(3, 2);
g3.addEdge(3, 1);
g3.addEdge(2, 4);
g3.printEulerTour();
}
}
|
Python3
from collections import defaultdict
class Graph:
def __init__(self,vertices):
self.V= vertices
self.graph = defaultdict(list)
self.Time = 0
def addEdge(self,u,v):
self.graph[u].append(v)
self.graph[v].append(u)
def rmvEdge(self, u, v):
for index, key in enumerate(self.graph[u]):
if key == v:
self.graph[u].pop(index)
for index, key in enumerate(self.graph[v]):
if key == u:
self.graph[v].pop(index)
def DFSCount(self, v, visited):
count = 1
visited[v] = True
for i in self.graph[v]:
if visited[i] == False:
count = count + self.DFSCount(i, visited)
return count
def isValidNextEdge(self, u, v):
if len(self.graph[u]) == 1:
return True
else:
visited =[False]*(self.V)
count1 = self.DFSCount(u, visited)
self.rmvEdge(u, v)
visited =[False]*(self.V)
count2 = self.DFSCount(u, visited)
self.addEdge(u,v)
return False if count1 > count2 else True
def printEulerUtil(self, u):
for v in self.graph[u]:
if self.isValidNextEdge(u, v):
print("%d-%d " %(u,v)),
self.rmvEdge(u, v)
self.printEulerUtil(v)
def printEulerTour(self):
u = 0
for i in range(self.V):
if len(self.graph[i]) %2 != 0 :
u = i
break
print ("\n")
self.printEulerUtil(u)
g1 = Graph(4)
g1.addEdge(0, 1)
g1.addEdge(0, 2)
g1.addEdge(1, 2)
g1.addEdge(2, 3)
g1.printEulerTour()
g2 = Graph(3)
g2.addEdge(0, 1)
g2.addEdge(1, 2)
g2.addEdge(2, 0)
g2.printEulerTour()
g3 = Graph (5)
g3.addEdge(1, 0)
g3.addEdge(0, 2)
g3.addEdge(2, 1)
g3.addEdge(0, 3)
g3.addEdge(3, 4)
g3.addEdge(3, 2)
g3.addEdge(3, 1)
g3.addEdge(2, 4)
g3.printEulerTour()
|
C#
using System;
using System.Collections.Generic;
class Graph
{
private int vertices;
private List<int>[] adj;
Graph(int numOfVertices)
{
this.vertices = numOfVertices;
initGraph();
}
private void initGraph()
{
adj = new List<int>[vertices];
for (int i = 0; i < vertices; i++)
{
adj[i] = new List<int>();
}
}
private void addEdge(int u, int v)
{
adj[u].Add(v);
adj[v].Add(u);
}
private void removeEdge(int u, int v)
{
adj[u].Remove(v);
adj[v].Remove(u);
}
private void printEulerTour()
{
int u = 0;
for (int i = 0; i < vertices; i++)
{
if (adj[i].Count % 2 == 1)
{
u = i;
break;
}
}
printEulerUtil(u);
Console.WriteLine();
}
private void printEulerUtil(int u)
{
for (int i = 0; i < adj[u].Count; i++)
{
int v = adj[u][i];
if (isValidNextEdge(u, v))
{
Console.Write(u + "-" + v + " ");
removeEdge(u, v);
printEulerUtil(v);
}
}
}
private bool isValidNextEdge(int u, int v)
{
if (adj[u].Count == 1)
{
return true;
}
bool[] isVisited = new bool[this.vertices];
int count1 = dfsCount(u, isVisited);
removeEdge(u, v);
isVisited = new bool[this.vertices];
int count2 = dfsCount(u, isVisited);
addEdge(u, v);
return (count1 > count2) ? false : true;
}
private int dfsCount(int v, bool[] isVisited)
{
isVisited[v] = true;
int count = 1;
foreach(int i in adj[v])
{
if (!isVisited[i])
{
count = count + dfsCount(i, isVisited);
}
}
return count;
}
public static void Main(String []a)
{
Graph g1 = new Graph(4);
g1.addEdge(0, 1);
g1.addEdge(0, 2);
g1.addEdge(1, 2);
g1.addEdge(2, 3);
g1.printEulerTour();
Graph g2 = new Graph(3);
g2.addEdge(0, 1);
g2.addEdge(1, 2);
g2.addEdge(2, 0);
g2.printEulerTour();
Graph g3 = new Graph(5);
g3.addEdge(1, 0);
g3.addEdge(0, 2);
g3.addEdge(2, 1);
g3.addEdge(0, 3);
g3.addEdge(3, 4);
g3.addEdge(3, 2);
g3.addEdge(3, 1);
g3.addEdge(2, 4);
g3.printEulerTour();
}
}
|
Javascript
class Graph {
constructor(V) {
this.V = V;
this.adj = Array.from(Array(V), () => new Array());
}
addEdge(u, v) {
this.adj[u].push(v);
this.adj[v].push(u);
}
rmvEdge(u, v) {
for (let i = 0; i < this.adj[u].length; i++) {
if (this.adj[u][i] == v) {
this.adj[u][i] = -1;
break;
}
}
for (let i = 0; i < this.adj[v].length; i++) {
if (this.adj[v][i] == u) {
this.adj[v][i] = -1;
break;
}
}
}
printEulerTour() {
let u = 0;
for (let i = 0; i < this.V; i++)
if (this.adj[i].length & 1) {
u = i;
break;
}
this.printEulerUtil(u);
console.log(" ");
}
printEulerUtil(u) {
{
for (let j in this.adj[u]) {
let v = this.adj[u][j];
if (v != -1 && this.isValidNextEdge(u, v)) {
console.log(u + "-" + v);
this.rmvEdge(u, v);
this.printEulerUtil(v);
}
}
}
}
DFSCount(v, visited) {
visited[v] = true;
let count = 1;
for (let j in this.adj[v]) {
let i = this.adj[v][j];
if (i != -1 && !visited[i]) count += this.DFSCount(i, visited);
}
return count;
}
isValidNextEdge(u, v) {
let count = 0;
for (let j in this.adj[u]) {
let i = this.adj[u][j];
if (i != -1) count++;
}
if (count == 1) return true;
let visited = new Array(this.V);
visited.fill(false);
let count1 = this.DFSCount(u, visited);
this.rmvEdge(u, v);
visited.fill(false);
let count2 = this.DFSCount(u, visited);
this.addEdge(u, v);
return count1 > count2 ? false : true;
}
}
let g1 = new Graph(4);
g1.addEdge(0, 1);
g1.addEdge(0, 2);
g1.addEdge(1, 2);
g1.addEdge(2, 3);
g1.printEulerTour();
let g2 = new Graph(3);
g2.addEdge(0, 1);
g2.addEdge(1, 2);
g2.addEdge(2, 0);
g2.printEulerTour();
let g3 = new Graph(5);
g3.addEdge(1, 0);
g3.addEdge(0, 2);
g3.addEdge(2, 1);
g3.addEdge(0, 3);
g3.addEdge(3, 4);
g3.addEdge(3, 2);
g3.addEdge(3, 1);
g3.addEdge(2, 4);
g3.printEulerTour();
|
Output
2-0 0-1 1-2 2-3
0-1 1-2 2-0
0-1 1-2 2-0 0-3 3-4 4-2 2-3 3-1
Note that the above code modifies the given graph, we can create a copy of the graph if we don’t want the given graph to be modified.
Time Complexity: The time complexity of the above implementation is O ((V+E)2). The function printEulerUtil() is like DFS and it calls isValidNextEdge() which also does DFS two times. The time complexity of DFS for adjacency list representation is O(V+E). Therefore overall time complexity is O((V+E)*(V+E)) which can be written as O(E2) for a connected graph.
There are better algorithms to print Euler tour, Hierholzer’s Algorithm finds in O(V+E) time.
Space complexity: O(V+E),the space complexity of the above program is O(V+E) as we are using an adjacency list to represent the graph. The size of the adjacency list is equal to the number of vertices plus the number of edges in the graph.
Share your thoughts in the comments
Please Login to comment...