Introduction to Graph Coloring

Graph coloring refers to the problem of coloring vertices of a graph in such a way that no two adjacent vertices have the same color. This is also called the vertex coloring problem. If coloring is done using at most m colors, it is called m-coloring.

Graph Coloring

Chromatic Number:

The minimum number of colors needed to color a graph is called its chromatic number. For example, the following can be colored a minimum of 2 colors. 

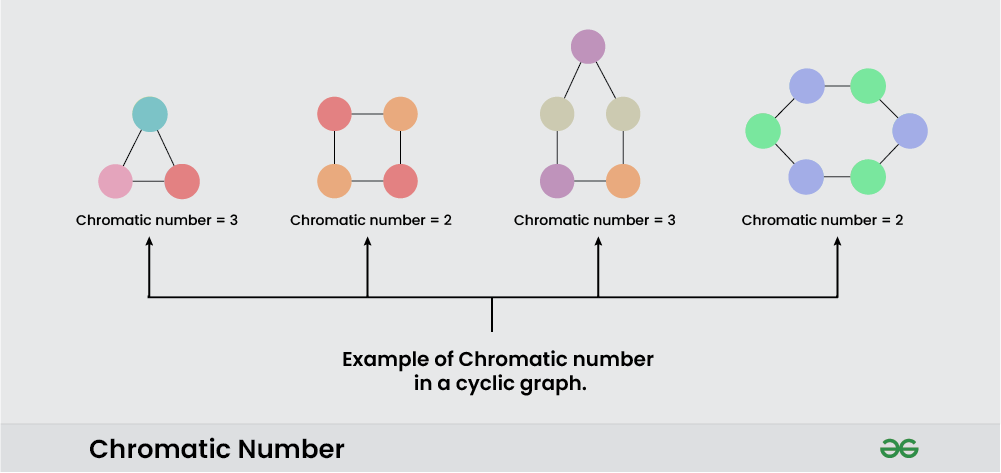
Example of Chromatic Number

The problem of finding a chromatic number of a given graph is NP-complete.

Graph coloring problem is both, a decision problem as well as an optimization problem.

• A decision problem is stated as, “With given M colors and graph G, whether a such color scheme is possible or not?”.
• The optimization problem is stated as, “Given M colors and graph G, find the minimum number of colors required for graph coloring.”

Algorithm of Graph Coloring using Backtracking:

Assign colors one by one to different vertices, starting from vertex 0. Before assigning a color, check if the adjacent vertices have the same color or not. If there is any color assignment that does not violate the conditions, mark the color assignment as part of the solution. If no assignment of color is possible then backtrack and return false.

Follow the given steps to solve the problem:

• Create a recursive function that takes the graph, current index, number of vertices, and color array.
• If the current index is equal to the number of vertices. Print the color configuration in the color array.
• Assign a color to a vertex from the range (1 to m).
  • For every assigned color, check if the configuration is safe, (i.e. check if the adjacent vertices do not have the same color) and recursively call the function with the next index and number of vertices else return false
  • If any recursive function returns true then break the loop and return true
  • If no recursive function returns true then return false

Below is the implementation of the above approach:

C++

// C++ program for solution of M
// Coloring problem using backtracking

#include <bits/stdc++.h>
using namespace std;

// Number of vertices in the graph
#define V 4

void printSolution(int color[]);

/* A utility function to check if
   the current color assignment
   is safe for vertex v i.e. checks
   whether the edge exists or not
   (i.e, graph[v][i]==1). If exist
   then checks whether the color to
   be filled in the new vertex(c is
   sent in the parameter) is already
   used by its adjacent
   vertices(i-->adj vertices) or
   not (i.e, color[i]==c) */
bool isSafe(int v, bool graph[V][V], int color[], int c)
{
    for (int i = 0; i < V; i++)
        if (graph[v][i] && c == color[i])
            return false;

    return true;
}

/* A recursive utility function
to solve m coloring problem */
bool graphColoringUtil(bool graph[V][V], int m, int color[],
                       int v)
{

    /* base case: If all vertices are
       assigned a color then return true */
    if (v == V)
        return true;

    /* Consider this vertex v and
       try different colors */
    for (int c = 1; c <= m; c++) {

        /* Check if assignment of color
           c to v is fine*/
        if (isSafe(v, graph, color, c)) {
            color[v] = c;

            /* recur to assign colors to
               rest of the vertices */
            if (graphColoringUtil(graph, m, color, v + 1)
                == true)
                return true;

            /* If assigning color c doesn't
               lead to a solution then remove it */
            color[v] = 0;
        }
    }

    /* If no color can be assigned to
       this vertex then return false */
    return false;
}

/* This function solves the m Coloring
   problem using Backtracking. It mainly
   uses graphColoringUtil() to solve the
   problem. It returns false if the m
   colors cannot be assigned, otherwise
   return true and prints assignments of
   colors to all vertices. Please note
   that there may be more than one solutions,
   this function prints one of the
   feasible solutions.*/
bool graphColoring(bool graph[V][V], int m)
{

    // Initialize all color values as 0.
    // This initialization is needed
    // correct functioning of isSafe()
    int color[V];
    for (int i = 0; i < V; i++)
        color[i] = 0;

    // Call graphColoringUtil() for vertex 0
    if (graphColoringUtil(graph, m, color, 0) == false) {
        cout << "Solution does not exist";
        return false;
    }

    // Print the solution
    printSolution(color);
    return true;
}

/* A utility function to print solution */
void printSolution(int color[])
{
    cout << "Solution Exists:"
         << " Following are the assigned colors"
         << "\n";
    for (int i = 0; i < V; i++)
        cout << " " << color[i] << " ";

    cout << "\n";
}

// Driver code
int main()
{

    /* Create following graph and test
       whether it is 3 colorable
      (3)---(2)
       |   / |
       |  /  |
       | /   |
      (0)---(1)
    */
    bool graph[V][V] = {
        { 0, 1, 1, 1 },
        { 1, 0, 1, 0 },
        { 1, 1, 0, 1 },
        { 1, 0, 1, 0 },
    };

    // Number of colors
    int m = 3;

    // Function call
    graphColoring(graph, m);
    return 0;
}

Output

Solution Exists: Following are the assigned colors
 1  2  3  2 

Applications of Graph Coloring:

• Design a timetable.
• Sudoku.
• Register allocation in the compiler.
• Map coloring.
• Mobile radio frequency assignment.