Count all possible walks from a source to a destination with exactly k edges
Last Updated :
24 Mar, 2023
Given a directed graph and two vertices ‘u’ and ‘v’ in it, count all possible walks from ‘u’ to ‘v’ with exactly k edges on the walk.
The graph is given adjacency matrix representation where the value of graph[i][j] as 1 indicates that there is an edge from vertex i to vertex j and a value 0 indicates no edge from i to j.
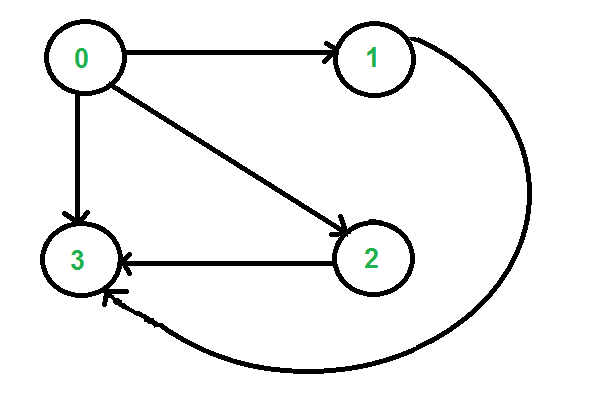
For example, consider the following graph. Let source ‘u’ be vertex 0, destination ‘v’ be 3 and k be 2. The output should be 2 as there are two walks from 0 to 3 with exactly 2 edges. The walks are {0, 2, 3} and {0, 1, 3}
Simple Approach: Create a recursive function that takes the current vertex, destination vertex, and the count of the vertex. Call the recursive function with all adjacent vertices of a current vertex with the value of k as k-1. When the value of k is 0, then check whether the current vertex is the destination or not. If destination, then the output answer is 1.
The following is the implementation of this simple solution.
C++
#include <iostream>
using namespace std;
#define V 4
int countwalks(int graph[][V], int u, int v, int k)
{
if (k == 0 && u == v)
return 1;
if (k == 1 && graph[u][v])
return 1;
if (k <= 0)
return 0;
int count = 0;
for (int i = 0; i < V; i++)
if (graph[u][i] == 1)
count += countwalks(graph, i, v, k - 1);
return count;
}
int main()
{
int graph[V][V] = { { 0, 1, 1, 1 },
{ 0, 0, 0, 1 },
{ 0, 0, 0, 1 },
{ 0, 0, 0, 0 } };
int u = 0, v = 3, k = 2;
cout << countwalks(graph, u, v, k);
return 0;
}
|
Java
import java.util.*;
import java.lang.*;
import java.io.*;
class KPaths {
static final int V = 4;
int countwalks(int graph[][], int u, int v, int k)
{
if (k == 0 && u == v)
return 1;
if (k == 1 && graph[u][v] == 1)
return 1;
if (k <= 0)
return 0;
int count = 0;
for (int i = 0; i < V; i++)
if (graph[u][i] == 1)
count += countwalks(graph, i, v, k - 1);
return count;
}
public static void main(String[] args) throws java.lang.Exception
{
int graph[][] = new int[][] { { 0, 1, 1, 1 },
{ 0, 0, 0, 1 },
{ 0, 0, 0, 1 },
{ 0, 0, 0, 0 } };
int u = 0, v = 3, k = 2;
KPaths p = new KPaths();
System.out.println(p.countwalks(graph, u, v, k));
}
}
|
Python3
V = 4
def countwalks(graph, u, v, k):
if (k == 0 and u == v):
return 1
if (k == 1 and graph[u][v]):
return 1
if (k <= 0):
return 0
count = 0
for i in range(0, V):
if (graph[u][i] == 1):
count += countwalks(graph, i, v, k-1)
return count
graph = [[0, 1, 1, 1, ],
[0, 0, 0, 1, ],
[0, 0, 0, 1, ],
[0, 0, 0, 0] ]
u = 0; v = 3; k = 2
print(countwalks(graph, u, v, k))
|
C#
using System;
class GFG {
static int V = 4;
static int countwalks(int[, ] graph, int u,
int v, int k)
{
if (k == 0 && u == v)
return 1;
if (k == 1 && graph[u, v] == 1)
return 1;
if (k <= 0)
return 0;
int count = 0;
for (int i = 0; i < V; i++)
if (graph[u, i] == 1)
count += countwalks(graph, i, v, k - 1);
return count;
}
public static void Main()
{
int[, ] graph = new int[, ] { { 0, 1, 1, 1 },
{ 0, 0, 0, 1 },
{ 0, 0, 0, 1 },
{ 0, 0, 0, 0 } };
int u = 0, v = 3, k = 2;
Console.Write(
countwalks(graph, u, v, k));
}
}
|
PHP
<?php
$V = 4;
function countwalks( $graph, $u, $v, $k)
{
global $V;
if ($k == 0 and $u == $v)
return 1;
if ($k == 1 and $graph[$u][$v])
return 1;
if ($k <= 0)
return 0;
$count = 0;
for ( $i = 0; $i < $V; $i++)
if ($graph[$u][$i] == 1)
$count += countwalks($graph, $i,
$v, $k - 1);
return $count;
}
$graph = array(array(0, 1, 1, 1),
array(0, 0, 0, 1),
array(0, 0, 0, 1),
array(0, 0, 0, 0));
$u = 0; $v = 3; $k = 2;
echo countwalks($graph, $u, $v, $k);
?>
|
Javascript
<script>
var V = 4
function countwalks(graph, u, v, k)
{
if (k == 0 && u == v)
return 1;
if (k == 1 && graph[u][v])
return 1;
if (k <= 0)
return 0;
var count = 0;
for (var i = 0; i < V; i++)
if (graph[u][i] == 1)
count += countwalks(graph, i, v, k - 1);
return count;
}
var graph = [[0, 1, 1, 1, ],
[0, 0, 0, 1, ],
[0, 0, 0, 1, ],
[0, 0, 0, 0] ];
var u = 0, v = 3, k = 2;
document.write(countwalks(graph, u, v, k));
</script>
|
Complexity Analysis:
- Time Complexity: O(Vk).
The worst-case time complexity of the above function is O(Vk) where V is the number of vertices in the given graph. We can simply analyze the time complexity by drawing a recursion tree. The worst occurs for a complete graph. In the worst case, every internal node of the recursion tree would have exactly n children.
- Auxiliary Space: O(V).
To store the stack space and the visited array O(V) space is needed.
Efficient Approach: The solution can be optimized using Dynamic Programming. The idea is to build a 3D table where the first dimension is the source, the second dimension is the destination, the third dimension is the number of edges from source to destination, and the value is the count of walks. Like others, Dynamic Programming problems, fill the 3D table in a bottom-up manner.
C++
#include <iostream>
using namespace std;
#define V 4
int countwalks(int graph[][V], int u, int v, int k)
{
int count[V][V][k + 1];
for (int e = 0; e <= k; e++) {
for (int i = 0; i < V; i++)
{
for (int j = 0; j < V; j++)
{
count[i][j][e] = 0;
if (e == 0 && i == j)
count[i][j][e] = 1;
if (e == 1 && graph[i][j])
count[i][j][e] = 1;
if (e > 1) {
for (int a = 0; a < V; a++)
if (graph[i][a])
count[i][j][e] += count[a][j][e - 1];
}
}
}
}
return count[u][v][k];
}
int main()
{
int graph[V][V] = { { 0, 1, 1, 1 },
{ 0, 0, 0, 1 },
{ 0, 0, 0, 1 },
{ 0, 0, 0, 0 } };
int u = 0, v = 3, k = 2;
cout << countwalks(graph, u, v, k);
return 0;
}
|
Java
import java.util.*;
import java.lang.*;
import java.io.*;
class KPaths {
static final int V = 4;
int countwalks(int graph[][], int u, int v, int k)
{
int count[][][] = new int[V][V][k + 1];
for (int e = 0; e <= k; e++) {
for (int i = 0; i < V; i++)
{
for (int j = 0; j < V; j++)
{
count[i][j][e] = 0;
if (e == 0 && i == j)
count[i][j][e] = 1;
if (e == 1 && graph[i][j] != 0)
count[i][j][e] = 1;
if (e > 1) {
for (int a = 0; a < V; a++)
if (graph[i][a] != 0)
count[i][j][e] += count[a][j][e - 1];
}
}
}
}
return count[u][v][k];
}
public static void main(String[] args) throws java.lang.Exception
{
int graph[][] = new int[][] { { 0, 1, 1, 1 },
{ 0, 0, 0, 1 },
{ 0, 0, 0, 1 },
{ 0, 0, 0, 0 } };
int u = 0, v = 3, k = 2;
KPaths p = new KPaths();
System.out.println(p.countwalks(graph, u, v, k));
}
}
|
Python3
V = 4
def countwalks(graph, u, v, k):
count = [[[0 for k in range(k + 1)]
for i in range(V)]
for j in range(V)]
for e in range(0, k + 1):
for i in range(V):
for j in range(V):
if (e == 0 and i == j):
count[i][j][e] = 1
if (e == 1 and graph[i][j] != 0):
count[i][j][e] = 1
if (e > 1):
for a in range(V):
if (graph[i][a] != 0):
count[i][j][e] += count[a][j][e - 1]
return count[u][v][k]
if __name__ == '__main__':
graph = [[0, 1, 1, 1],
[0, 0, 0, 1],
[0, 0, 0, 1],
[0, 0, 0, 0]]
u = 0
v = 3
k = 2
print(countwalks(graph, u, v, k))
|
C#
using System;
class GFG {
static int V = 4;
static int countwalks(int[, ] graph, int u,
int v, int k)
{
int[,, ] count = new int[V, V, k + 1];
for (int e = 0; e <= k; e++) {
for (int i = 0; i < V; i++) {
for (int j = 0; j < V; j++) {
count[i, j, e] = 0;
if (e == 0 && i == j)
count[i, j, e] = 1;
if (e == 1 && graph[i, j] != 0)
count[i, j, e] = 1;
if (e > 1) {
for (int a = 0; a < V; a++)
if (graph[i, a] != 0)
count[i, j, e] += count[a, j, e - 1];
}
}
}
}
return count[u, v, k];
}
public static void Main()
{
int[, ] graph = { { 0, 1, 1, 1 },
{ 0, 0, 0, 1 },
{ 0, 0, 0, 1 },
{ 0, 0, 0, 0 } };
int u = 0, v = 3, k = 2;
Console.WriteLine(
countwalks(graph, u, v, k));
}
}
|
Javascript
<script>
var V = 4
function countwalks(graph, u, v, k)
{
var count = new Array(V);
for (var i = 0; i <V; i++) {
count[i] = new Array(V);
for (var j = 0; j < V; j++) {
count[i][j] = new Array(V);
for (var e = 0; e <= k; e++) {
count[i][j][e] = 0;
}
}
}
for (var e = 0; e <= k; e++) {
for (var i = 0; i < V; i++)
{
for (var j = 0; j < V; j++)
{
count[i][j][e] = 0;
if (e == 0 && i == j)
count[i][j][e] = 1;
if (e == 1 && graph[i][j])
count[i][j][e] = 1;
if (e > 1) {
for (var a = 0; a < V; a++)
if (graph[i][a])
count[i][j][e] += count[a][j][e - 1];
}
}
}
}
return count[u][v][k];
}
var graph = [ [ 0, 1, 1, 1 ],
[ 0, 0, 0, 1 ],
[ 0, 0, 0, 1 ],
[ 0, 0, 0, 0 ] ];
var u = 0, v = 3, k = 2;
document.write(countwalks(graph, u, v, k));
</script>
|
PHP
<?php
define('V', 4);
function countwalks($graph, $u, $v, $k)
{
$count = array();
for ($i = 0; $i < V; $i++) {
for ($j = 0; $j < V; $j++) {
for ($e = 0; $e <= $k; $e++) {
$count[$i][$j][$e] = 0;
}
}
}
for ($e = 0; $e <= $k; $e++) {
for ($i = 0; $i < V; $i++)
{
for ($j = 0; $j < V; $j++)
{
$count[$i][$j][$e] = 0;
if ($e == 0 && $i == $j)
$count[$i][$j][$e] = 1;
if ($e == 1 && $graph[$i][$j])
$count[$i][$j][$e] = 1;
if ($e > 1) {
for ($a = 0; $a < V; $a++)
if ($graph[$i][$a])
$count[$i][$j][$e] += $count[$a][$j][$e - 1];
}
}
}
}
return $count[$u][$v][$k];
}
$graph = array(array(0, 1, 1, 1),
array(0, 0, 0, 1),
array(0, 0, 0, 1),
array(0, 0, 0, 0));
$u = 0;
$v = 3;
$k = 2;
echo countwalks($graph, $u, $v, $k);
?>
|
Complexity Analysis:
- Time Complexity: O(V3).
Three nested loops are needed to fill the DP table, so the time complexity is O(V3).
- Auxiliary Space: O(V2K).
To store the DP table O(V2K) space is needed.
We can also use Divide and Conquer to solve the above problem in O(V3Logk) time. The count of walks of length k from u to v is the [u][v]’th entry in (graph[V][V])k. We can calculate the power by doing O(Logk) multiplication by using the divide and conquer technique to calculate power. A multiplication between two matrices of size V x V takes O(V3) time.
Share your thoughts in the comments
Please Login to comment...